C語(yǔ)言中要求平方根,可以在頭文件中加入#include 《math.h》。然后調(diào)用sqrt(n);函數(shù)即可。但在單片機(jī)中調(diào)用此函數(shù)無(wú)疑會(huì)耗費(fèi)大量資源和時(shí)間,是極不合適的。在此,總結(jié)下網(wǎng)上常見(jiàn)的四種單片機(jī)常用開(kāi)方根算法:
對(duì)于擁有專(zhuān)門(mén)的乘除法指令的單片機(jī),可采用以下兩種方法:
1、二分法
對(duì)于一個(gè)非負(fù)數(shù)n,它的平方根不會(huì)小于大于(n/2+1)(謝謝@linzhi-cs提醒)。在[0, n/2+1]這個(gè)范圍內(nèi)可以進(jìn)行二分搜索,求出n的平方根。
-------------------------------------------------------------------------------
1 int sqrt(int x) { 2 long long i = 0; 3 long long j = x / 2 + 1; 4 while (i 《= j) 5 { 6 long long mid = (i + j) / 2; 7 long long sq = mid * mid; 8 if (sq == x) return mid; 9 else if (sq 《 x) i = mid + 1;10 else j = mid - 1;11 }12 return j;13 }
-------------------------------------------------------------------------------
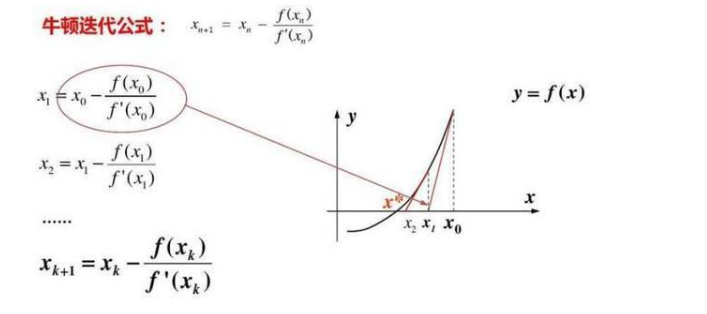
2、更為常用的牛頓迭代法
-------------------------------------------------------------------------------
1 int sqrt(int x) { 2 if (x == 0) return 0; 3 double last = 0; 4 double res = 1; 5 while (res != last) 6 { 7 last = res; 8 res = (res + x / res) / 2; 9 }10 return int(res);11 }
-------------------------------------------------------------------------------
牛頓迭代法也可以求解多次方程。
對(duì)于不帶乘除法指令的單片機(jī),可采取以下兩種算法:
算法3:
本算法只采用移位、加減法、判斷和循環(huán)實(shí)現(xiàn),因?yàn)樗恍枰↑c(diǎn)運(yùn)算,也不需要乘除運(yùn)算,因此可以很方便地運(yùn)用到各種芯片上去。
我們先來(lái)看看10進(jìn)制下是如何手工計(jì)算開(kāi)方的:
先看下面兩個(gè)算式:
x = 10*p + q (1)
公式(1)左右平方之后得:
x^2 = 100*p^2 + 20pq + q^2 (2)
現(xiàn)在假設(shè)我們知道x^2和p,希望求出q來(lái),求出了q也就求出了x^2的開(kāi)方x了。
我們把公式(2)改寫(xiě)為如下格式:
q = (x^2 - 100*p^2)/(20*p+q) (3)
這個(gè)算式左右都有q,因此無(wú)法直接計(jì)算出q來(lái),因此手工的開(kāi)方算法和手工除法算法一樣有一步需要猜值。
我們來(lái)一個(gè)手工計(jì)算的例子:計(jì)算1234567890的開(kāi)方
首先我們把這個(gè)數(shù)兩位兩位一組分開(kāi),計(jì)算出最高位為3。也就是(3)中的p,最下面一行的334為余數(shù),也就是公式(3)中的(x^2 - 100*p^2)近似值
3 --------------- | 12 34 56 78 90 9 --------------- | 3 34
下面我們要找到一個(gè)0-9的數(shù)q使它最接近滿足公式(3)。我們先把p乘以20寫(xiě)在334左邊:
3 q --------------- | 12 34 56 78 90 9 --------------- 6q| 3 34
我們看到q為5時(shí)(60+q*q)的值最接近334,而且不超過(guò)334。于是我們得到:
3 5 --------------- | 12 34 56 78 90 9 --------------- 65| 3 34 | 3 25 --------------- 9 56
接下來(lái)就是重復(fù)上面的步驟了,這里就不再啰嗦了。
這個(gè)手工算法其實(shí)和10進(jìn)制關(guān)系不大,因此我們可以很容易的把它改為二進(jìn)制,改為二進(jìn)制之后,公式(3)就變成了:
q = (x^2 - 4*p^2)/(4*p+q) (4)
我們來(lái)看一個(gè)例子,計(jì)算100(二進(jìn)制1100100)的開(kāi)方:
1 0 1 0 --------------- | 1 10 01 00 1 --------------- 100| 0 10 | 0 00 --------------- | 10 011001| 10 01 --------------- 0 00
這里每一步不再是把p乘以20了,而是把p乘以4,也就是把p右移兩位,而由于q的值只能為0或者1,所以我們只需要判斷余數(shù)(x^2 - 4*p^2)和(4*p+1)的大小關(guān)系,如果余數(shù)大于等于(4*p+q)那么該上一個(gè)1,否則該上一個(gè)0。
下面給出完成的C語(yǔ)言程序,其中root表示p,rem表示每步計(jì)算之后的余數(shù),divisor表示(4*p+1),通過(guò)a》》30取a的最高 2位,通過(guò)a《《=2將計(jì)算后的最高2位剔除。其中root的兩次《《1相當(dāng)于4*p。程序完全是按照手工計(jì)算改寫(xiě)的,應(yīng)該不難理解。
-------------------------------------------------------------------------------
unsigned short sqrt(unsigned long a){ unsigned long rem = 0; unsigned long root = 0; unsigned long divisor = 0; for(int i=0; i《16; i++){ root 《《= 1; rem = ((rem 《《 2) + (a 》》 30)); a 《《= 2; divisor = (root《《1) + 1; if(divisor 《= rem){ rem -= divisor; root++; } } return (unsigned short)(root); }
-------------------------------------------------------------------------------
算法4
這種方法比牛頓迭代法更加快速的方法。
1.原理
下述用pow(X,Y)表示X的Y次冪,用B[0],B[1],。。。,B[m-1]表示一個(gè)序列,
其中[x]為下標(biāo)。
假設(shè):
B[x],b[x]都是二進(jìn)制序列,取值0或1。
1、 M = B[m-1]*pow(2,m-1) + B[m-2]*pow(2,m-2) + 。。。 + B[1]*pow(2,1) + B[0]*pow
(2,0)
2、 N = b[n-1]*pow(2,n-1) + b[n-2]*pow(2,n-2) + 。。。 + b[1]*pow(2,1) + n[0]*pow
(2,0)
3、 pow(N,2) = M
(1) N的最高位b[n-1]可以根據(jù)M的最高位B[m-1]直接求得。
設(shè) m 已知,因?yàn)?pow(2, m-1) 《= M 《= pow(2, m),所以 pow(2, (m-1)/2) 《= N 《=
pow(2, m/2)
如果 m 是奇數(shù),設(shè)m=2*k+1,
那么 pow(2,k) 《= N 《 pow(2, 1/2+k) 《 pow(2, k+1),
n-1=k, n=k+1=(m+1)/2
如果 m 是偶數(shù),設(shè)m=2k,
那么 pow(2,k) 》 N 》= pow(2, k-1/2) 》 pow(2, k-1),
n-1=k-1,n=k=m/2
所以b[n-1]完全由B[m-1]決定。
余數(shù) M[1] = M - b[n-1]*pow(2, 2*n-2)
(2) N的次高位b[n-2]可以采用試探法來(lái)確定。
因?yàn)閎[n-1]=1,假設(shè)b[n-2]=1,則 pow(b[n-1]*pow(2,n-1) + b[n-1]*pow(2,n-2),
2) = b[n-1]*pow(2,2*n-2) + (b[n-1]*pow(2,2*n-2) + b[n-2]*pow(2,2*n-4)),
然后比較余數(shù)M[1]是否大于等于 (pow(2,2)*b[n-1] + b[n-2]) * pow(2,2*n-4)。這種
比較只須根據(jù)B[m-1]、B[m-2]、。。。、B[2*n-4]便可做出判斷,其余低位不做比較。
若 M[1] 》= (pow(2,2)*b[n-1] + b[n-2]) * pow(2,2*n-4), 則假設(shè)有效,b[n-2] =
1;
余數(shù) M[2] = M[1] - pow(pow(2,n-1)*b[n-1] + pow(2,n-2)*b[n-2], 2) = M[1] -
(pow(2,2)+1)*pow(2,2*n-4);
若 M[1] 《 (pow(2,2)*b[n-1] + b[n-2]) * pow(2,2*n-4), 則假設(shè)無(wú)效,b[n-2] =
0;余數(shù) M[2] = M[1]。
(3) 同理,可以從高位到低位逐位求出M的平方根N的各位。
使用這種算法計(jì)算32位數(shù)的平方根時(shí)最多只須比較16次,而且每次比較時(shí)不必把M的各位逐
一比較,尤其是開(kāi)始時(shí)比較的位數(shù)很少,所以消耗的時(shí)間遠(yuǎn)低于牛頓迭代法。
2. 實(shí)現(xiàn)代碼
這里給出實(shí)現(xiàn)32位無(wú)符號(hào)整數(shù)開(kāi)方得到16位無(wú)符號(hào)整數(shù)的C語(yǔ)言代碼。
-------------------------------------------------------------------------------
/****************************************/ /*Function: 開(kāi)根號(hào)處理 */ /*入口參數(shù):被開(kāi)方數(shù),長(zhǎng)整型 */ /*出口參數(shù):開(kāi)方結(jié)果,整型 */ /****************************************/ unsigned int sqrt_16(unsigned long M) { unsigned int N, i; unsigned long tmp, ttp; // 結(jié)果、循環(huán)計(jì)數(shù) if (M == 0) // 被開(kāi)方數(shù),開(kāi)方結(jié)果也為0 return 0; N = 0; tmp = (M 》》 30); // 獲取最高位:B[m-1] M 《《= 2; if (tmp 》 1) // 最高位為1 { N ++; // 結(jié)果當(dāng)前位為1,否則為默認(rèn)的0 tmp -= N; } for (i=15; i》0; i--) // 求剩余的15位 { N 《《= 1; // 左移一位 tmp 《《= 2; tmp += (M 》》 30); // 假設(shè) ttp = N; ttp = (ttp《《1)+1; M 《《= 2; if (tmp 》= ttp) // 假設(shè)成立 { tmp -= ttp; N ++; } } return N; }
-------------------------------------------------------------------------------
以上算法結(jié)尾網(wǎng)上收集所得,雖然原理可能比較難懂,但都可在單片機(jī)中實(shí)際運(yùn)用。
責(zé)任編輯人:CC
-
單片機(jī)
+關(guān)注
關(guān)注
6057文章
44811瀏覽量
644322 -
C語(yǔ)言
+關(guān)注
關(guān)注
180文章
7626瀏覽量
139597
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
dsp,單片機(jī),pcld,fpja,這四種集成電路的各種應(yīng)用
常見(jiàn)的四種單片機(jī)常用開(kāi)方根算法
51單片機(jī)的四種串行口工作模式怎么設(shè)置
單片機(jī)的四種燒寫(xiě)方式是什么
單片機(jī)四種輸入模式
詳解單片機(jī)的四種燒寫(xiě)方式
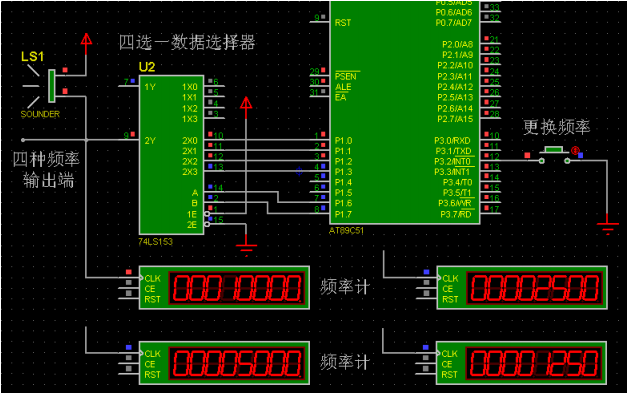
使用51單片機(jī)做信號(hào)發(fā)生器輸出四種頻率的方波的電路和程序免費(fèi)下載
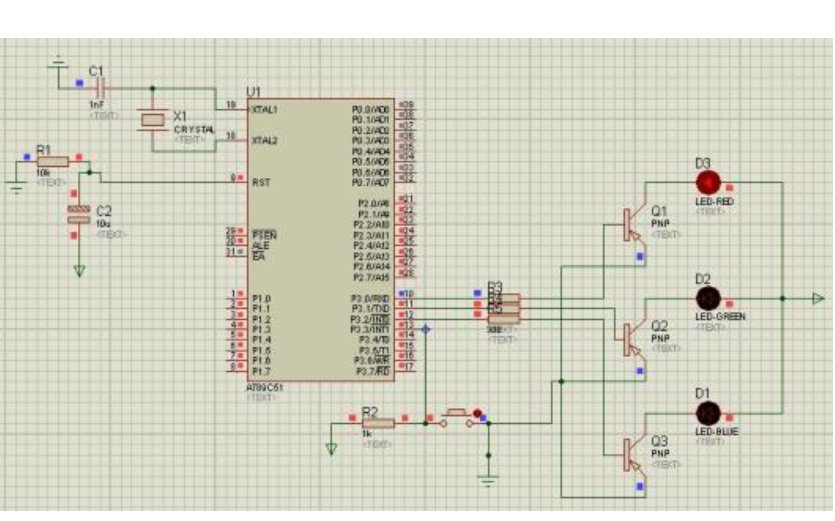
使用單片機(jī)四種方法實(shí)現(xiàn)的LED閃燈程序資料免費(fèi)下載
四種常見(jiàn)的圖像濾波算法介紹
四種單片機(jī)按鍵設(shè)計(jì)方案

單片機(jī)課設(shè)基于51單片機(jī)的波形發(fā)生器(公開(kāi)資源)(四種波形)(同時(shí)輸出兩種波形)

基于單片機(jī)四種波形發(fā)生器仿真設(shè)計(jì)-畢設(shè)課設(shè)

單片機(jī)的四種燒寫(xiě)方式

JTAG/SWD/ISP/SWIM詳解單片機(jī)的四種燒寫(xiě)方式






 常見(jiàn)的四種單片機(jī)開(kāi)方根算法分享
常見(jiàn)的四種單片機(jī)開(kāi)方根算法分享










評(píng)論