在實(shí)際環(huán)境中相干信號(hào)源是普遍存在的,如信號(hào)傳輸過程中的多徑現(xiàn)象,或者敵方有意設(shè)置的電磁干擾等。相干信號(hào)源的檢測(cè)與估計(jì)是空間譜估計(jì)中一個(gè)重要的研究方向,因此這里介紹一下相干信號(hào)源的數(shù)學(xué)模型。相干信號(hào)與非相干信號(hào)模型如下圖所示。

圖源自網(wǎng)絡(luò)
當(dāng)考察多個(gè)信號(hào)時(shí),這些信號(hào)之間可以是不相關(guān)的、相關(guān)的或相干的。對(duì)兩個(gè)平穩(wěn)信號(hào) 和 ,定義它們的相關(guān)系數(shù)為
由 Schwartz 不等式可知 ,因此,信號(hào)之間的相關(guān)性定義如下
獨(dú)立相關(guān)相干由上面的定義可知,當(dāng)信號(hào)源相干時(shí)其數(shù)學(xué)表現(xiàn)為:相干信號(hào)源間只差一個(gè)復(fù)常數(shù),假設(shè)有 個(gè)相干源,即
這里 可以稱為生成信源,因?yàn)樗闪巳肷涞疥嚵猩系?個(gè)相干信號(hào)源。則可得相干信號(hào)源模型
式中, 是由一系列復(fù)常數(shù)組成的 維矢量。
由前面的討論可知,MUSIC 算法在理想條件下具有良好的性能,但在信號(hào)源相干時(shí)算法的性能變得很壞。為什么信號(hào)源相干對(duì)算法的性能有這么大的影響呢?
當(dāng)信號(hào)源完全相干時(shí),陣列接收的數(shù)據(jù)協(xié)方差矩陣的秩降為 ,顯然這就會(huì)導(dǎo)致信號(hào)子空間的維數(shù)小于信號(hào)源數(shù)。也就是說(shuō)信號(hào)子空間“擴(kuò)散”到了噪聲子空間,這會(huì)導(dǎo)致某些相干源的導(dǎo)向矢量與噪聲子空間不完全正交,從而無(wú)法正確估計(jì)信號(hào)源方向。
由上面的分析可知:在相干信號(hào)源情況下正確估計(jì)信號(hào)方向(即解相干或去相關(guān))的核心問題是如何通過一系列處理或變換使得信號(hào)協(xié)方差矩陣的秩得到有效恢復(fù),從而正確估計(jì)信號(hào)源的方向。目前關(guān)于解相干的處理基本有兩大類:一類是降維處理;另一類是非降維處理。
降維處理算法
降維處理算法是一類常用的解相干處理方法,可以分為基于空間平滑、基于矩陣重構(gòu)兩類算法。
其中,基于空間平滑的算法主要有前向空間平滑算法、雙向空間平滑算法、修正的空間平滑算法及空域?yàn)V波法等;基于矩陣重構(gòu)的算法主要是指矩陣分解算法及矢量奇異值法等。
空間平滑類算法和矩陣重構(gòu)類算法區(qū)別在于矩陣重構(gòu)類算法修正后的協(xié)方差矩陣是長(zhǎng)方陣(估計(jì)信號(hào)子空間與噪聲子空間需用奇異值分解),而空間平滑算法修正后的矩陣是方陣(估計(jì)信號(hào)子空間與噪聲子空間可以用特征值分解)。
非降維處理算法
非降維處理算法也是一類重要的解相干處理方法,如頻域平滑算法、Toeplitz方法、虛擬陣列變換法等。這類算法與降維算法相比最大的優(yōu)點(diǎn)在于陣列孔徑?jīng)]有損失,但這類算法往往針對(duì)的是特定環(huán)境,如寬帶信號(hào)、非等距陣列、移動(dòng)陣列等。本期我們將首先討論空間平滑類算法。
空間平滑算法
眾所周知,空間平滑算法是針對(duì)一般超分辨算法不能解相干而提出的一種有效方法,它在一般情況下只適合于均勻線陣(ULA)。下面簡(jiǎn)要介紹空間平滑 MUSIC 利用子陣平滑恢復(fù)數(shù)據(jù)協(xié)方差矩陣的原理,然后深入討論加權(quán)空間平滑算法的思想。
空間平滑算法的原理
對(duì)于一窄帶情況下的均勻線陣,第 個(gè)陣元接收的數(shù)據(jù)為
式中, , , 為陣元數(shù), 為信號(hào)源數(shù)。其中, 為均勻線陣的間距, 為信號(hào)傳播速度。對(duì)于均勻線陣,令 。
空間前向平滑技術(shù)的原理如下圖所示,將均勻線陣( 個(gè)陣元)分成相互交錯(cuò)的 個(gè)子陣,每個(gè)子陣的陣元數(shù)為 ,即有 。
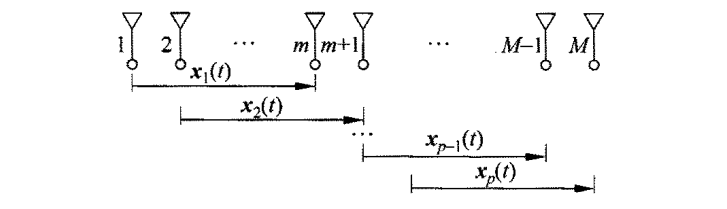
如上圖所示,取第一個(gè)子陣(一般為最左邊子陣)為參考子陣,則對(duì)于第 個(gè)子陣數(shù)據(jù)模型
式中, 為子陣導(dǎo)向矢量陣。其中
于是該子陣數(shù)據(jù)協(xié)方差矩陣為
前向空間平滑 MUSIC 方法對(duì)滿秩協(xié)方差矩陣的恢復(fù)是通過求各子陣協(xié)方差矩陣的均值來(lái)實(shí)現(xiàn)的,即取前向平滑修正的協(xié)方差矩陣為
其中, 。
注:如果子陣陣元數(shù)目 ,則當(dāng)子陣個(gè)數(shù) 時(shí)前向空間平滑數(shù)據(jù)協(xié)方差矩陣 是滿秩的。
如果按下圖劃分子陣,即采用后向平滑的方法劃分子陣。
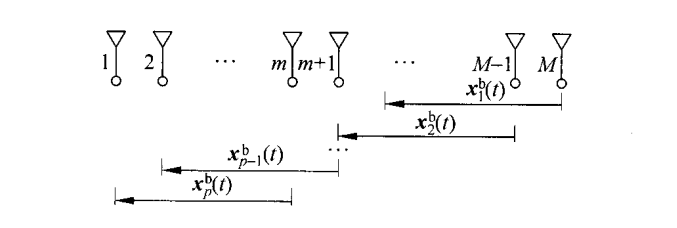
則第 個(gè)子陣的數(shù)據(jù)矢量
比較該式和前向空間平滑子陣數(shù)據(jù)模型式可得,前向第 個(gè)子陣與后向第 個(gè)子陣存在如下關(guān)系:
其中, 為 維的交換矩陣。
所以后向平滑第 個(gè)子陣的數(shù)據(jù)協(xié)方差矩陣為
又因?yàn)?/p>
所以
則后向空間平滑修正的數(shù)據(jù)矩陣為
其中, 。對(duì)于上述的后向空間平滑算法,同樣可得出如下定理。
如果子陣陣元數(shù)目 ,則當(dāng)子陣個(gè)數(shù) 時(shí)后向空間平滑數(shù)據(jù)協(xié)方差矩陣 是滿秩的。
上面是從各子陣的數(shù)據(jù)協(xié)方差矩陣角度出發(fā)得出的結(jié)論,下面換一個(gè)角度來(lái)考慮上述的空間平滑算法。定義如下兩個(gè) 數(shù)據(jù)矩陣
其中, 是反對(duì)角線為 的置換矩陣。
通過上面的定義發(fā)現(xiàn)前向平滑及后向平滑的子陣數(shù)據(jù)模型可以分別變?yōu)橐韵聝墒剑?/p>
可得到它們的協(xié)方差矩陣
則前后向平滑修正后的數(shù)據(jù)協(xié)方差矩陣可以用以下兩式表達(dá)
仔細(xì)分析以上兩式。考慮前后向空間平滑算法中的第 個(gè)子陣的數(shù)據(jù)協(xié)方差矩陣式 及式 在原始數(shù)據(jù)協(xié)方差矩陣 中的位置,可以看出, 相當(dāng)于矩陣 中第 行(列)到第 行(列)的一個(gè)子陣,而 與 滿足下列關(guān)系:
將整個(gè)數(shù)據(jù)協(xié)方差矩陣 分為如下圖所示的 個(gè)相互重疊的子陣,子陣的維數(shù)都是 ,圖中的 相當(dāng)于矩陣 中第 行到第 行及第 列到第 列的一個(gè)子陣,即 。
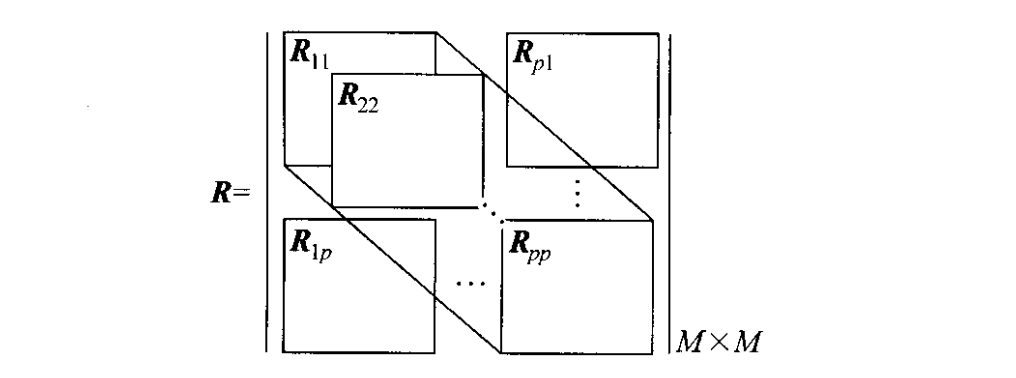
前向平滑的第 個(gè)子陣的協(xié)方差矩陣 就相當(dāng)于上圖中整個(gè)數(shù)據(jù)協(xié)方差矩陣 的第 行 第 列 分塊陣 ,而后向平滑子陣的數(shù)據(jù)協(xié)方差矩陣 只不過是對(duì) 的一種處理。即前、后向空間平滑的修正矩陣可以簡(jiǎn)化成下式:
從上述分析中可知,前后向空間平滑算法只利用了 的對(duì)角線上的分塊陣 (即各子陣的自相關(guān)信息)的平均,而沒有利用 的非對(duì)角線上的分塊陣 (各子陣間的互相關(guān)信息,其中 )。
加權(quán)空間平滑算法
通過上面的討論,可以發(fā)現(xiàn)常規(guī)的空間平滑算法的原理就是利用原始數(shù)據(jù)協(xié)方差矩陣的各對(duì)角子陣信息(子陣的自相關(guān)信息)實(shí)現(xiàn)解相干,沒有利用各子陣間的互相關(guān)信息。很顯然,對(duì)于大陣列小子陣陣元數(shù)的情況,整個(gè)數(shù)據(jù)矩陣的信息會(huì)有很大的損失,不可避免導(dǎo)致算法性能的下降。
為此,提出一種充分利用陣列所有子陣的互相關(guān)及自相關(guān)信息的方法加權(quán)空間平滑算法。下面詳細(xì)分析這一算法,該算法的協(xié)方差矩陣由下式構(gòu)成:
式中, , 均是一個(gè) 的加權(quán)矩陣, 為前向加權(quán)的修正矩陣, 為后向加權(quán)的修正矩陣。上面算法的實(shí)質(zhì)就是對(duì)數(shù)據(jù)協(xié)方差矩陣的各子陣進(jìn)行加權(quán)求和,從而實(shí)現(xiàn)對(duì)相干信號(hào)源的解相干。
該式可以看成是空間平滑算法的統(tǒng)一框架,不同的前后向加權(quán)矩陣可以得到不同的空間平滑算法。下面列舉加權(quán)空間平滑算法的幾個(gè)特例。
(1)當(dāng)前向平滑權(quán)矩陣 ,而后向平滑權(quán)矩陣 ,且 時(shí)
該式即為前面介紹的常規(guī)前向空間平滑(SS)算法。
(2)當(dāng)前向平滑權(quán)矩陣 ,而后向平滑權(quán)矩陣 ,且 時(shí)
該式即是前面介紹的后向空間平滑算法。
(3)當(dāng)前向平滑權(quán)矩陣 ,面后向平滑權(quán)矩陣 ,且 時(shí)
該式即是修正的空間平滑(MSS)算法,通常也稱為雙向平滑算法,其實(shí)質(zhì)就是前向平滑修正矩陣式與后向平滑修正矩陣式的平均。
對(duì)于雙向空間平滑算法,如果子陣陣元數(shù)目 ,則當(dāng) ,且取最優(yōu)權(quán)時(shí)的雙向加權(quán)空間平滑能保證數(shù)據(jù)協(xié)方差矩陣 是滿秩的。
由前面分析可知,單向的空間平滑 MUSIC 算法需要有 個(gè)子陣恢復(fù)滿秩協(xié)方差矩陣,而雙向空間平滑 MUSIC 算法只需要 個(gè)子陣恢復(fù)滿秩協(xié)方差矩陣,因此與單向空間平滑相比,雙向平滑陣列孔徑損失小。
事實(shí)上,當(dāng)有 個(gè)信源、每個(gè)子陣的陣元數(shù)為 時(shí),要分辨這些信源,雙向平滑共需 個(gè)陣元,而單向平滑卻至少需要 個(gè)陣元。因此當(dāng)陣元數(shù)定時(shí)(共 個(gè)陣元),前向平滑最多可分辨 個(gè)相干信源,而雙向平滑技術(shù)則可以分辨 個(gè)相干信源。
空間平滑的 MUSIC 算法及其仿真分析
通過上面的分析可知,空間平滑的 MUSIC 算法之間的不同點(diǎn)在于得到修正協(xié)方差矩陣的方法不同,但它們的目的都是為了通過空間平滑處理實(shí)現(xiàn)解相干。
下面,我們總結(jié)基于空間平滑的 MUSIC 算法的計(jì)算過程。
由陣列的接收數(shù)據(jù)得到數(shù)據(jù)協(xié)方差矩陣
利用上述介紹的方法對(duì) 進(jìn)行修正
利用修正的協(xié)方差矩陣進(jìn)行 MUSIC 譜估計(jì),找出極大值對(duì)應(yīng)的信號(hào)方向
空間平滑算法的實(shí)質(zhì)是對(duì)數(shù)據(jù)協(xié)方差矩陣的秩進(jìn)行恢復(fù)的過程,但這個(gè)過程通常只適用于等距均勻線陣,而且修正后矩陣的維數(shù)小于原矩陣的維數(shù),也就是說(shuō)解相干性能是通過降低自由度換取的。
下面為在 信噪比條件下, 個(gè)相干信號(hào)源分別從 入射時(shí)傳統(tǒng) MUSIC 算法的成像效果以及空間平滑的 MUSIC 成像效果。其中,陣列天線數(shù) ,平滑階數(shù) 。
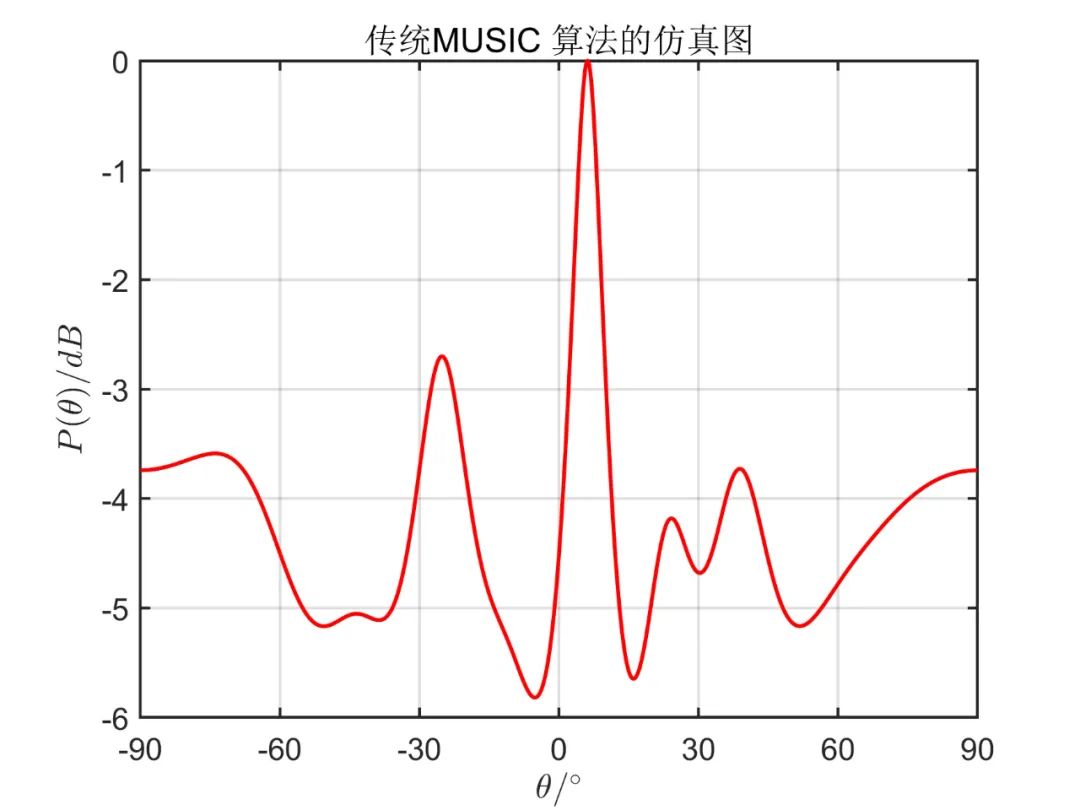
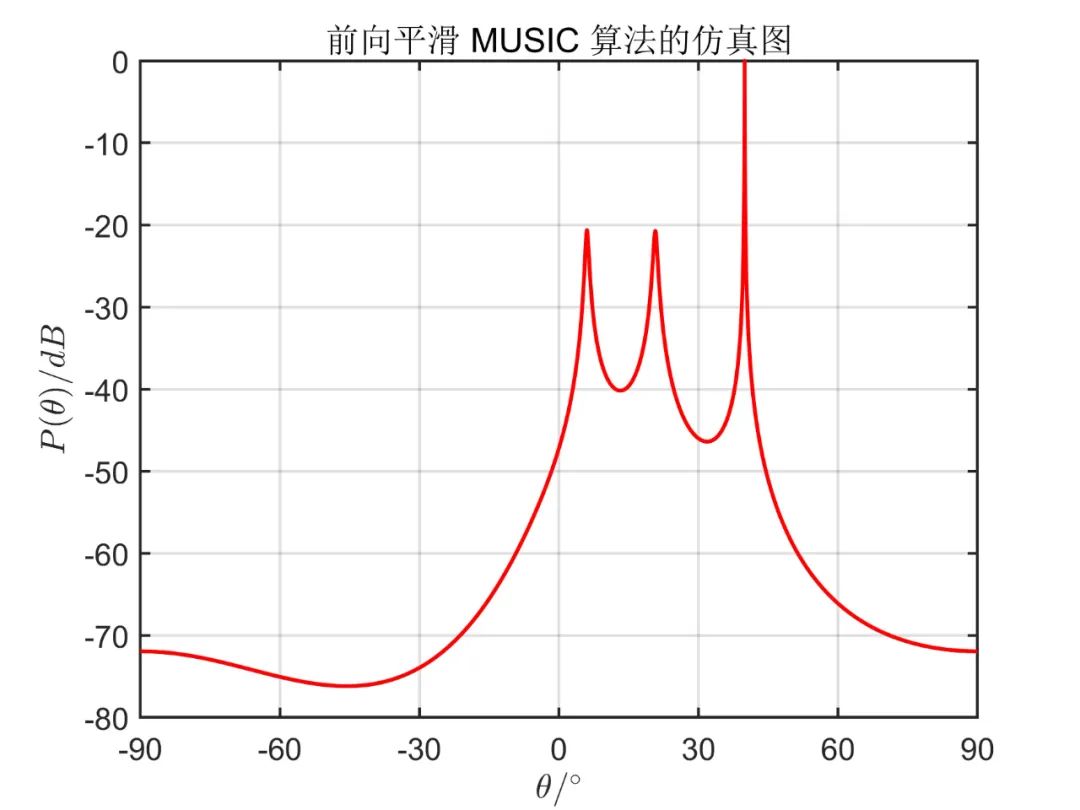
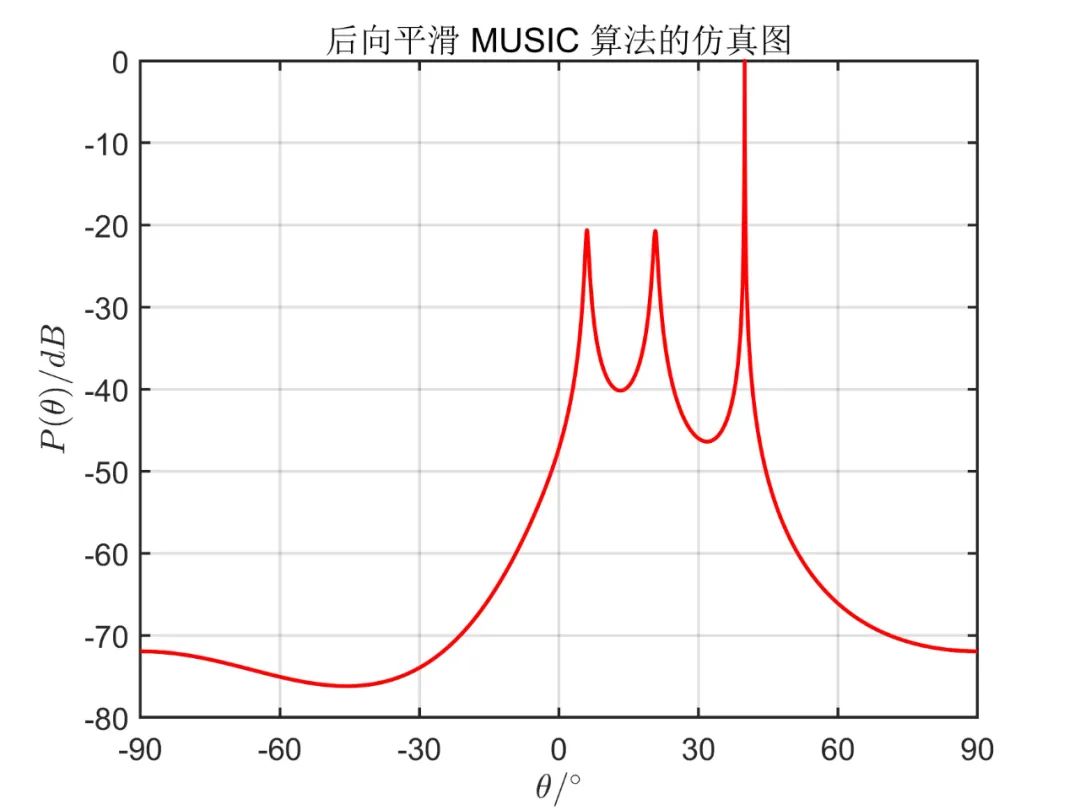
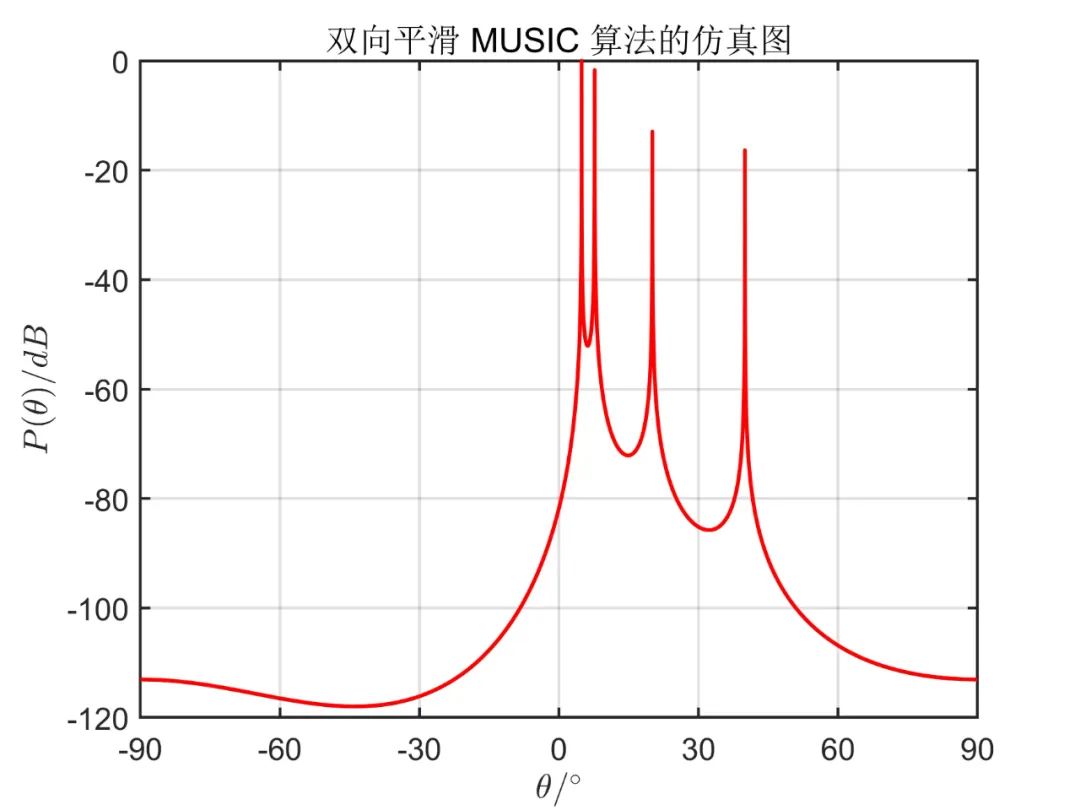
從仿真效果中可以看出,傳統(tǒng) MUSIC 算法無(wú)法正確估計(jì)相干信號(hào)源方向,而空間平滑算法能準(zhǔn)確估計(jì)出相干信號(hào)源方向,且從仿真效果可以看出,雙向平滑算法(MSS)分辨率要明顯好于前后向平滑算法(SS)。
本文理論部分參考自《空間譜估計(jì)理論與算法》。
在上期我們介紹了降維處理解相干可分為空間平滑和矩陣重構(gòu)兩類算法。
矩陣重構(gòu)類算法
下面討論矩陣重構(gòu)類算法,矩陣重構(gòu)類算法主要分為三類:一是矢量奇異值法;二是矩陣分解算法;三是 Toeplitz 類算法。
矢量奇異值法(SVD)
對(duì)數(shù)據(jù)協(xié)方差矩陣進(jìn)行分解可以分別得到由信號(hào)特征矢量組成的信號(hào)子空間及由噪聲特征矢量組成的噪聲子空間,且信號(hào)源完全不相關(guān)時(shí),信號(hào)子空間的維數(shù)等于信號(hào)源數(shù),而當(dāng)信號(hào)源相干時(shí),信號(hào)子空間的維數(shù)會(huì)減少。那么這個(gè)信號(hào)特征矢量與導(dǎo)向矢量之間有什么關(guān)系?
假設(shè) 個(gè)窄帶遠(yuǎn)場(chǎng)信號(hào)入射到 個(gè)陣元組成的陣列上,則陣列流型矩陣的秩為 ,信號(hào)協(xié)方差矩陣的秩為 ,假設(shè)噪聲協(xié)方差矩陣 為滿秩矩陣,則有如下線性關(guān)系滿足
其中, , 為特征矢量, 為線性組合因子。
由上述分析可知,當(dāng)噪聲協(xié)方差矩陣為理想白噪聲時(shí),上式可簡(jiǎn)化為
上式說(shuō)明無(wú)論信號(hào)源是否相干,對(duì)應(yīng)大特征值的特征矢量是各信號(hào)源導(dǎo)向矢量的一個(gè)線性組合。考慮最極端的情況,如 (信號(hào)源完全相干)時(shí),上式左邊只有一個(gè)最大特征值對(duì)應(yīng)的特征矢量
該式說(shuō)明數(shù)據(jù)協(xié)方差矩陣的最大特征矢量 包含所有信號(hào)的信息。我們會(huì)想到能否直接利用最大特征矢量來(lái)解相干?答案是肯定的。根據(jù)上式,可以重新構(gòu)造如下一個(gè)矩陣
式中, , , 。
上式組成的協(xié)方差矩陣可以表示為如下形式
其中, ,矩陣 , 分別為 個(gè)信號(hào)組成的維數(shù)為 和 的陣列流型。如果對(duì) 進(jìn)行奇異值分解有
其中, 是一個(gè) 的由奇異值組成的矩陣, 是左奇異矩陣, 是右奇異矩陣,則理想情況下矩陣 的非零奇異值為 個(gè),也就是小奇異值對(duì)應(yīng)的左奇異矩陣中的矢量組成的空間即是噪聲子空間,非零奇異值對(duì)應(yīng)的矢量即是信號(hào)子空間。
上述定理提供了一種有效的解相干算法——特征矢量奇異值法(ESVD)。另外需注意,將矩陣 中的最大特征矢量 換成無(wú)噪聲的快拍數(shù)據(jù)后,就是一種直接針對(duì)數(shù)據(jù)處理的矢量奇異值法(DSVD)。其數(shù)據(jù)矢量通過下式獲得
其中, 是 的一個(gè)參考陣元的數(shù)據(jù)矢量, 是 的陣列接收數(shù)據(jù)矩陣, 為快拍數(shù),也就是數(shù)據(jù)接收矩陣與參考陣元數(shù)據(jù)相乘的平均,然后用得到的數(shù)據(jù)矢量 代替矢量 重構(gòu)數(shù)據(jù)矩陣 。
由上述說(shuō)明可以看出,矢量奇異值算法的共同點(diǎn)在于找出一個(gè)矢量,這個(gè)矢量要包含所有的信號(hào)信息,這樣在重構(gòu)的數(shù)據(jù)陣中就可估計(jì)出相干信號(hào)源的信號(hào)或噪聲子空間。
基于矢量奇異值算法的 MUSIC 計(jì)算過程如下所示。
通過預(yù)處理得到一個(gè)數(shù)據(jù)矢量
利用數(shù)據(jù)矢量重構(gòu)矩陣
利用 MUSIC 算法進(jìn)行 DOA 估計(jì)
關(guān)于基于矢量奇異值算法的 MUSIC,作如下進(jìn)一步說(shuō)明:
矢量重構(gòu)算法與空間平滑算法相似,解相干的性能都是通過降低自由度獲得的
數(shù)據(jù)重構(gòu)矩陣 是一個(gè) 矩陣,其中 ,所以為了正確估計(jì)信號(hào),必須滿足 , 。另外,由于矩陣 是一個(gè)長(zhǎng)方陣,所以在利用 MUSIC 算法進(jìn)行 DOA 估計(jì)時(shí),需用奇異值分解,而不是特征值分解
這類算法一般只適用于均勻線陣
下面為在 信噪比條件下, 個(gè)相干信號(hào)源分別從 入射時(shí)傳統(tǒng) MUSIC 算法的成像效果以及 SVD 的 MUSIC 成像效果。其中,陣列天線數(shù) 。
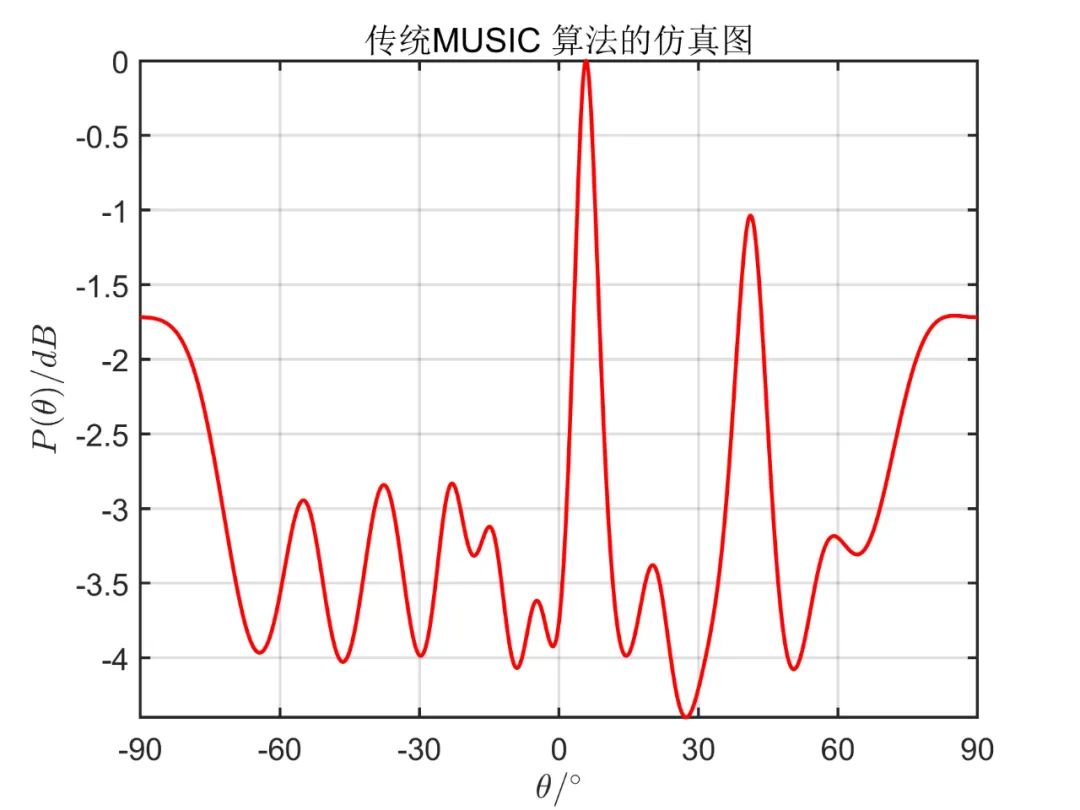
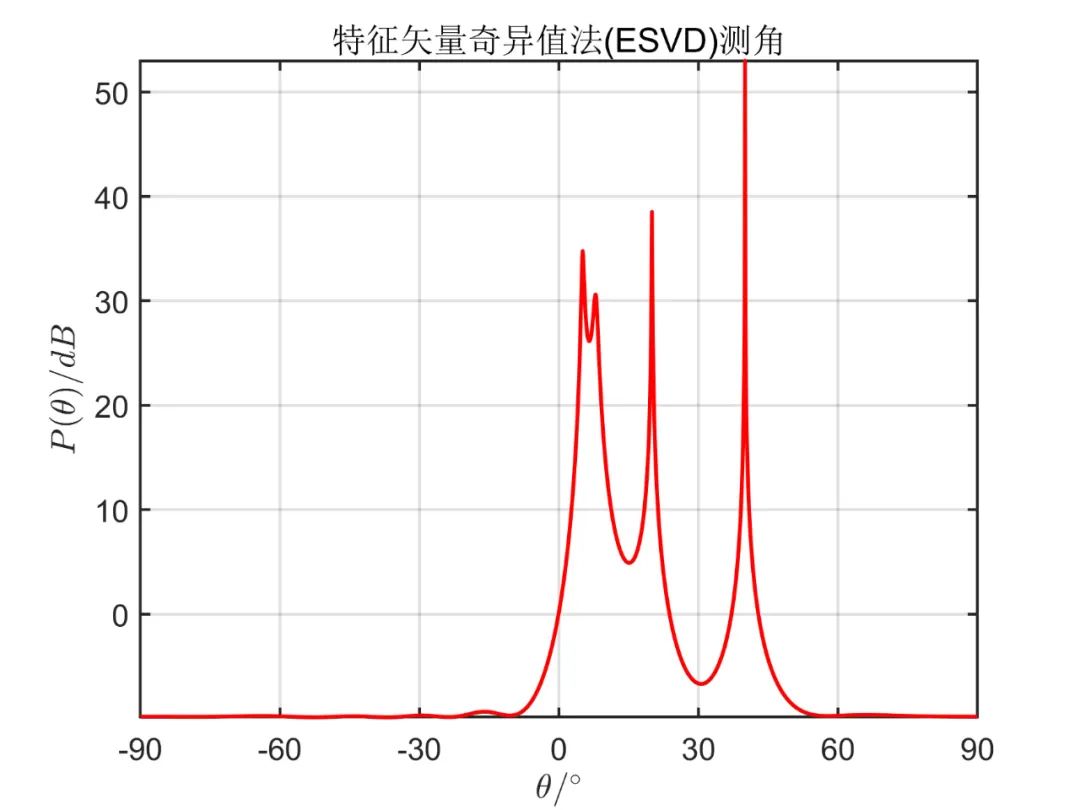
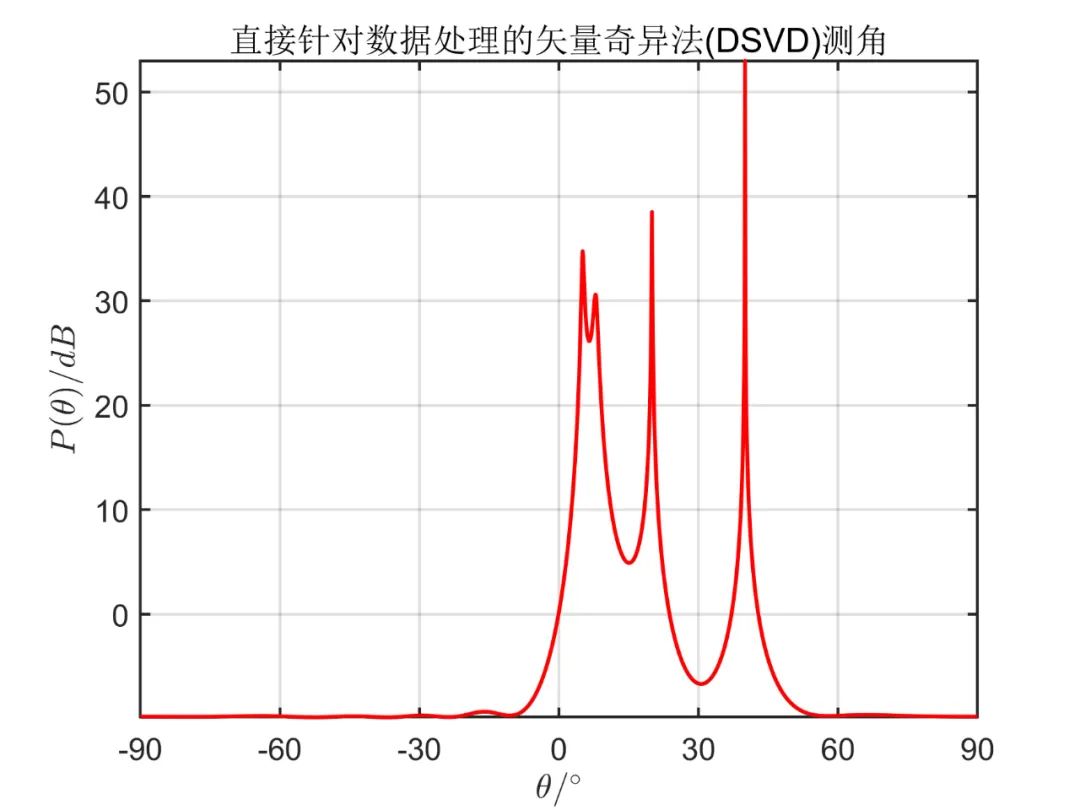
從仿真效果中可以看出,傳統(tǒng) MUSIC 算法無(wú)法正確估計(jì)相干信號(hào)源方向,而 SVD 算法能準(zhǔn)確估計(jì)出相干信號(hào)源方向。
矩陣分解算法
矩陣分解算法也是一類矩陣重構(gòu)的算法,但它的重構(gòu)與上述的奇異矢量法不同。
設(shè) 是 維無(wú)零行矢量的矩陣( ), 是 維對(duì)角陣,其對(duì)角元素互不相等,若 ,則 ,也就是新的矩陣 的秩為 。
若 ,則有
其中, , 為信號(hào)源數(shù), 為陣列接收數(shù)據(jù)協(xié)方差陣, 矩陣 為 的第 行到 行構(gòu)成的矩陣。
顯然上式所示的 MD 算法是針對(duì)理想情況下的矩陣重構(gòu),與空間平滑技術(shù)相似,為了提高解相干的性能,可以在修正矩陣中添加反向平滑項(xiàng),即得 MMD 算法的修正矩陣
這樣做的好處與雙向平滑的空間平滑技術(shù)相同,可以再提高陣列解相干信號(hào)的能力,即解相干源的能力與 MSS 算法相同。
另外,我們也提出了一種減小計(jì)算量的修正的矩陣分解算法,其思想是將空間平滑技術(shù)應(yīng)用到矩陣分解中,稱之為 SMD 算法。從前面空間平滑的技術(shù)中可知,前向平滑后的修正矩陣為 ,后向平滑矩陣為 ,則得到 SMD 算法的修正矩陣為
對(duì)上面修正矩陣的處理有一個(gè)明顯的好處:對(duì)修正矩陣的奇異值分解計(jì)算量明顯少于對(duì) MMD 算法的修正矩陣的奇異值分解,并且算法的穩(wěn)定性也有相當(dāng)大的提高。
根據(jù)以上的理論分析,將基于矩陣分解的解相干算法歸納為下面所述的步驟。
對(duì)陣列的數(shù)據(jù)協(xié)方差矩陣進(jìn)行重構(gòu)
對(duì)重構(gòu)的矩陣進(jìn)行奇異值分解,得到數(shù)據(jù)的信號(hào)子空間與噪聲子空間
利用 MUSIC 算法進(jìn)行 DOA 估計(jì)
對(duì)于基于矩陣分解的解相干算法,還應(yīng)注意以下幾點(diǎn):
矩陣分解算法、矢量重構(gòu)算法與空間平滑算法相似,解相干的性能都是通過降低自由度獲得的
數(shù)據(jù)重構(gòu)矩陣 是一個(gè) 矩陣,為了正確估計(jì)相干信號(hào)源,必須滿足 且 大于相干源的數(shù)目
當(dāng)相干源數(shù)多時(shí),SVD 算法的運(yùn)算量要小很多
相同條件下 MMD 算法的仿真如下所示。
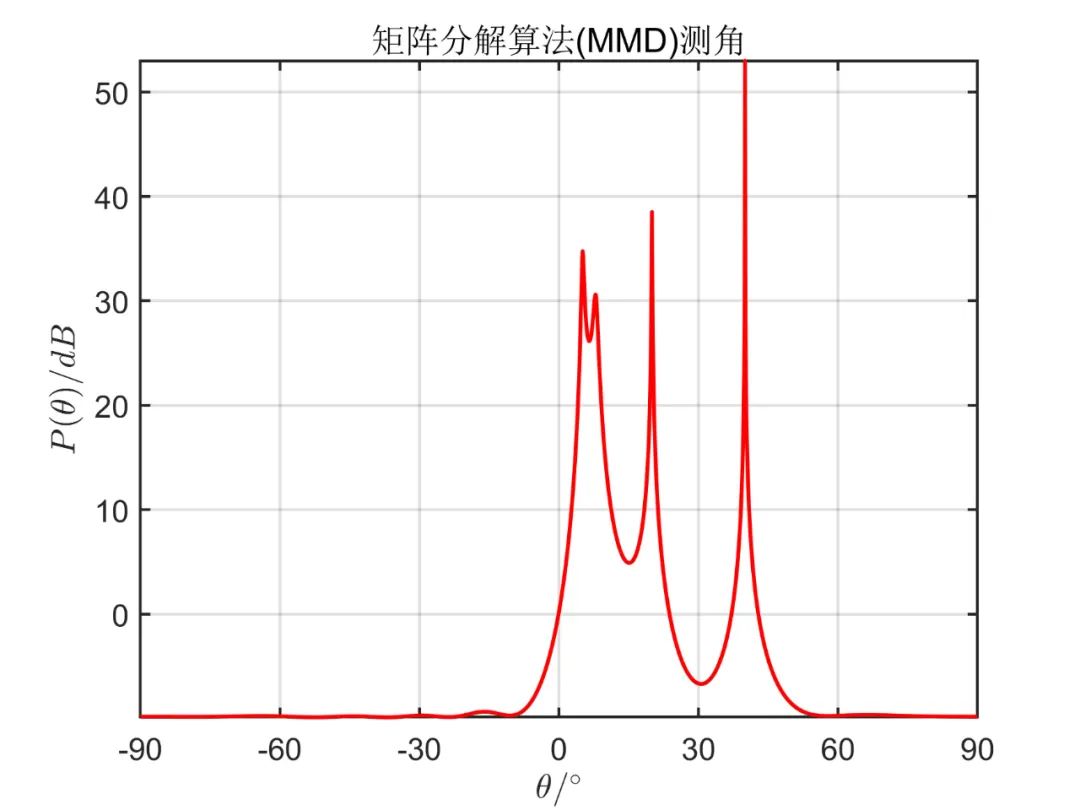
前面討論的 MUSIC 及相關(guān)應(yīng)用場(chǎng)合的算法都是建立在陣元空間基礎(chǔ)上的,即每個(gè)陣元都對(duì)應(yīng)于一個(gè)數(shù)據(jù)處理的通道。這一節(jié)討論波束空間的 MUSIC 處理。所謂的波束空間是指先將空間陣元通過變換合成一個(gè)或幾個(gè)波束,再利用合成的波束數(shù)據(jù)進(jìn)行 DOA 估計(jì),其原理如下圖所示。
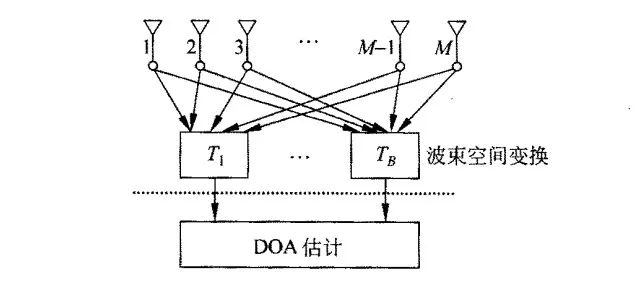
從圖中可知,波束空間處理需要通過陣元合成一定數(shù)量波束通道作為數(shù)據(jù)接收通道,這和陣元空間處理中每個(gè)陣元對(duì)應(yīng)于一個(gè)接收通道完全不同。
我們知道,基于特征分解的信號(hào)子空間算法的運(yùn)算量為 ,所以對(duì)于大陣列、小信號(hào)源數(shù)的場(chǎng)合,這類算法很難實(shí)時(shí)實(shí)現(xiàn)。
顯然,波束空間方法在這種場(chǎng)合下能有效降低算法的計(jì)算量,如果合成波束的維數(shù) ,則 DOA 估計(jì)的計(jì)算量由 降為 ,所以在合成的波束數(shù) 遠(yuǎn)小于陣元數(shù) 時(shí)算法的運(yùn)算量顯著下降。
同樣,就系統(tǒng)設(shè)計(jì)而言,數(shù)據(jù)接收通道的減少可以大大減少系統(tǒng)的復(fù)雜性。
波束形成原理及算法
通過前面的知識(shí)可知,對(duì)于 陣元間距為 的均勻線陣,陣列的導(dǎo)向矢量
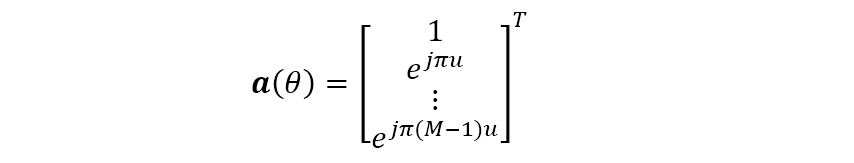
顯然,上式可以表示成 函數(shù),即 就對(duì)應(yīng)線陣的觀察范圍為 。注意到由 點(diǎn)離散傅里葉變換因子組成的矢量
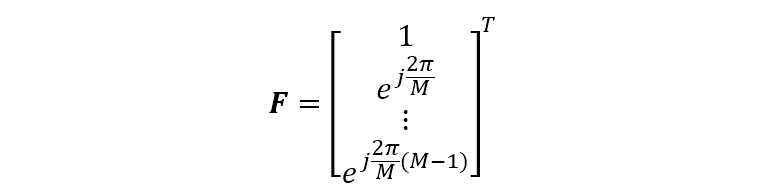
該式表明式陣列的導(dǎo)向矢量也是離散傅里葉變換的一種形式,只是傅里葉變換的因子中 變?yōu)?,則有第 次快拍數(shù)據(jù)的離散傅里葉變換
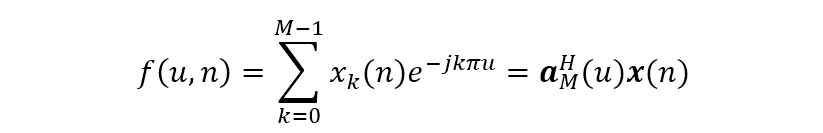
上式表明陣列的導(dǎo)向矢量其實(shí)是一個(gè)波束形成器,其權(quán)值即是 ,形成的波束主瓣指向 。因?yàn)?,即 的周期為 可定義如下一個(gè) 的波束形成矩陣
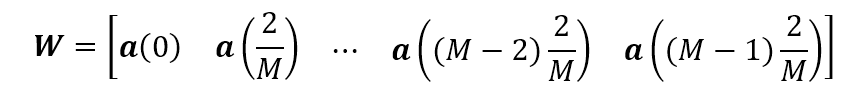
由上面的分析可知,式中每一列表示波束主瓣指向 的波束形成器,其中 ,則上式共有 個(gè)波束形成器,各相鄰主瓣指向的間隔為 。
回到我們的主題,我們的目的是通過陣列的接收數(shù)據(jù)形成 個(gè)波束,如何才能形成這 個(gè)波束?很顯然可以通過選擇上式中相鄰的 個(gè)波束形成器來(lái)形成所需要的歸一化加權(quán)矩陣(該方法記為 )
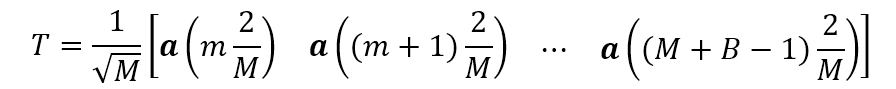
該式就是基于 DFT 波束形成的方法,采用上式的好處在于形成的變換矩陣滿足
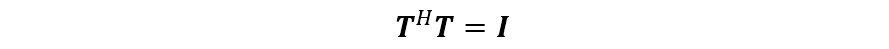
則通過波束空間變換后的輸出
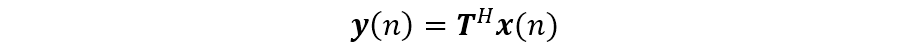
當(dāng) 時(shí),上式仍為陣元空間的處理,可用常規(guī)的 MUSIC 算法。另外,由上式還可知波束輸出由 矢量變?yōu)?矢量,對(duì)應(yīng)的協(xié)方差矩陣為
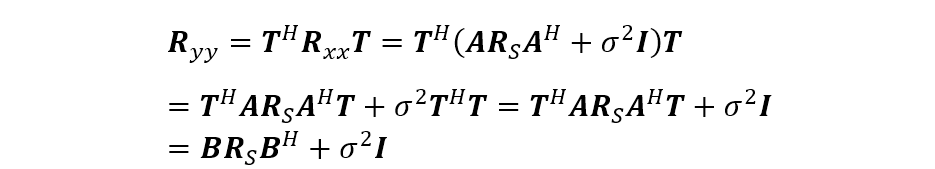
其中, 。對(duì)上式進(jìn)行特征分解得到噪聲子空間 ,再應(yīng)用 MUSIC 算法即得波束空間的 MUSIC 算法
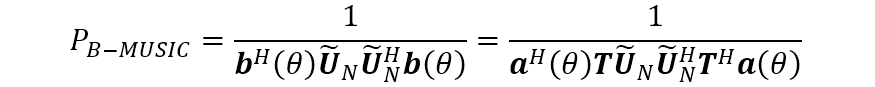
除了上面給出的 的一種取值方法外,還有其他取值方法,它們的目的都是通過 個(gè)陣列的接收數(shù)據(jù)形成 個(gè)波束,然后通過波束空間的處理方法得到信號(hào)源的方位信息。下面討論一些其他的 取值方法。
(1)設(shè) 是一個(gè) 的列矢量(該方法記為 ),令
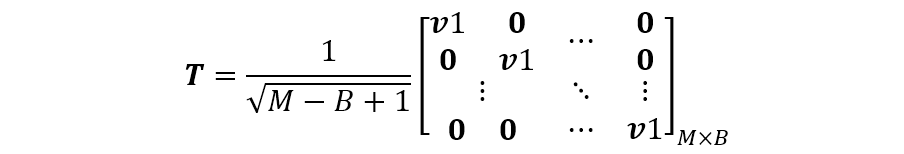
顯然,上式不滿足 ,即變換矩陣為非正交變換(可以通過處理使之正交化)。
分析上式,不難發(fā)現(xiàn)通過波束空間變換后的輸出與前節(jié)分析的空間平滑的思想相似,即相當(dāng)于對(duì)一個(gè) 陣元的陣列進(jìn)行 的平滑,而子陣的陣元數(shù)為 ,即每個(gè)子陣的輸出為子陣各陣元的求和。
(2)設(shè) 是正整數(shù), 是一個(gè) 的列矢量(該方法記為 ),則 取如下的矩陣
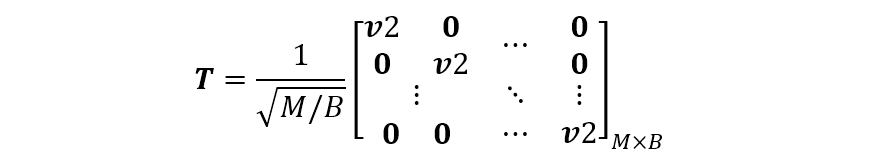
式中的 指的是由 組成的矢量。通過變換后的陣列輸出相當(dāng)于將整個(gè)陣列分為 個(gè)子陣,每個(gè)子陣的陣元數(shù)為 ,而每個(gè)子陣的輸出為子陣各陣元的求和,且該式滿足 ,即上式也是一個(gè)正交變換,這種變換方式一般適合大陣列。
(3)定義一個(gè) 矩陣 ,可以取波束形成矩陣 如下
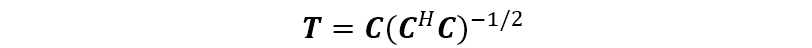
當(dāng)考察兩個(gè)相鄰信號(hào)的分辨力問題時(shí),可以取 如下(該方法記為 )
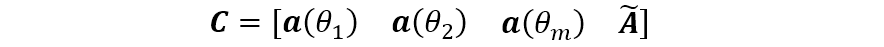
其中, , 是一個(gè) 的滿秩矩陣。或者對(duì)于某一確定的觀察區(qū)域 ,將之平分為 份,間隔 ,則可以取矩陣 如下(該方法記為 )
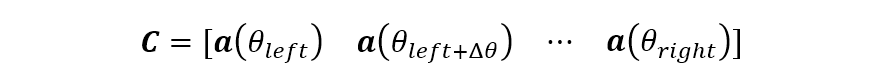
另外 的另一種取法為(該方法記為 )
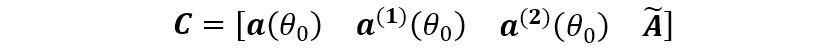
式中, , 分別為導(dǎo)向矢量 的一階導(dǎo)數(shù)和二階導(dǎo)數(shù),式中取 。
注意:需要將矩陣 代入 中得到波束形成矩陣 。
(4)定義如下一個(gè)矩陣
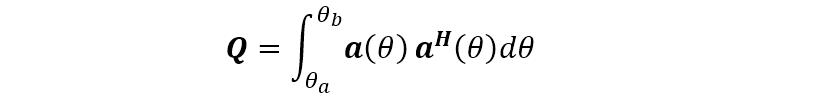
則波束形成矩陣可以取矩陣 的 個(gè)大特征值對(duì)應(yīng)的特征矢量(該方法記為 ),即
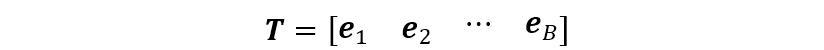
上式也是一種波束形成器。已有文獻(xiàn)證明,對(duì)于均勻線陣,該波束形成器是最優(yōu)的。當(dāng)然當(dāng) 小于 個(gè)波束寬度時(shí),可以定義如下的矩陣
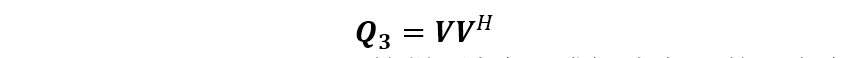
式中, 。這樣,波束形成矩陣由 的三個(gè)大特征值對(duì)應(yīng)的特征矢量及剩余的其他特征矢量中的 個(gè)特征矢量組成(該方法記為 ),即
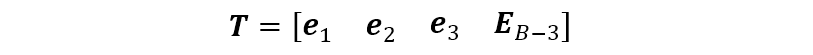
我們將波束空間 MUSIC 算法的計(jì)算過程總結(jié)于下:
由陣列的接收數(shù)據(jù)得到數(shù)據(jù)協(xié)方差矩陣
選擇不同的波束形成矩陣 ,利用 得到波束空間的數(shù)據(jù)矩陣
利用波束空間的數(shù)據(jù)矩陣進(jìn)行 MUSIC 譜估計(jì),找出極大值對(duì)應(yīng)的信號(hào)方向
對(duì)于波束空間的 MUSIC 算法,需要進(jìn)一步說(shuō)明的是:
波束空間的 MUSIC 算法實(shí)質(zhì)就是先將陣列形成幾個(gè)波束,換言之,就是將陣列接收的數(shù)據(jù)(陣元空間數(shù)據(jù))變換到波束空間的數(shù)據(jù),再利用波束空間的數(shù)據(jù)進(jìn)行 DOA 估計(jì)
波束空間的 MUSIC 算法在利用 MUSIC 算法進(jìn)行搜索時(shí),注意導(dǎo)向矢量的維數(shù)必須等于形成的波束數(shù),而且在對(duì)波束空間數(shù)據(jù)進(jìn)行特征分解時(shí),矩陣的維數(shù)也由原來(lái)的陣元數(shù)降為波束數(shù)
波束空間形成矩陣 的選擇決定波束空間算法的性能,但 的選擇不是任意的,只有各相鄰波束滿足一定的條件才能正確估計(jì)信號(hào)源的數(shù)目與方向
相關(guān)仿真分析
陣元數(shù)目為 ,形成的波束數(shù)目為 ,信源為 個(gè)相互獨(dú)立的信號(hào)源,其方位角分別為 , , , 。對(duì)應(yīng)的信噪比為 ,形成波束的初始陣元為 (第一個(gè)陣元),快拍數(shù)為 。圖如下所示。
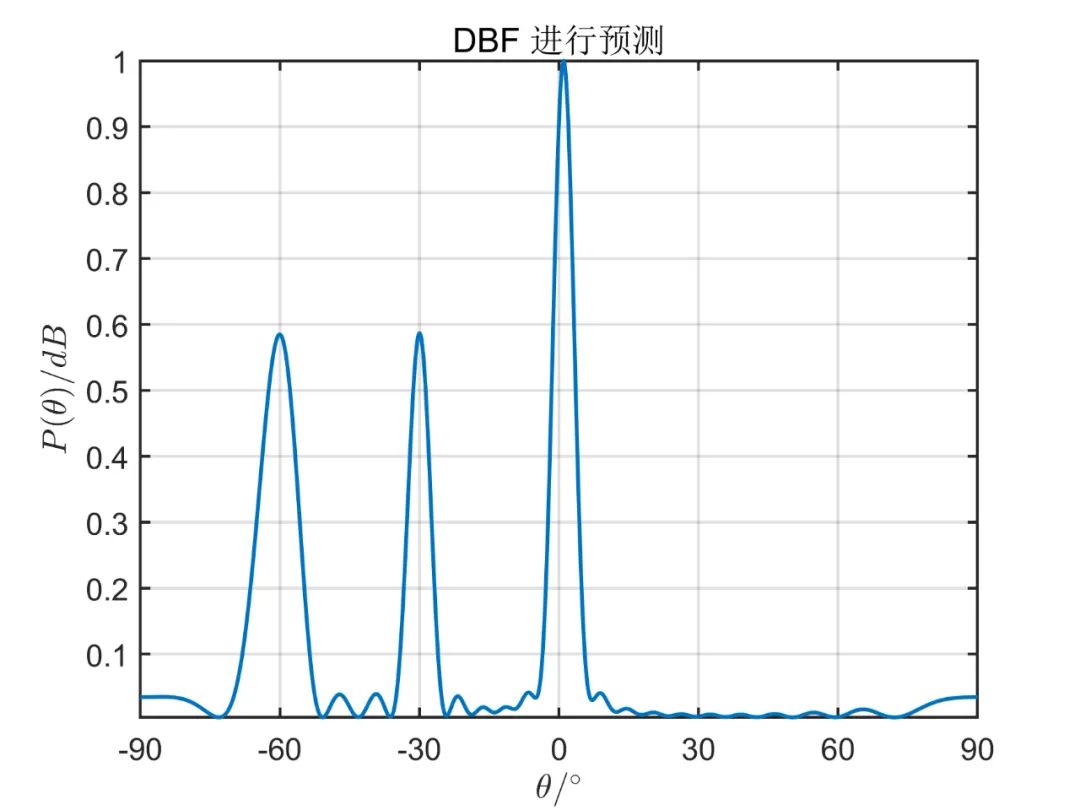
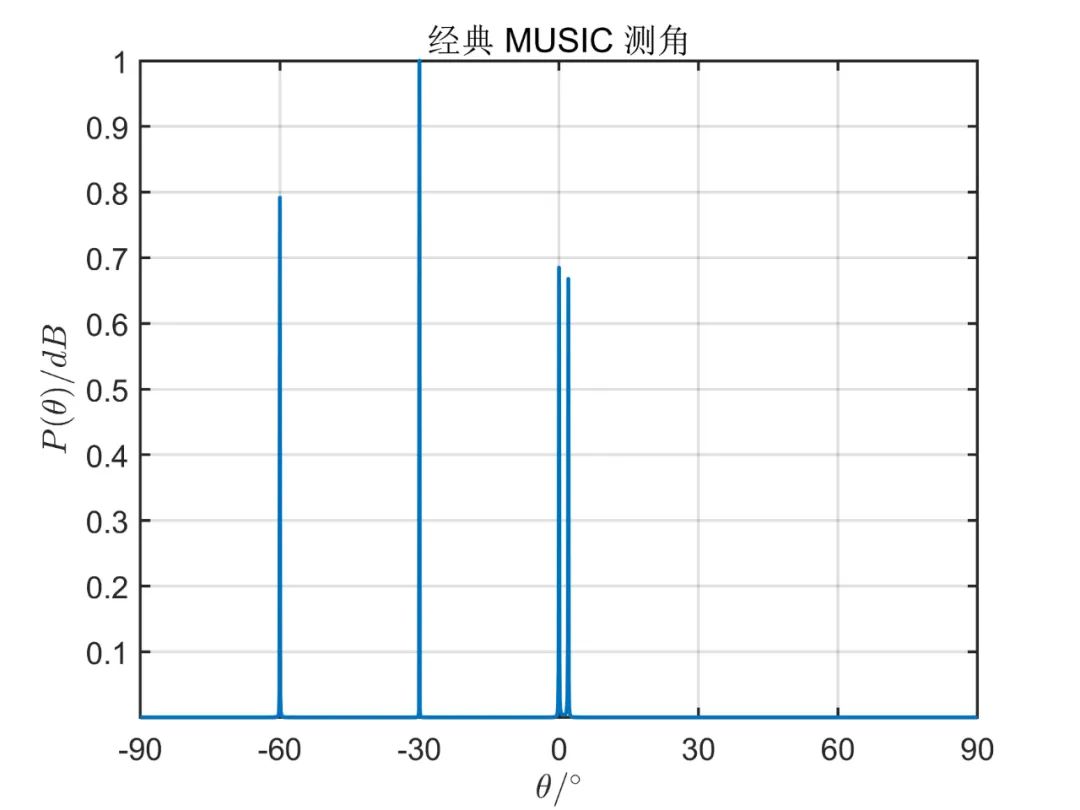
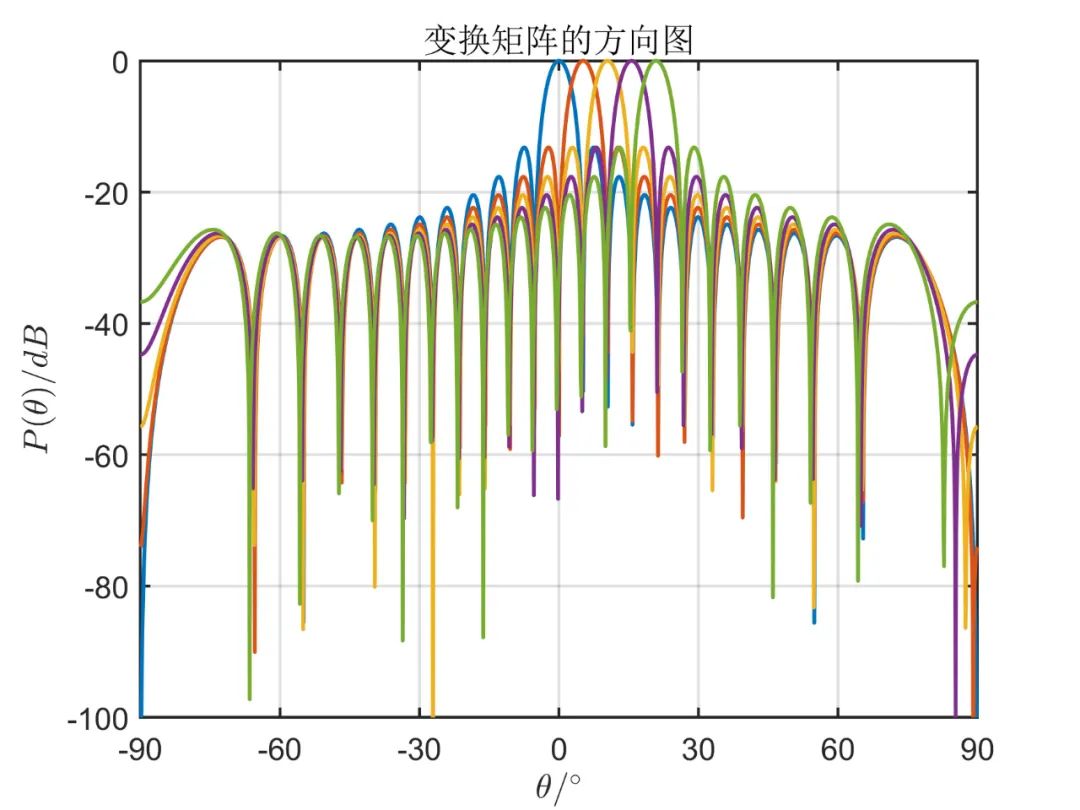
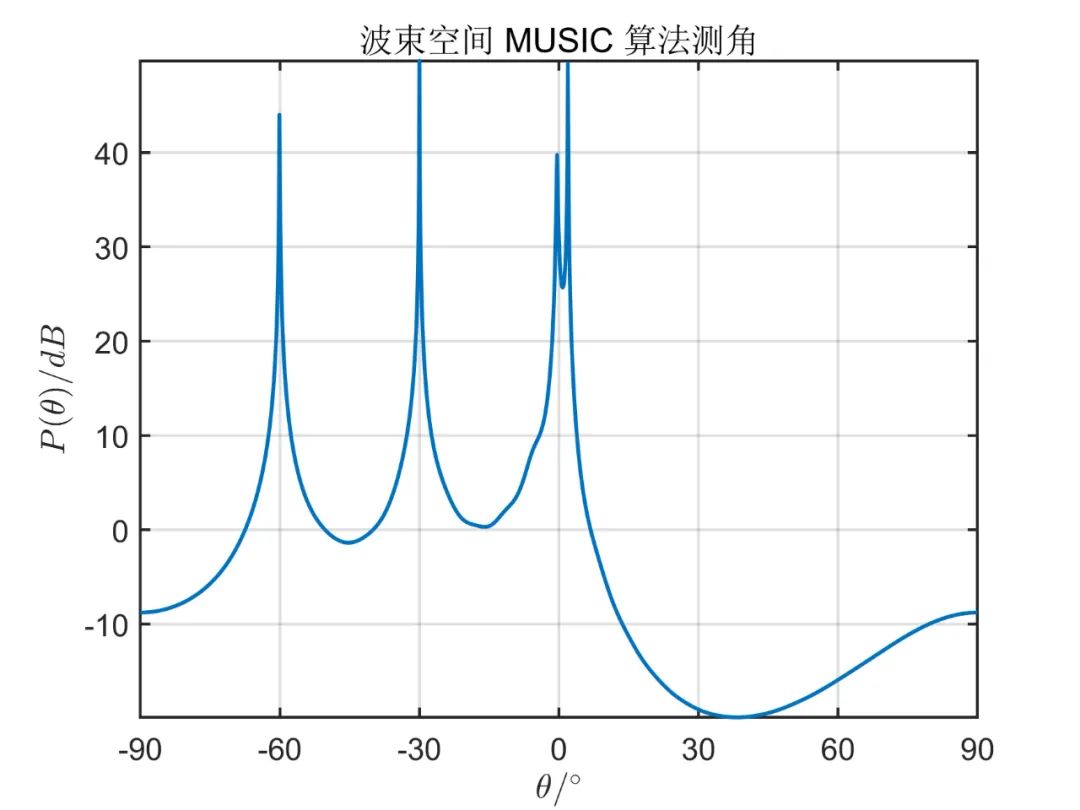
對(duì)于相關(guān)信號(hào),則只需要把相應(yīng)的調(diào)頻率寫為 即可,仿真結(jié)果如下圖所示。
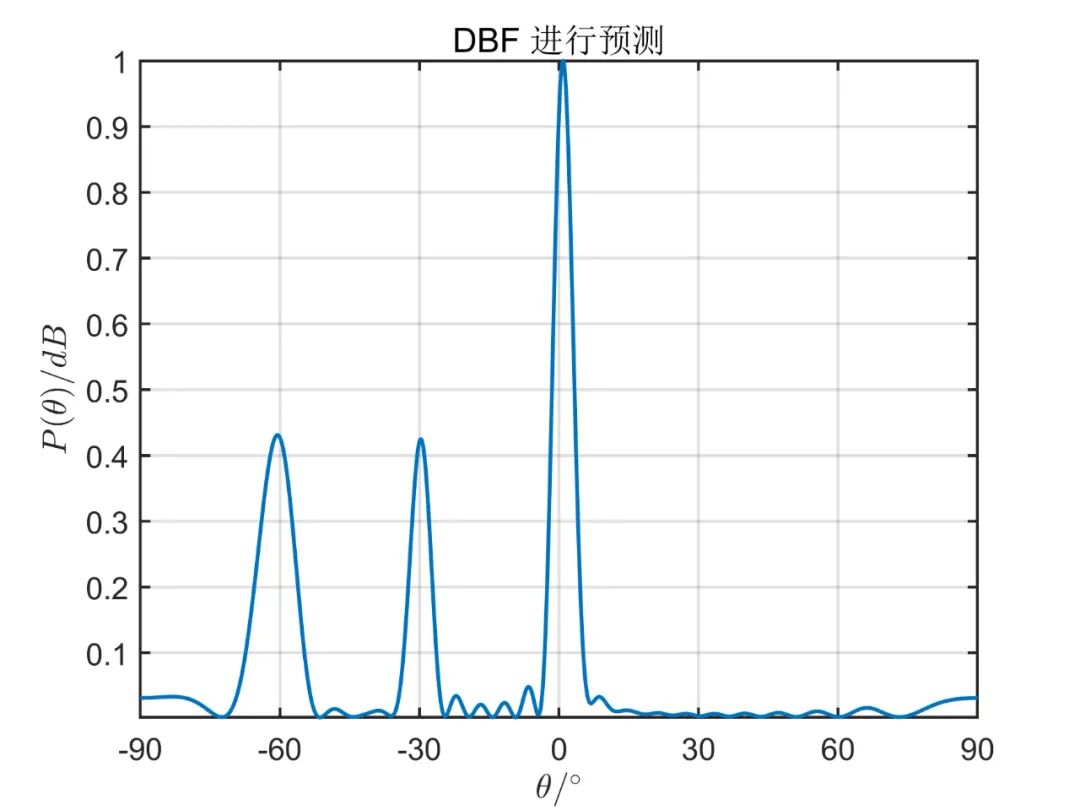
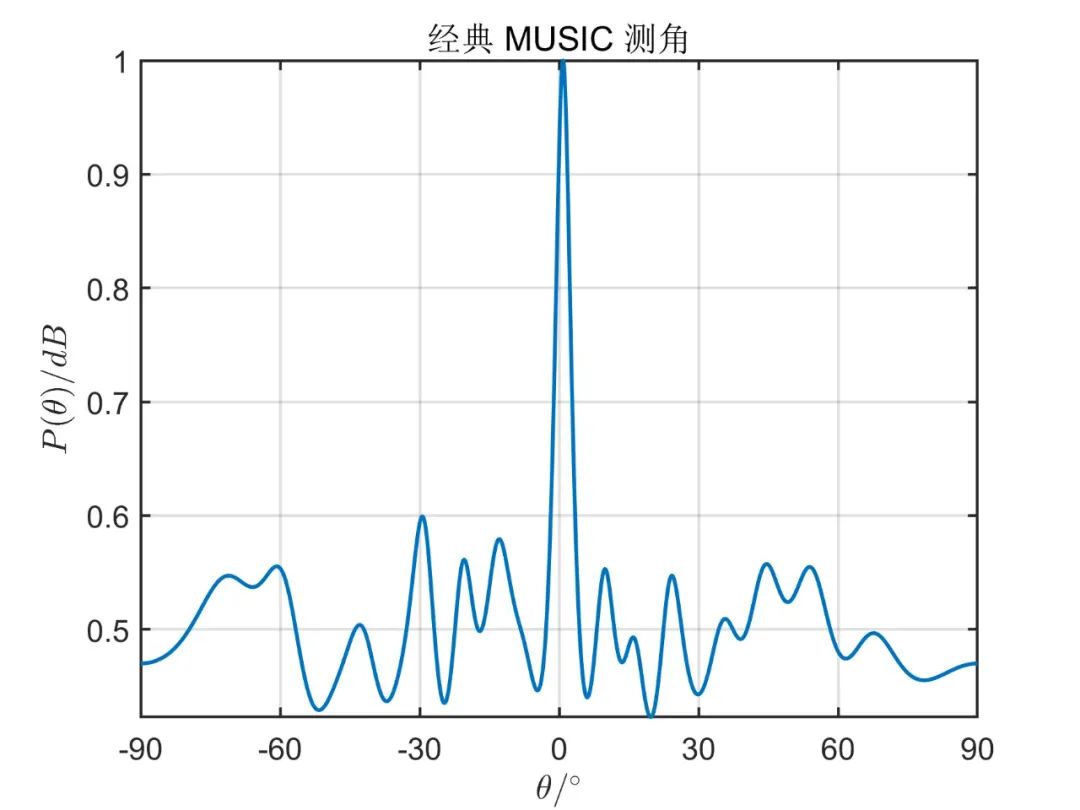

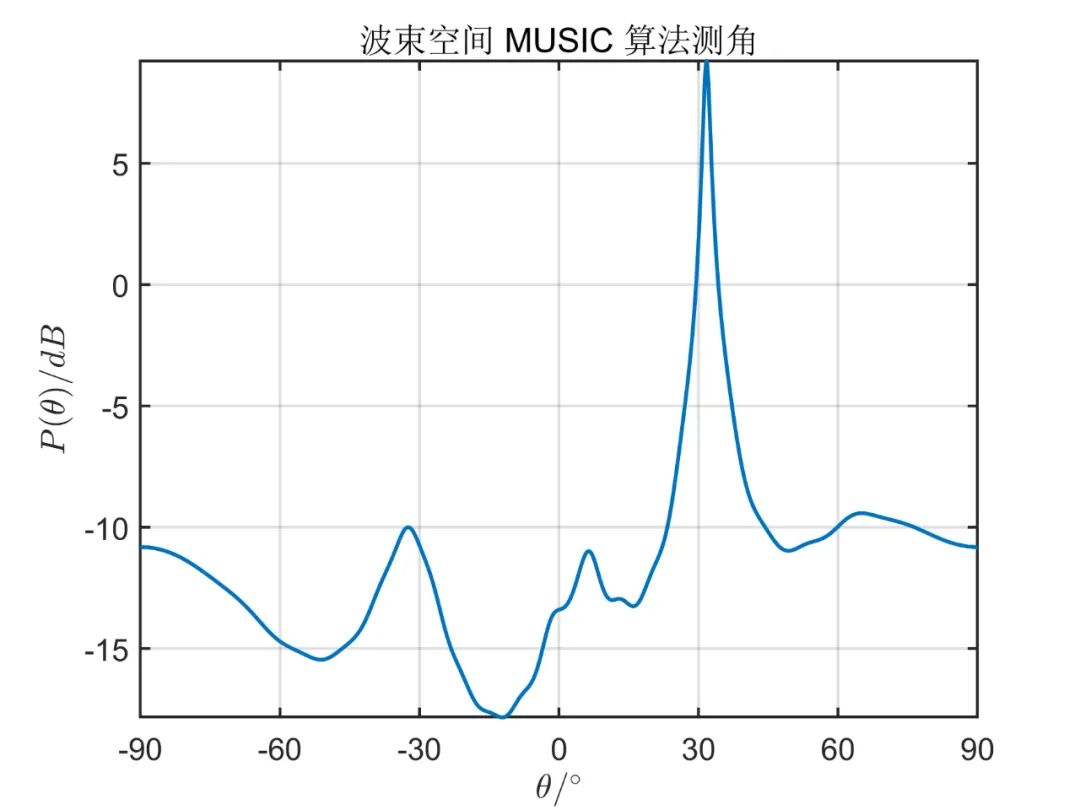
從上面的仿真對(duì)比,我們可以得出,一般情況下陣元空間的算法性能優(yōu)于波束空間,但是使用波束空間算法降低了系統(tǒng)的復(fù)雜性,降低了運(yùn)算量。 由于這種算法因其本質(zhì)上仍然是 MUSIC 算法,因此對(duì)于相干信號(hào),此算法也無(wú)法進(jìn)行解相干。
陣元數(shù)目為 ,信源為 個(gè)相互獨(dú)立的信號(hào)源,其方位角分別為 , 。對(duì)應(yīng)的信噪比為 ,形成波束的初始陣元為 (第一個(gè)陣元),快拍數(shù)為 ,形成的波束數(shù)目變化時(shí)測(cè)角性能和波束數(shù)目關(guān)系如下所示。
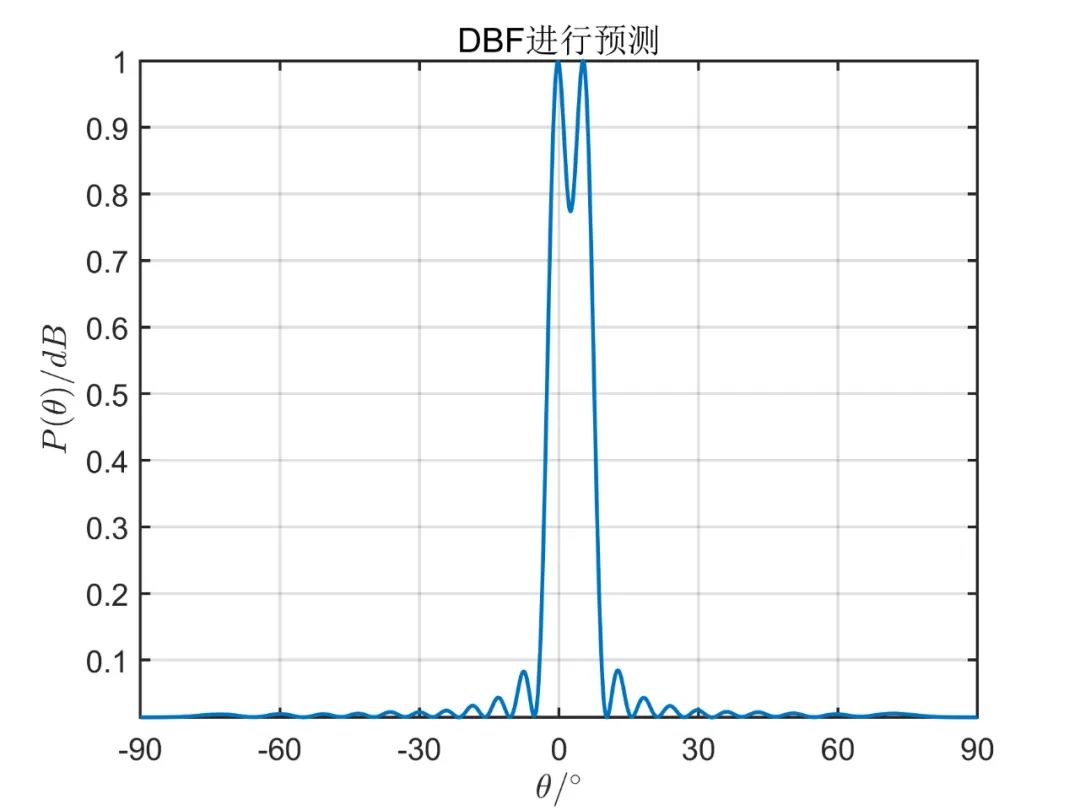
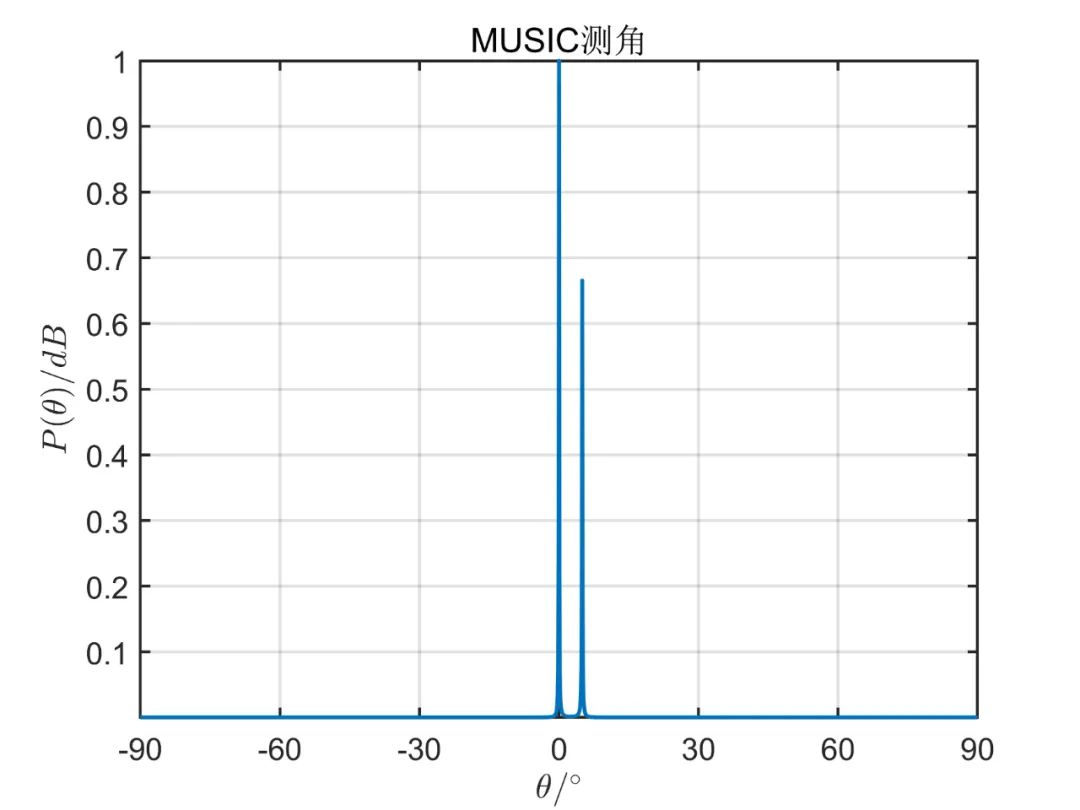
個(gè)波束空間時(shí)的測(cè)角性能:
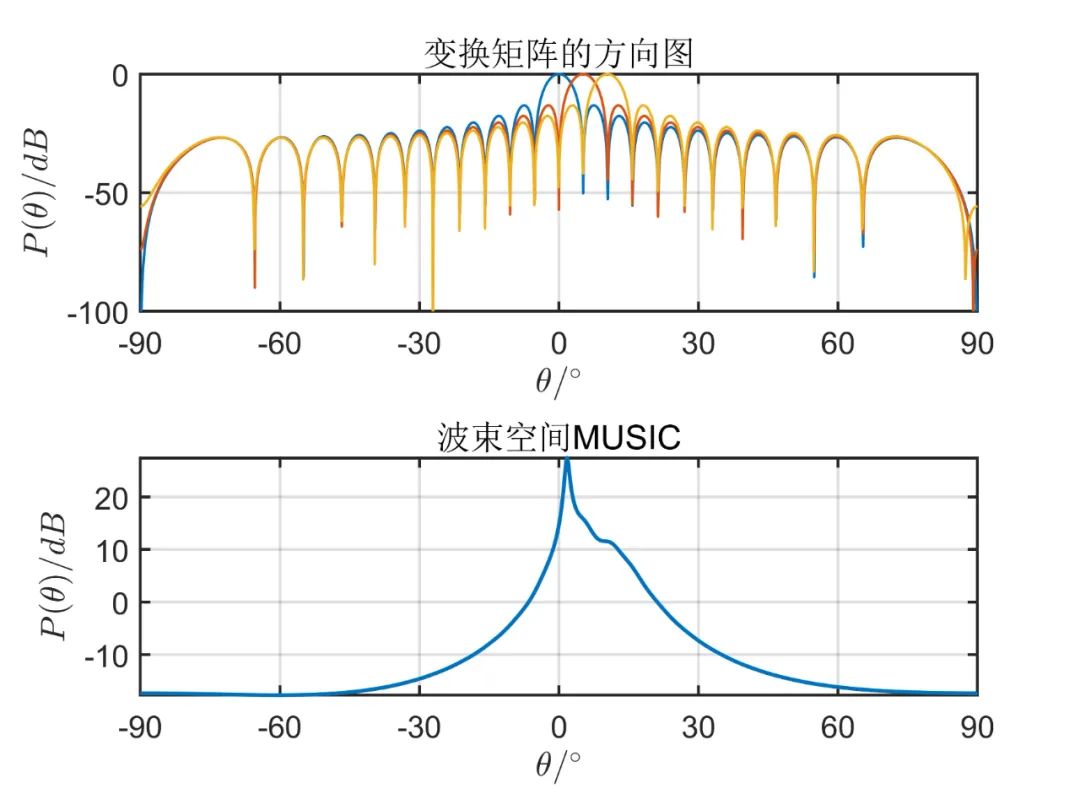
個(gè)波束空間時(shí)的測(cè)角性能:
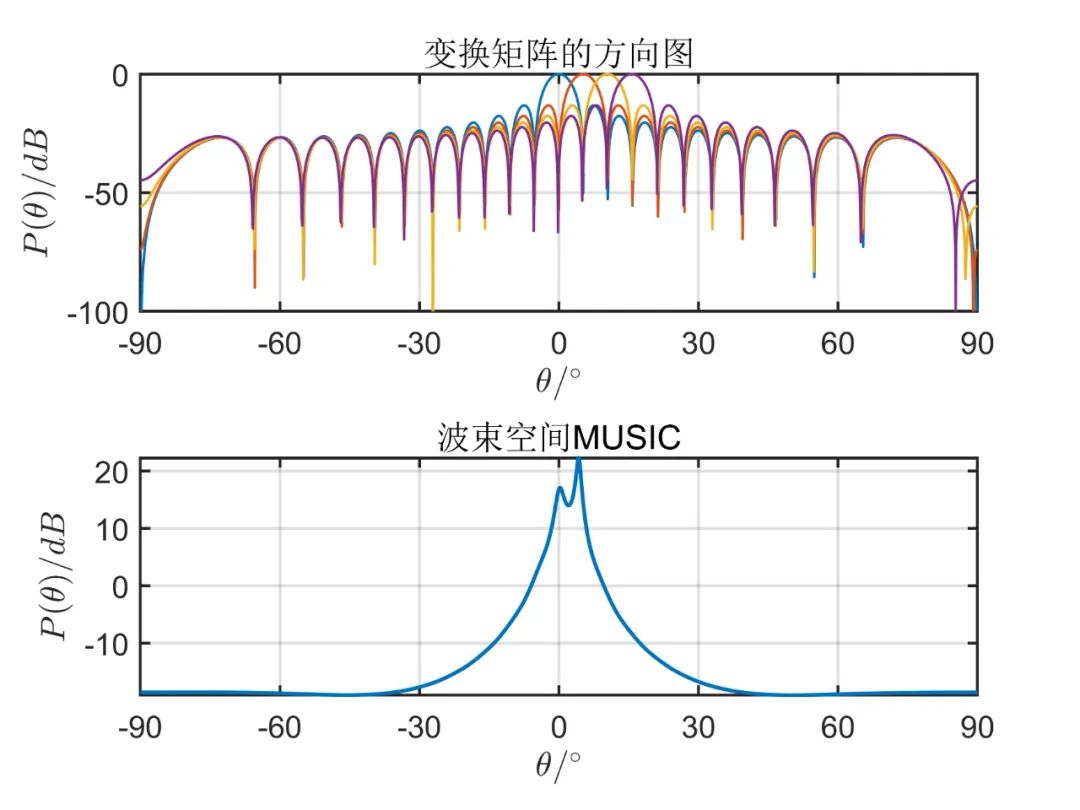
個(gè)波束空間時(shí)的測(cè)角性能:
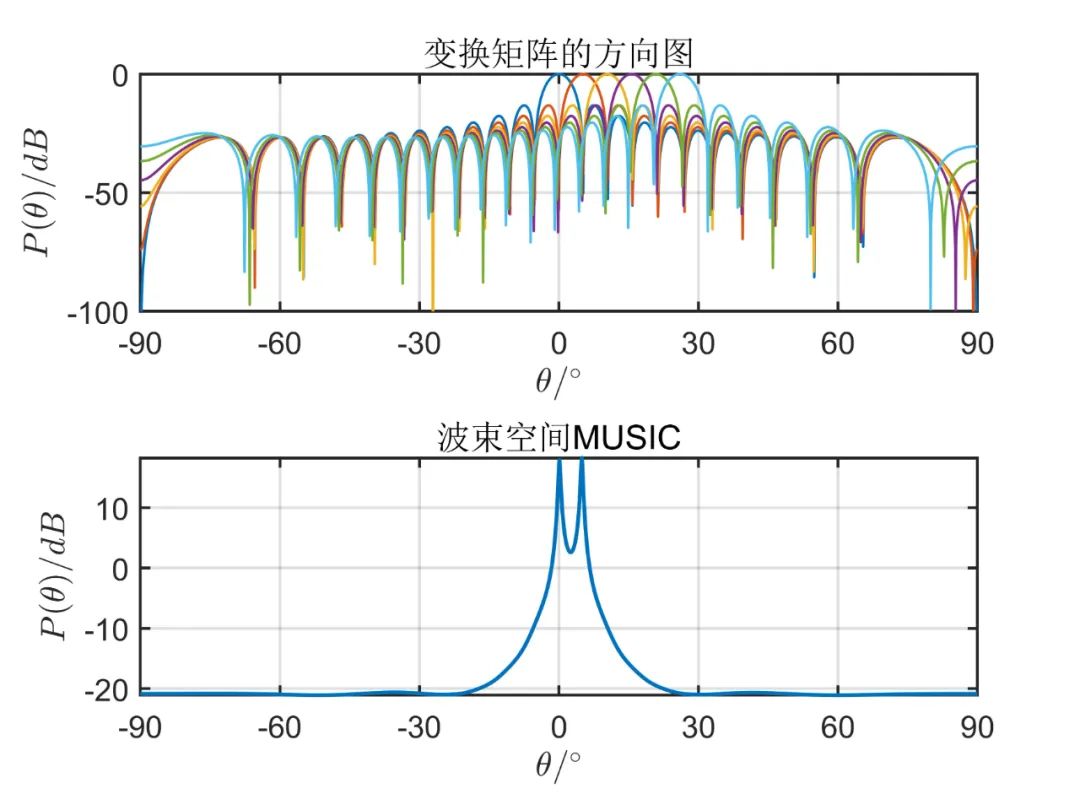
個(gè)波束空間時(shí)的測(cè)角性能:
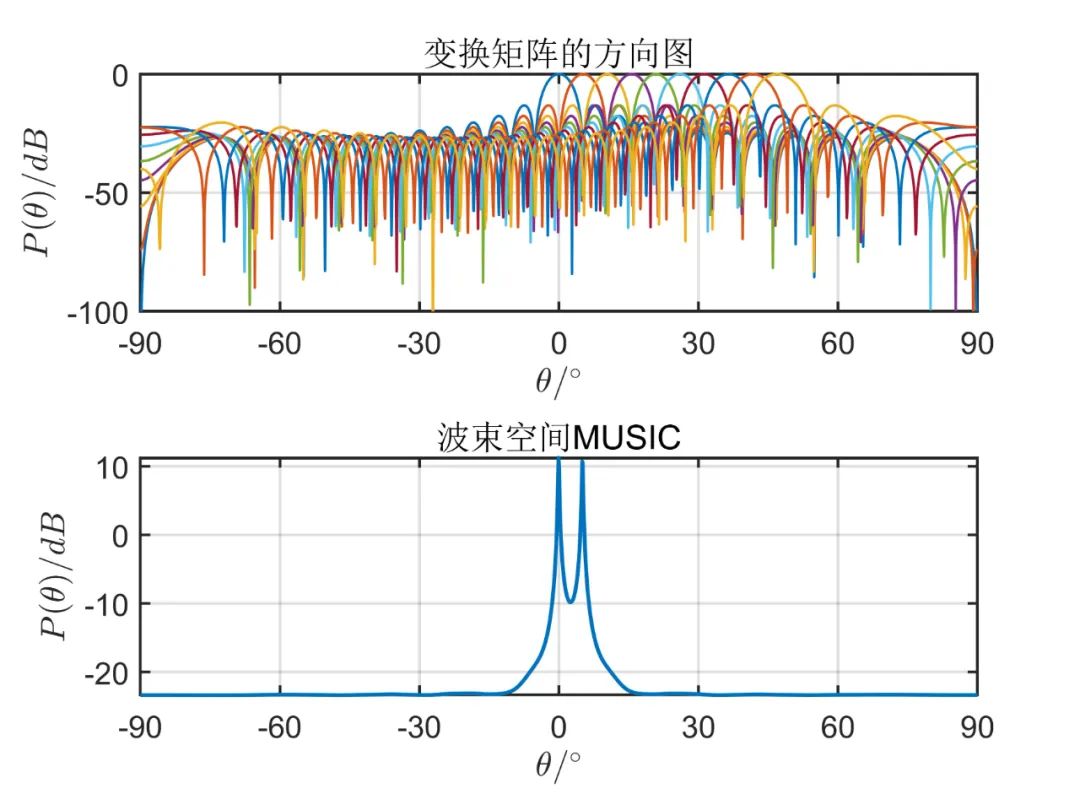
個(gè)波束空間時(shí)的測(cè)角性能:
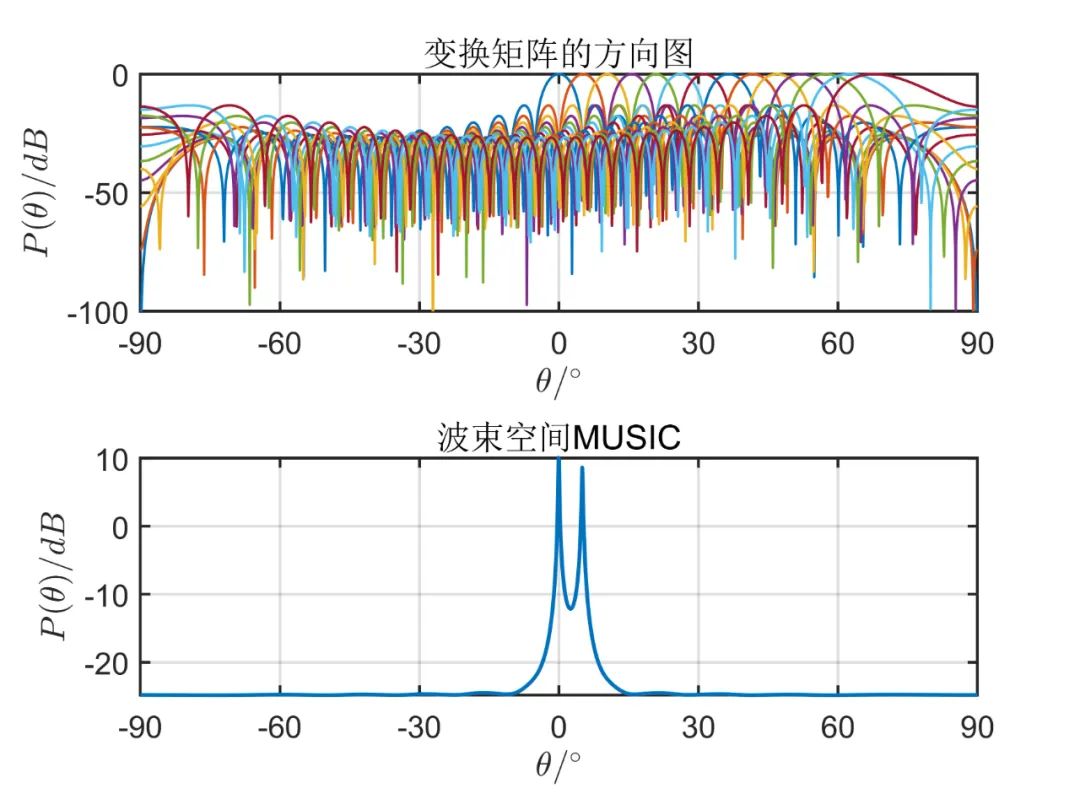
個(gè)波束空間時(shí)的測(cè)角性能:
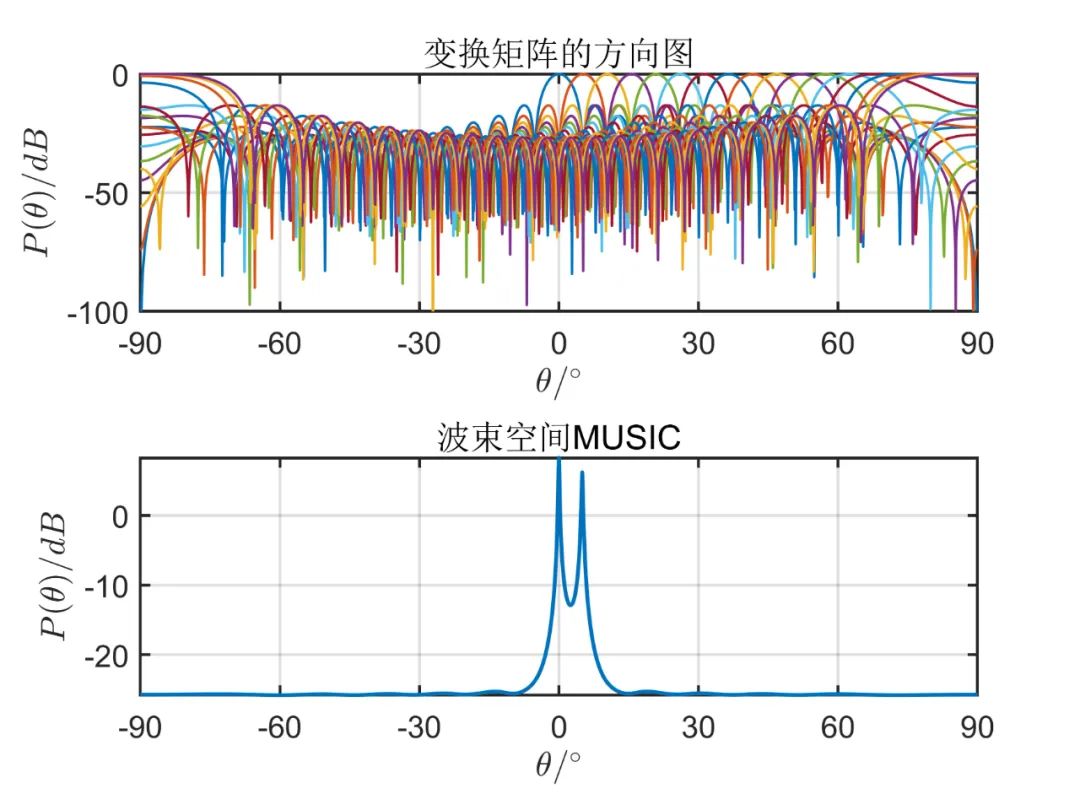
個(gè)波束空間時(shí)的測(cè)角性能:
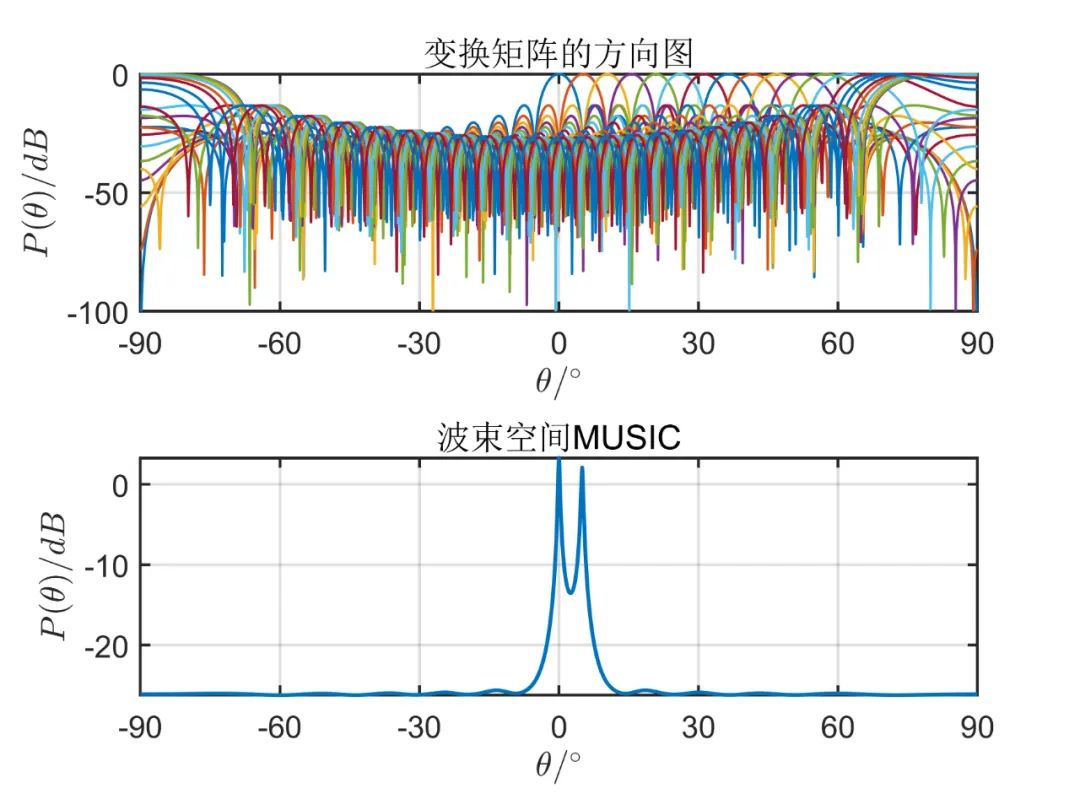
從上述仿真可以看出, 由仿真結(jié)果可見,波束空間的數(shù)目加大時(shí)會(huì)有效的改善空間角分辨能力,當(dāng)波束空間的數(shù)目等于陣元數(shù)目時(shí),這種算法的性能和常規(guī) MUSIC 算法是一樣的;但是波束空間數(shù)目增加時(shí)又會(huì)使計(jì)算負(fù)擔(dān)加大,那么這種算法的優(yōu)點(diǎn)也會(huì)消失。
原文標(biāo)題:相干信號(hào)源數(shù)學(xué)模型
文章出處:【微信公眾號(hào):云腦智庫(kù)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
審核編輯:湯梓紅
-
信號(hào)源
+關(guān)注
關(guān)注
5文章
495瀏覽量
45574 -
算法
+關(guān)注
關(guān)注
23文章
4702瀏覽量
94941 -
數(shù)學(xué)模型
+關(guān)注
關(guān)注
0文章
83瀏覽量
12218
原文標(biāo)題:相干信號(hào)源數(shù)學(xué)模型
文章出處:【微信號(hào):CloudBrain-TT,微信公眾號(hào):云腦智庫(kù)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
信號(hào)源結(jié)構(gòu)原理
矢量信號(hào)源與射頻信號(hào)源的區(qū)別?
激勵(lì)信號(hào)源軟件控制發(fā)生方法研究
關(guān)于時(shí)鐘信號(hào)源設(shè)計(jì)資料下載
射頻模擬信號(hào)源和矢量信號(hào)源的區(qū)別
功率信號(hào)源的使用方法有哪些
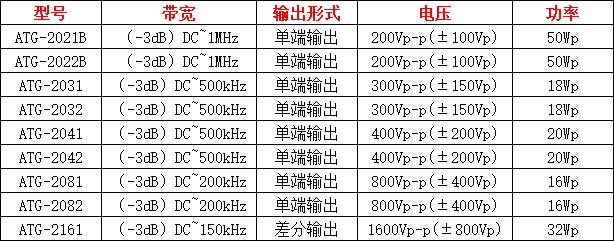
信號(hào)源矢量調(diào)制信號(hào)質(zhì)量的校準(zhǔn)方法有哪些
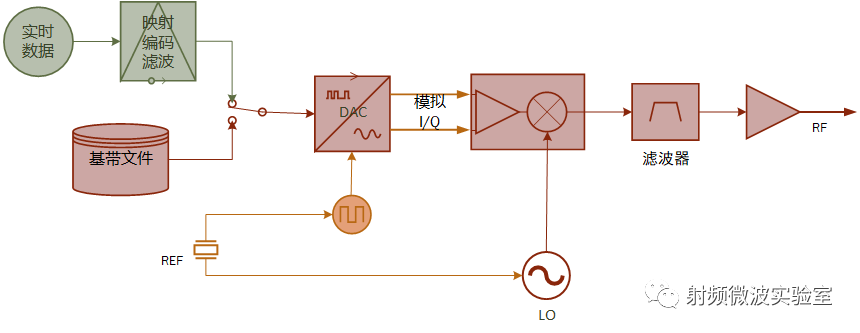
傻傻分不清?射頻模擬信號(hào)源和矢量信號(hào)源的區(qū)別

功率信號(hào)源的基本工作原理、用途和應(yīng)用方法
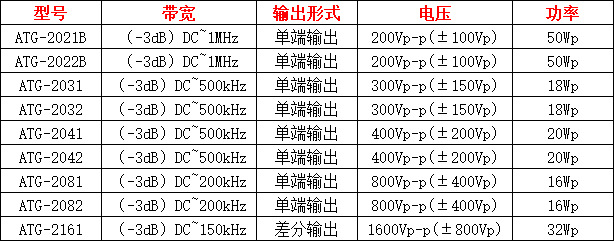
信號(hào)源功率輸出是什么意思(功率信號(hào)源)
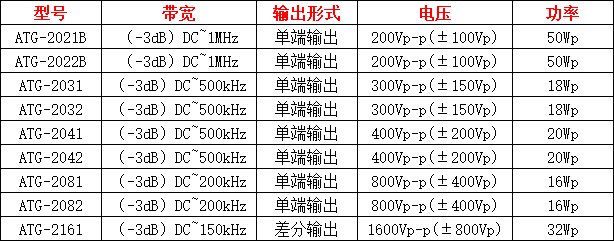
功率信號(hào)源是什么意思

射頻信號(hào)源的LF源與AM調(diào)制信號(hào)源是如何調(diào)試的呢?
安泰ATG-3090功率信號(hào)源的輸出信號(hào)是什么意思

Aigtek功率信號(hào)源的選型方法有哪些

ATG-3090功率信號(hào)源的使用方法有哪些






 關(guān)于相干信號(hào)源的處理方法
關(guān)于相干信號(hào)源的處理方法










評(píng)論