最近進(jìn)行代碼的review過程中看到同事在代碼中直接拿浮點(diǎn)數(shù)相等來作為條件，其他同事提醒他的時(shí)候，他還迷迷糊糊不知道為什么，所以就有了今天這篇文章。

1、浮點(diǎn)數(shù)據(jù)的不均勻

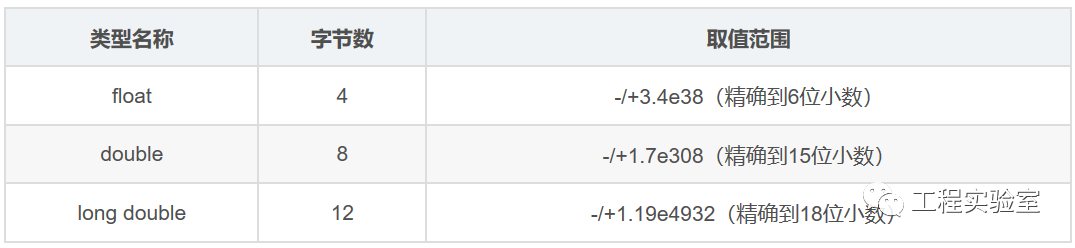
我們經(jīng)常會(huì)談到浮點(diǎn)數(shù)的精度問題，float-單精度，double-雙精度，double類型相比float類型精度更高，相應(yīng)的需要的內(nèi)存字節(jié)個(gè)數(shù)也越多，談到精度的問題，其實(shí)也就說明這種數(shù)據(jù)類型并不能夠連續(xù)的標(biāo)識任何的點(diǎn)，整形數(shù)就不用說了，小數(shù)部分直接不能標(biāo)識。

毒王這篇文章基本上可以從浮點(diǎn)數(shù)的存儲(chǔ)到表意來較好的認(rèn)識浮點(diǎn)數(shù)數(shù)據(jù)類型，但是中間部分對于浮點(diǎn)數(shù)精度部分的介紹并不是很形象，所以今天再詳細(xì)一點(diǎn)說明一下。

首先我們要認(rèn)識到通常float類型的變量占據(jù)四個(gè)字節(jié)，而uint32_t的整形類型也是占據(jù)四個(gè)字節(jié)，既然都是四個(gè)字節(jié)，那他們所能表示的不同數(shù)據(jù)個(gè)數(shù)是一樣的。

如果不太理解，可以把float看成4個(gè)bit，uint32_t也是4個(gè)bit，那么他們不管經(jīng)過什么變換，每個(gè)數(shù)據(jù)類型都只能夠標(biāo)識16個(gè)數(shù)。

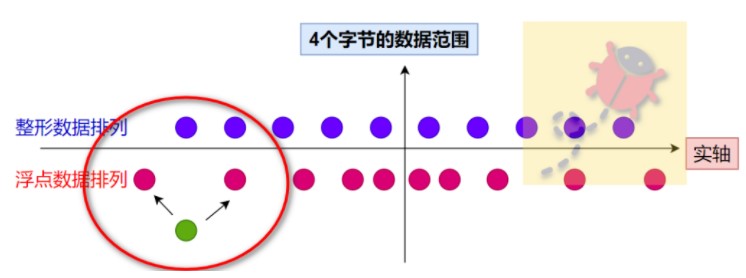
好，如下圖以4字節(jié)float的數(shù)據(jù)存儲(chǔ)模型所示:

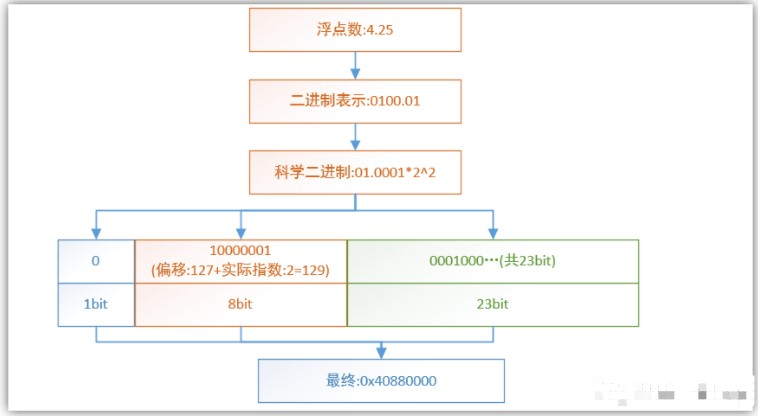
4個(gè)字節(jié)的浮點(diǎn)數(shù)，不像無符號整形所有的bit都是數(shù)據(jù)區(qū)，并且以每個(gè)數(shù)據(jù)之間相差1均勻分布，而浮點(diǎn)數(shù)把這4個(gè)字節(jié)分為了不同的區(qū)來起到不同的作用，從而用另外一種方式表達(dá)數(shù)據(jù)。

其指數(shù)部分越大，表示的數(shù)據(jù)就越大，但是尾數(shù)部分只能表示到23位，這樣的話導(dǎo)致數(shù)據(jù)的精度就越差，如果不太理解可以用一個(gè)較大的數(shù)通過上面的轉(zhuǎn)換方式進(jìn)行換算，便能理解。

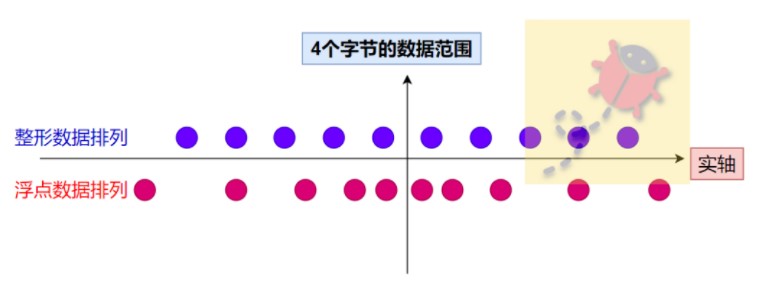
所以同樣是4個(gè)字節(jié)，根據(jù)浮點(diǎn)數(shù)的表示，越接近0就越稠密，越遠(yuǎn)離0就越稀疏，呈現(xiàn)一種不均勻的數(shù)據(jù)排列狀態(tài)，如上圖所示，同樣它也也不能標(biāo)識實(shí)軸上任意的點(diǎn)。

2、驗(yàn)證一下不均勻

好了，講了這么多理論，多多少少得來點(diǎn)程序驗(yàn)證一下:

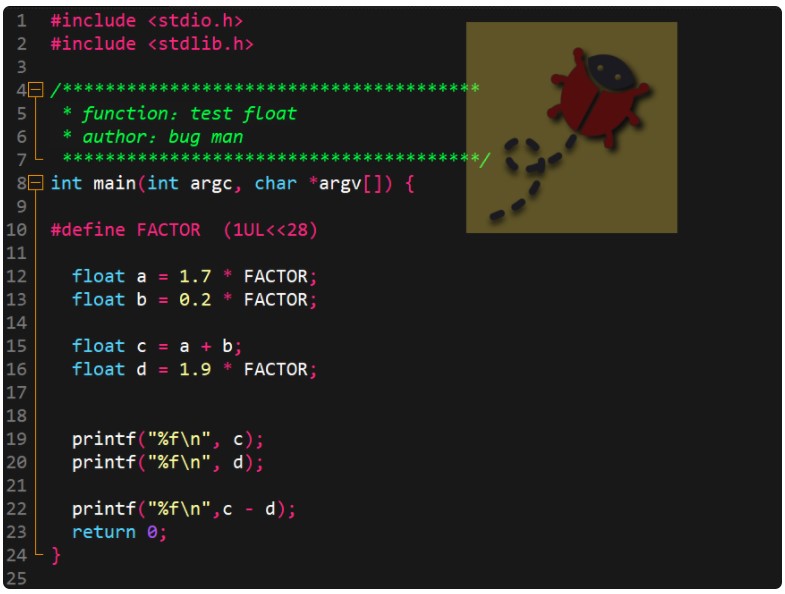
看看上面的代碼，這還用說，肯定這兩個(gè)數(shù)相等呀，相減也等于0，然而看一下輸出結(jié)果:

結(jié)果并不相等，并且相差還不少。

其結(jié)果也就說明了浮點(diǎn)數(shù)在大數(shù)的標(biāo)識精度不好，只能近似標(biāo)識，同時(shí)也說明了為什么一般不使用浮點(diǎn)數(shù)相等來進(jìn)行判斷的原因。

這也是為什么有時(shí)候明明我們采用直接編碼用準(zhǔn)確的浮點(diǎn)數(shù)，到了浮點(diǎn)數(shù)變量里面卻損失了精度，因?yàn)?個(gè)字節(jié)的float標(biāo)識不了，只能近似處理。

3、非要判斷相等

由于有些應(yīng)用非要使用浮點(diǎn)數(shù)進(jìn)行相等的處理，我們不應(yīng)該直接使用浮點(diǎn)數(shù)進(jìn)行等于號的判斷，而是要在一定的誤差和精度范圍內(nèi)進(jìn)行滿足。

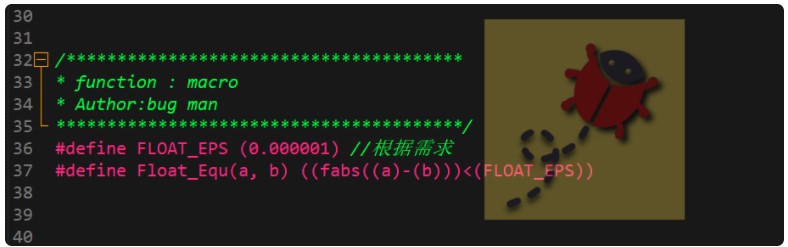
如上圖所示代碼是比較常用的處理辦法，在往期的文章中，bug菌沒有詳細(xì)的講解這個(gè)誤差宏的定義，前面了解到當(dāng)數(shù)據(jù)比較大的時(shí)候相鄰的差值會(huì)比較大，這樣就存在兩個(gè)浮點(diǎn)數(shù)的差值大于所設(shè)置的誤差范圍而無法判斷相等。

所以這樣的處理辦法來判斷浮點(diǎn)數(shù)近似相等會(huì)存在一些局限性。

那有沒有相對更好一點(diǎn)的辦法呢？

當(dāng)然是有的，不然接下來沒得寫了。

還是要從浮點(diǎn)數(shù)的存儲(chǔ)和標(biāo)識出發(fā)來處理該問題，既然浮點(diǎn)數(shù)天然就存在一定的誤差，而有時(shí)候計(jì)算又無法獲得唯一的數(shù)值，如下圖所示，浮點(diǎn)數(shù)計(jì)算出來的實(shí)軸上的值都會(huì)因?yàn)楦↑c(diǎn)數(shù)無法存儲(chǔ)標(biāo)識而近似到其相鄰的可以標(biāo)識的數(shù)值上。

從浮點(diǎn)的存儲(chǔ)模型來看，指數(shù)部分代表著浮點(diǎn)數(shù)的范圍，尾數(shù)部分代表著浮點(diǎn)數(shù)的精度，那么尾數(shù)的最后一位其實(shí)就表示了浮點(diǎn)數(shù)的當(dāng)前數(shù)值附近的精度。

于是對浮點(diǎn)的近似相等進(jìn)行了算法上的修改，如下代碼所示:

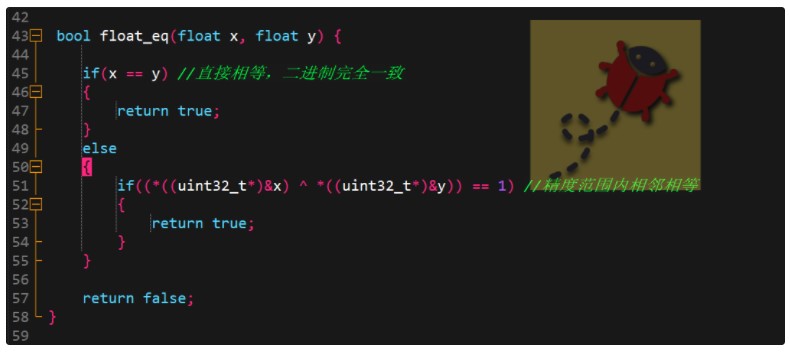
解釋一下 :

如果直接相等，說明浮點(diǎn)數(shù)各數(shù)據(jù)位都相等；而如果不相等可能相鄰，于是強(qiáng)制轉(zhuǎn)化為整形，比較尾數(shù)最后一位是否不同。

這里使用一個(gè)小技巧，采用異或的處理辦法，如果其他位都相同，而最后一位不同，結(jié)果就等于1，認(rèn)為兩個(gè)浮點(diǎn)數(shù)近似相等。

本文到此結(jié)束，我相信大家應(yīng)該對浮點(diǎn)數(shù)有了一個(gè)更加深入的了解，面對一些問題心中也會(huì)有一些答案，比如浮點(diǎn)數(shù)為什么不能作為switch的參數(shù)，也是同樣的原因。

但總的來說還是建議大家不要判斷浮點(diǎn)數(shù)相等，非要用也要特別小心。


審核編輯：劉清