巴特沃斯濾波器是一種有源濾波器，其通帶的頻率響應相對平坦。由于這種頻率響應，巴特沃斯濾波器也被稱為平坦濾波器。

使用巴特沃斯濾波器技術，可以設計所有類型的濾波器，包括高通、低通、帶通等。在本文當中，小編將重點介紹下使用巴特沃斯濾波器技術進行低通濾波器設計。

眾所周知，在設計濾波器電路時主要有三個考慮因素，它們是：

通帶的響應必須是最大平坦度

從通帶到阻帶必須有一個緩慢的過渡

濾波器在通帶內無任何失真地通過信號的能力。

通常情況下，這些失真通常是由波形的相移引起的。除了這三個，上升和下降時間參數也起著重要作用。所以，為了獲得最大的平坦響應，設計了巴特沃斯濾波器。而為了從通帶到阻帶的緩慢過渡，設計了切比雪夫濾波器，并設計了最大平坦時間延遲貝塞爾濾波器。

巴特沃斯濾波器

以從通帶到阻帶的過渡介質的陡度為代價，巴特沃斯濾波器將在輸出信號中提供平坦的響應。因此，它也被稱為最大平坦幅度濾波器。

濾波器的衰減響應速率由電路中的極數決定，極數將取決于電路中電抗元件的數量，即電路中使用的電感器或電容器的數量。

n階巴特沃斯濾波器的幅度響應如下：

V out / V in = 1 / √{1 + (f / f c ) 2n }

其中“n”是電路中的極數。隨著“n”值的增加，濾波器響應的平坦度也會增加。'f' = 電路的工作頻率，'f c ' = 電路的中心頻率或截止頻率。

這些濾波器具有預先確定的考慮，其應用主要用于較高頻率的有源RC電路。盡管它不提供尖銳的截止響應，但它通常被認為是在許多應用中使用的全能濾波器。

巴特沃斯濾波器近似值

為了滿足濾波器響應的考慮并獲得接近理想濾波器的近似值，需要具有更高階的濾波器，這將增加器復雜性。 此外，低通和高通電路具有輸出頻率響應和相位響應，所以理想的濾波器特性是最大平坦度、最大通帶增益和最大阻帶衰減。

要設計濾波器，需要適當的傳遞函數。為了滿足這些傳遞函數，在具有許多近似函數的模擬濾波器設計中進行了數學推導。

在此類設計中，巴特沃斯濾波器是其中一種濾波器類型，而低通巴特沃斯設計考慮主要用于許多功能。

一階低通巴特沃斯濾波器

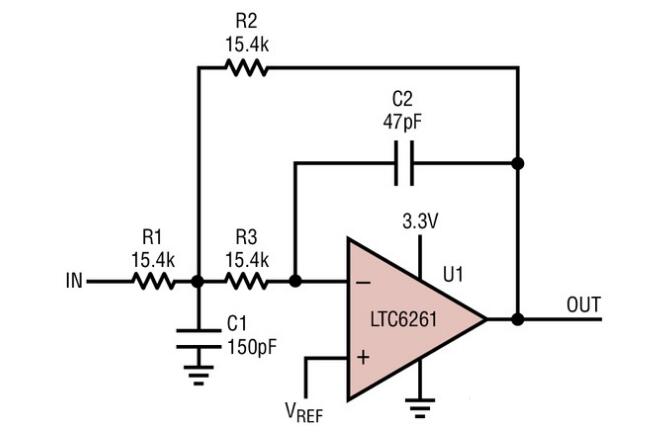
下面的電路顯示了低通巴特沃斯濾波器。

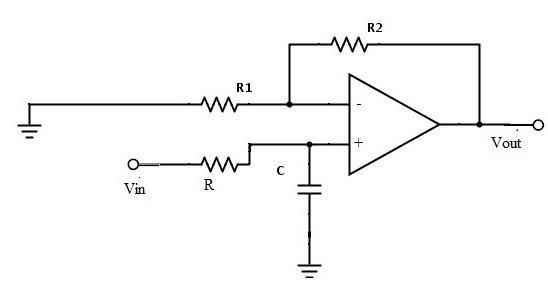
巴特沃斯濾波器所需的通帶增益主要取決于“R1”和“Rf”的電阻值，濾波器的截止頻率將取決于上述電路中的R和C元件。

濾波器的增益為：A_max=1+R1/Rf

電容器“C”的阻抗由-jX C 給出，電容器兩端的電壓為：

V c = – jX C / (R – jX C ) * Vin

其中XC = 1 / (2πfc)

極性形式的濾波器的傳遞函數為：

H(jω) = |Vout/Vin| ∟?

其中濾波器增益：V out / V in = A max / √{1 + (f/f H )2}，而相位角?= – tan -1 ( f/f H )

在較低頻率下意味著當工作頻率低于截止頻率時，通帶增益等于最大增益。

V out / V in = A max，即平衡常數。

在較高頻率下意味著當工作頻率高于截止頻率時，則增益小于最大增益。

Vout / Vin < Amax

當工作頻率等于截止頻率時，傳遞函數等于Amax /√2。增益的下降率為20dB/decade或者6dB/octave，可以在響應斜率中表示為-20dB/decade。

二階低通巴特沃斯濾波器

連接到一階巴特沃斯濾波器的附加RC網絡為我們提供了二階低通濾波器。這種二階低通濾波器的優點是增益在截止頻率之后在阻帶中滾降得非常快。

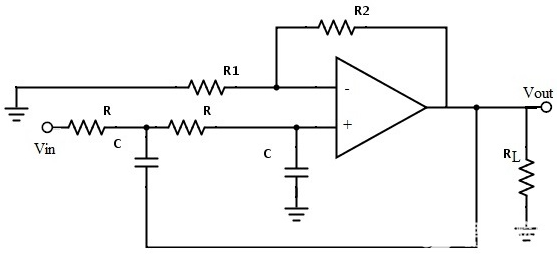
在這個二階濾波器中，截止頻率值取決于兩個RC部分的電阻和電容值。截止頻率使用以下公式計算：

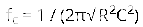
增益以40dB/decade的速率下降，該響應以斜率-40dB/decade顯示。濾波器的傳遞函數可以表示為：

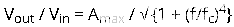
二階濾波器傳遞函數的標準形式為：

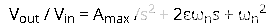
其中 ω n = 振蕩的固有頻率 =

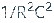
，ε = 阻尼系數 = (3 – A max ) / 2

對于二階巴特沃斯濾波器，所需的中間項是sqrt(2) = 1.414，從歸一化巴特沃斯多項式是：

3 – Amax = √2 = 1.414

為了確保輸出濾波器響應，增益Amax必須為 1.586。

通過級聯一階和二階巴特沃斯濾波器獲得高階巴特沃斯濾波器。這可以顯示如下：

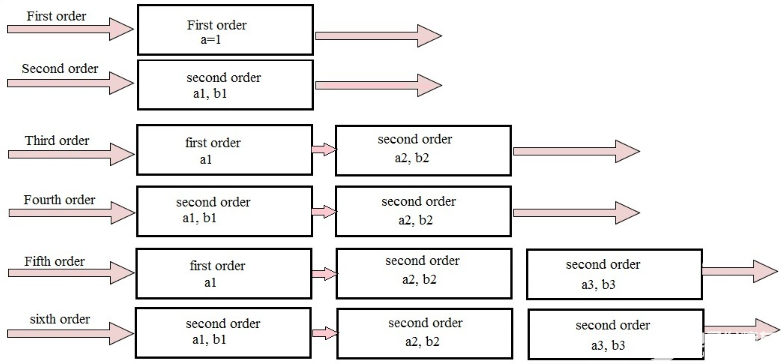
其中a n和b n 是預先確定的濾波器系數，它們用于生成所需的傳遞函數。

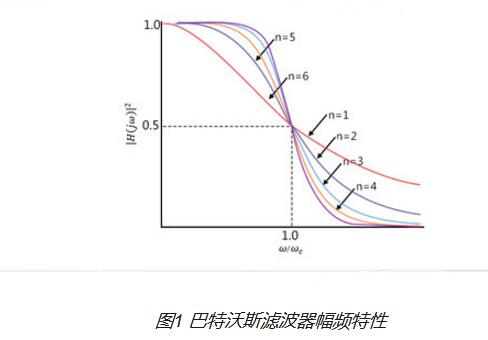
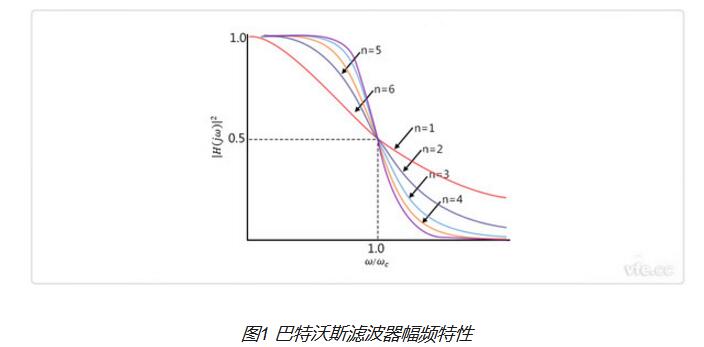
巴特沃斯濾波器的理想頻率響應

輸出響應的平坦度隨著濾波器階數的增加而增加，不同階數的巴特沃斯濾波器的增益和歸一化響應如下所示。

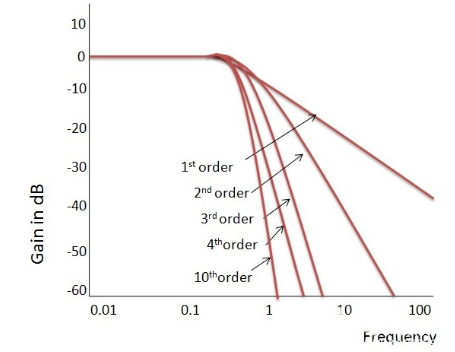
歸一化低通巴特沃斯濾波器多項式

歸一化是電壓、電流或阻抗除以相同測量單位的數量的過程，此過程用于生成特定值的無量綱范圍或水平。

濾波器傳遞函數的分母多項式為我們提供了巴特沃斯多項式。如果考慮一個以原點為中心的半徑相等的圓上的s平面，那么巴特沃斯濾波器的所有極點都位于該s平面的左半邊。

對于任何階濾波器，“s”的最高功率的系數應始終為1，對于任何階濾波器，常數項始終為1。對于偶數階濾波器，所有多項式因子本質上都是二次的。對于奇數階濾波器，除一階外，所有多項式都是二次的，對于一階濾波器，多項式為 1+s。

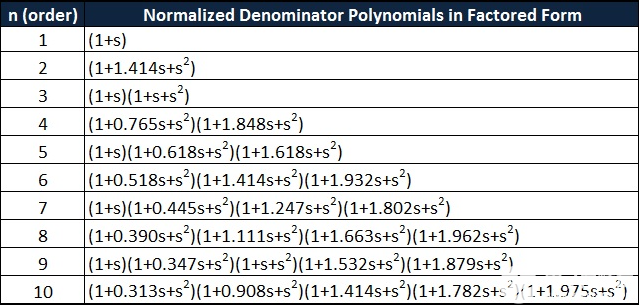
系數形式的巴特沃斯多項式如下表所示。

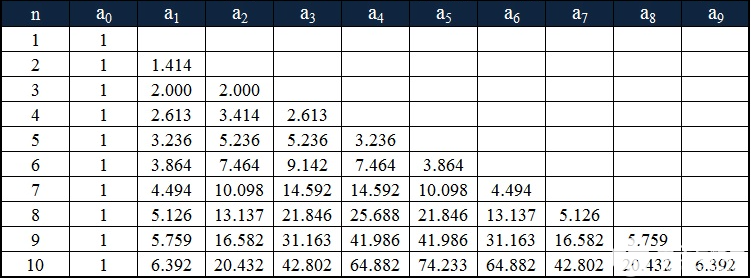
n階巴特沃斯濾波器的傳遞函數如下：

H (jω) = 1 / {{1 + ε2 (ω / ω c ) 2n }

其中n是濾波器的階數，ω是弧度頻率，它等于2πf，ε為最大通帶增益，即Amax。

三階巴特沃斯低通濾波器

一階和二階巴特沃斯濾波器的級聯連接給出了三階巴特沃斯濾波器，三階巴特沃斯濾波器電路如下圖所示。

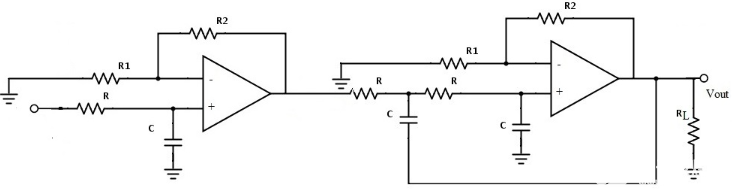
對于三階低通濾波器，給定的歸一化低通巴特沃斯多項式的多項式為 (1+s) (1+s+s2)，該濾波器包含三個未知系數，它們是 a 0、a 1、a 2。

它們的系數值為a 0 = 1、a 1 = 2 和a 2 = 2。與一階濾波器相比，該三階巴特沃斯濾波器的曲線平坦度增加。

巴特沃斯濾波器的應用

由于其最大平坦通帶特性，它在數據轉換器應用中用作抗混疊濾波器。

在雷達中有應用，例如設計雷達目標軌跡的顯示。

在高質量音頻應用中使用巴特沃斯濾波器。

用于運動分析的數字濾波器。

巴特沃斯低通濾波器示例

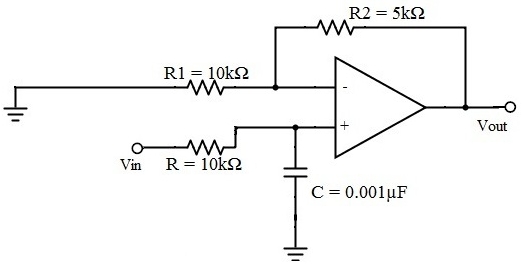
以截止頻率為15.9 kHz、通帶增益為1.5且電容器C=0.001μF的巴特沃斯低通濾波器為例：

fc = 1/2πRC

15.9 * 103 = 1 / {2πR1 * 0.001 * 10-6}

R = 10k?

Amax = 1.5，并假設R1=10 k?

Amax = 1 + {Rf / R1}

Rf = 5 k?

總結

巴特沃斯濾波器就是電子濾波器的一種，也被稱作最大平坦濾波器，其主要特點是通頻帶內的頻率響應曲線最大限度平坦，沒有紋波，而在阻頻帶則逐漸下降為零。

簡單來說，巴特沃斯濾波器是濾波器的一種設計分類，類同于切比雪夫濾波器，可以設計成高通，低通，帶通等多種濾波器。