了解ENOB（有效位數）的概念以及如何將其用于系統仿真中的數據轉換器建模。

在本系列的上一篇關于數據轉換器建模的文章中，我們討論了 模數轉換器型號討論了如何選擇用于實現模型的輸入信號的主題。 （請注意，這篇初始文章包括一個重要的縮寫、詞匯表和參考文獻列表。

在這里，我們將通過解決數據轉換器常用的一個品質因數，即“有效位數”或ENOB（［4］至［8］）來繼續討論。

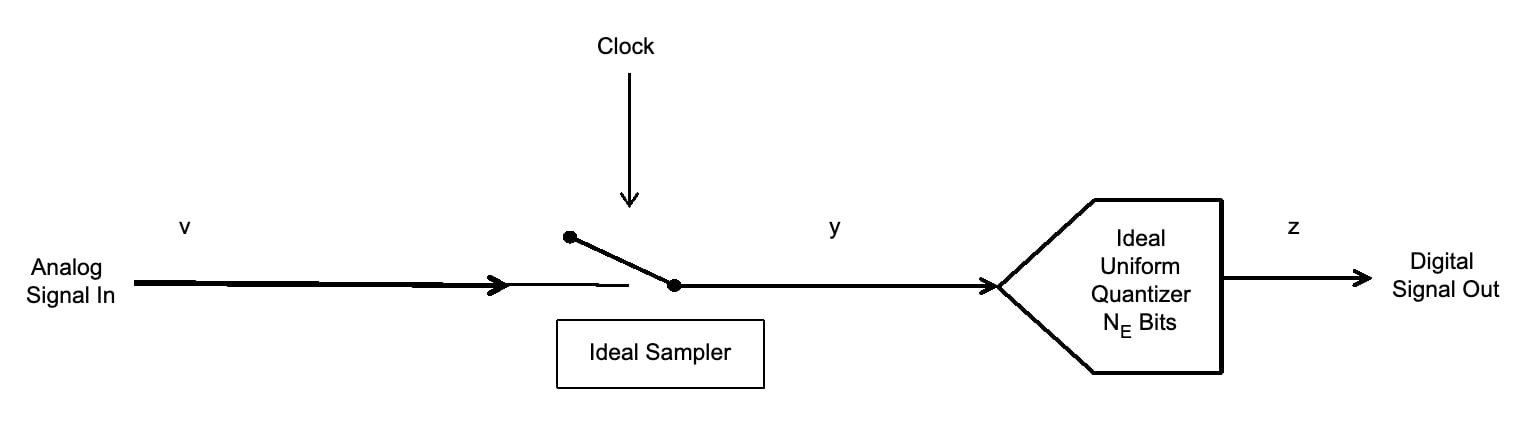
ENOB定義為理想量化器在相同條件下必須執行與數據轉換器相同的位數。 圖 1 所示的模型可以與 N 一起使用E = 伊諾布。

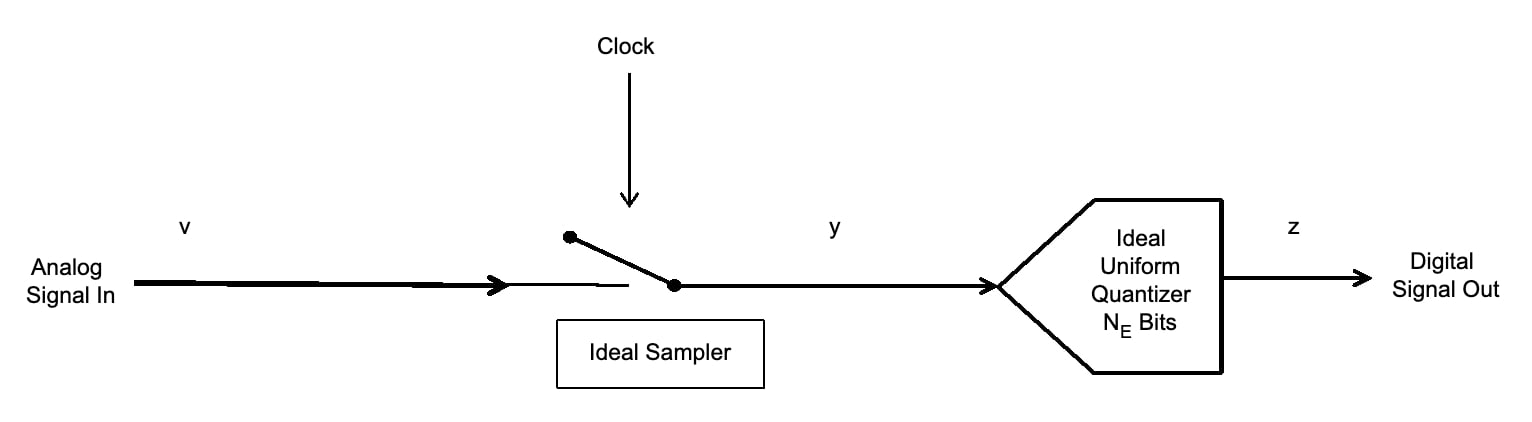
圖1. 模數轉換器的模型

問題出現了; “這些條件是什么，它們對于要使用的應用程序是否相同？ ENOB是否有不同的定義，應該用于不同的應用程序？

通常ENOB由給定頻率下的0 dB峰值FS正弦波輸入定義［8］。 它通常是頻率的函數。 讓LSB電壓為L，理想ADC有N位。

回到圖2，正弦波的峰值位于FS+ = L（（2N/2）-1） 和 FS- = ?L（2N/2）。

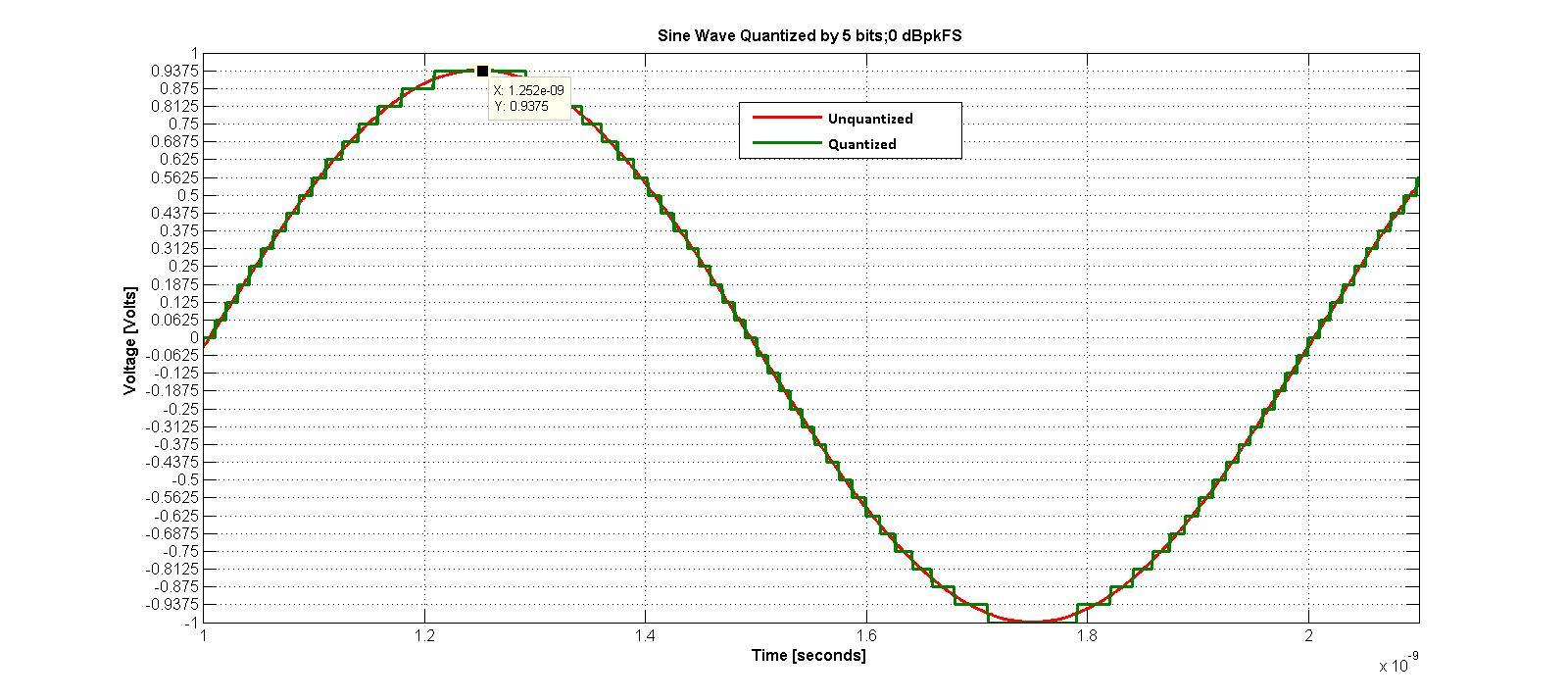
圖2. 圖 2 來自我們上一篇文章 如何為系統仿真對數據轉換器進行建模

對于 N ≥ 5; 假設 L（（2N/2）-1） = L（2N/2） 小于 7%，所以讓我們這樣做。 如果正弦波的峰值為 L（2N/2）; 其均方 （ms）
值為 L2（22N/8）。 眾所周知，對于理想ADC的隨機輸入，均方（ms）量化噪聲= L2/12（［2］，等式1.14）; 這是整個奈奎斯特區的噪聲（0 到F）。 但是我們有一個正弦波，而不是隨機輸入。 您的作者想知道相同的量化噪聲是否適用于正弦波以及ADC可能看到的其他輸入，因此進行了一些簡單的仿真。

結果如表1所示。

表 1.將不同波形的量化誤差均方放入量化器，無時間采樣

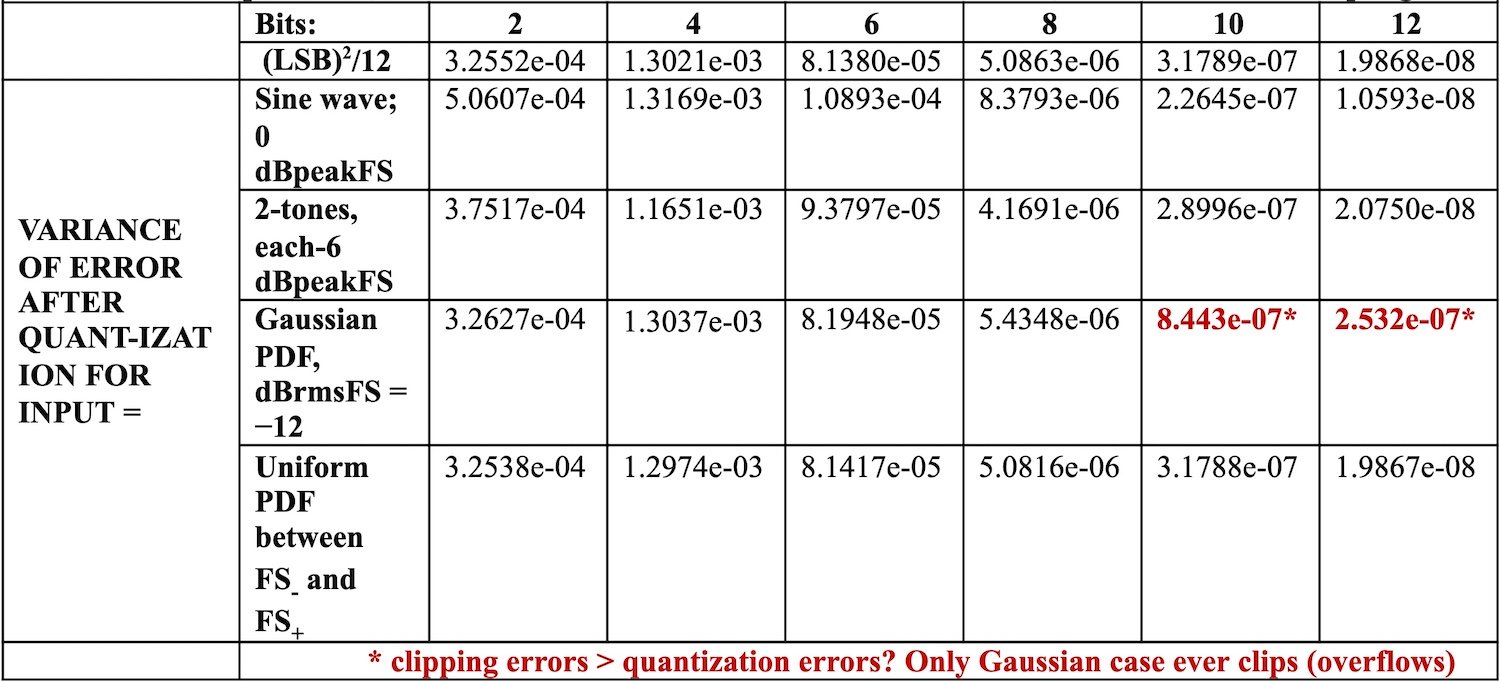
對于 2 到 12 位，均方噪聲使用公式 L2/12顯示; 并與各種輸入觀察到的均方噪聲進行比較。 即使對于單個正弦波，結果也相當接近。 唯一注意到差異的地方是高斯輸入，在–12dBrmsFS，10位和12位; 其中僅由量化引起的噪聲會很低。 然而，高斯噪聲的峰值會導致削波（過載），從而增加噪聲。

有趣的是，除了本文檔的.02版本中添加之外，Grey ［18A］得出了0 dBpeakFS正弦輸入的量化噪聲均方值的確切表達式：

其中 J0 是 0 階的普通貝塞爾函數。 對于大 x，J0（十） →0; 它是L2/12.}

因此，信噪比 （SNR）

SNR = ms(signal)/ms(noise) = (1.5)(2 ^2N^ )

或者，以dB為單位

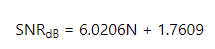
等式 1

仿真了一個由采樣器和理想N位量化器組成的ADC，表2顯示了5至12位的結果。 輸入正弦與ADC時鐘不同步。 結果非常接近公式1。

表 2.根據公式1和正弦波通過仿真ADC計算SNR

對于實際ADC，整個奈奎斯特區的信噪比和失真比（SINAD）在公式1中被替換為SNR，結果求解為N，現在稱為有效位數= NE.

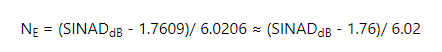
等式2

請注意，SINAD包括ADC的所有失真項，包括非線性引起的失真。 對于小于滿量程的輸入，ADC的失真會減小。 制造商通常會在某些輸入電平 –B dB峰值FS（峰值信號低于滿量程的 B dB）下測量 SINAD。 由于測試輸入信號比 B dB 低，因此它們將添加該值來計算ENOB，就好像失真不會因輸入較大而增加一樣。

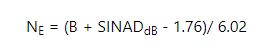
虛假方程

然而，這個等式是假的，因為它忽略了失真會增加的事實，通常比信號快。 對于簡單的三階非線性，信號每增加1 dB，失真就會增加3 dB，因此SINAD會差2dB。

因為互調非常重要，所以遵循我們 上一篇文章：應使用2音輸入信號。

還需要探索在整個奈奎斯特區和“相關帶寬”中測量噪聲和失真之間的差異。 圖3顯示了2音測試信號。

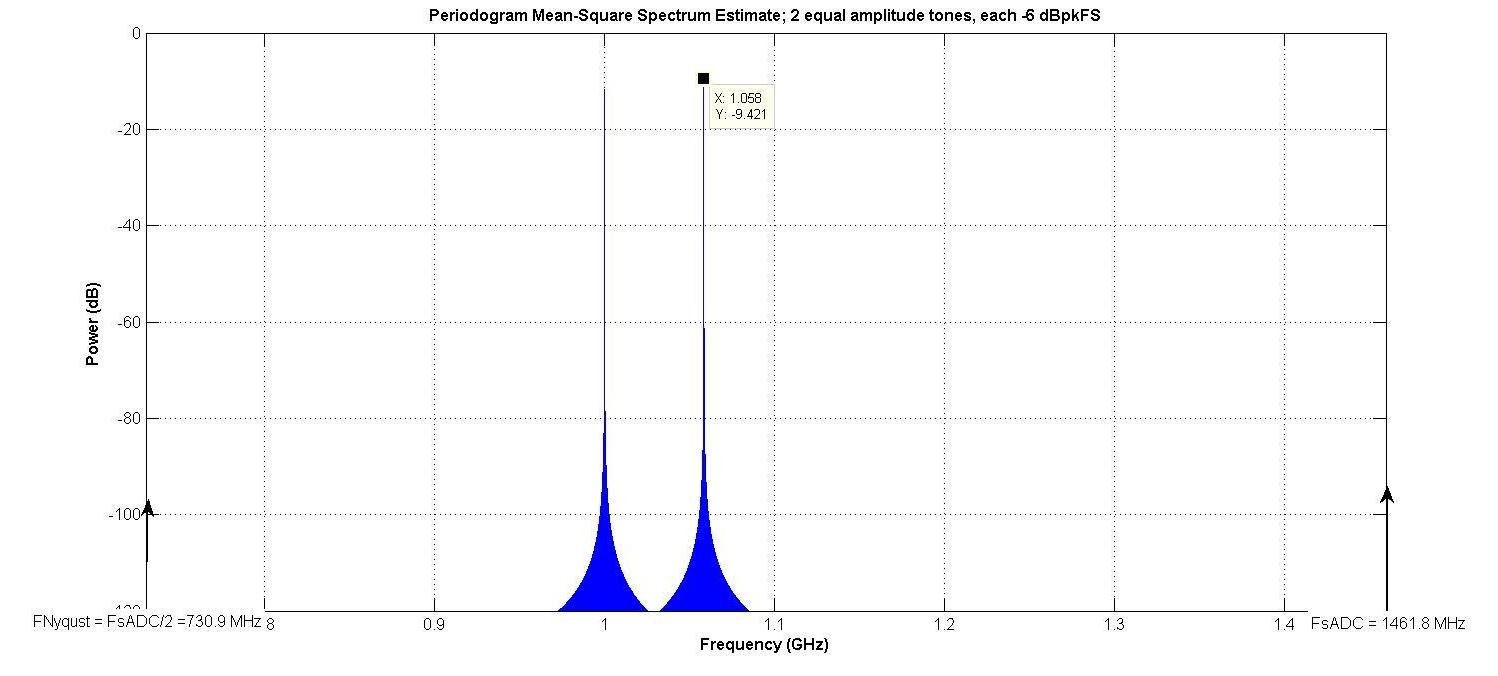
圖3.

由于 fS = 1461.8兆赫，f奈奎斯特 = 730.90兆赫。 因此，信號位于第二奈奎斯特區。 請注意，ADC的輸入可以劃分為奈奎斯特區。 由于ADC輸出是時間采樣的，因此不存在高于第一奈奎斯特區的頻率，因此僅稱為奈奎斯特區。

還使用了 1000 MHz 的 1 音測試信號。 “感興趣的帶寬”被任意定義為233.7 MHz，以兩個音調的中心為中心。 仿真了圖1的模型; 與 NE
是理想量化器中的位數。

圖4顯示了2音測試的輸出，其中對8位ADC進行了建模。 由于沒有明顯的雜散音（雜散），因此1音和2音輸入情況下的SINAD等于SNR。

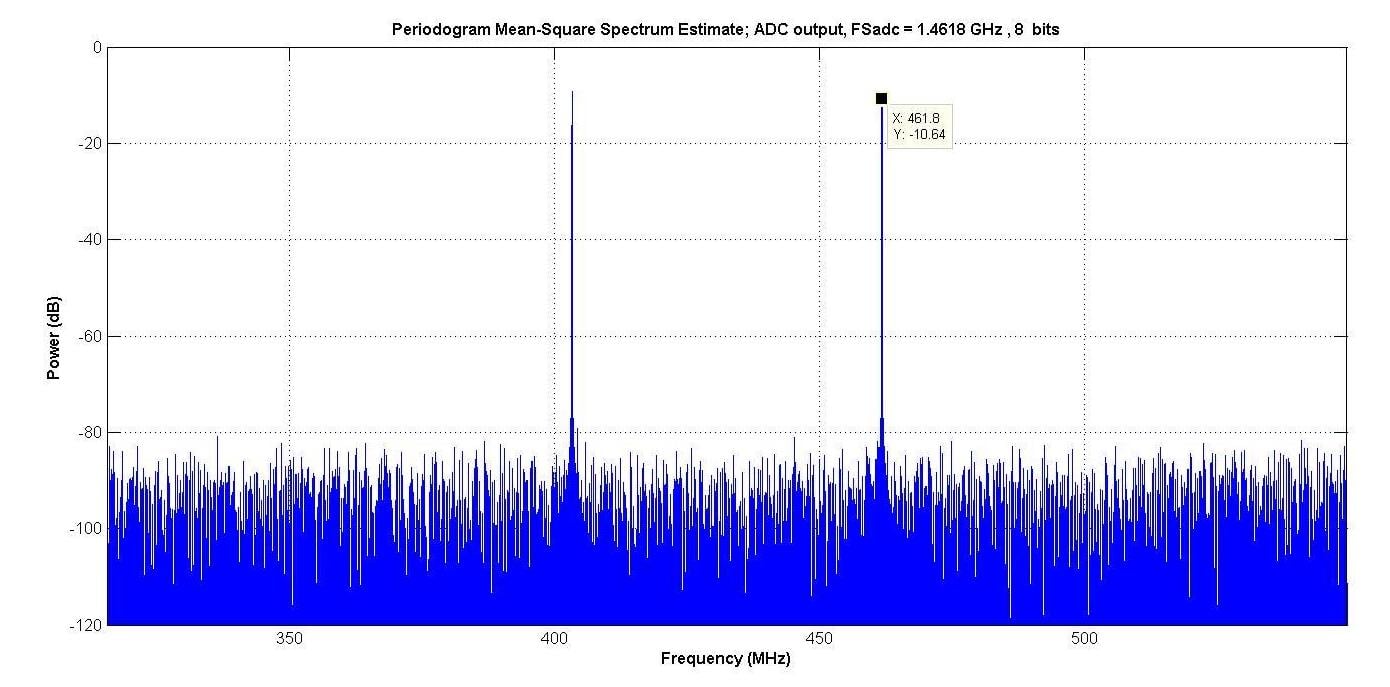
圖4.

當我們繪制以位函數確定的SINAD時，有兩個觀察結果。

首先，奈奎斯特帶寬和“相關帶寬”之間的差異是 3.1275; 相當于 4.95 dB。 因為這大約是奈奎斯特帶寬曲線與相同輸入的“相關帶寬”之間的差異; 這與量化噪聲頻譜為白色的假設一致。

其次，為了使峰值達到0 dB峰值FS，2音情況的平均功率必須是1音情況的1/2。 相同帶寬下，1 音和 2 音曲線之間的差異約為 3 dB。

它還顯示了與公式2的1音輸入的良好匹配。 可以定義兩種不同的 ENOB，將測量的 SINAD 與 1 音 （ENOB1） 和 2 音（ENOB2）
輸入

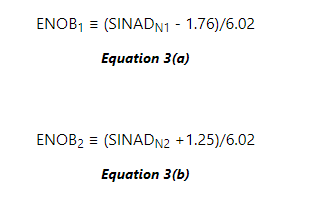
其中 SINAD鎳 是對于整個奈奎斯特帶寬，對于 i 輸入音，以 dB 為單位測量的 SINAD。 對于圖 1 的模型，兩個 ENOB 將相等。