對于一個離開課堂十余年的射頻工程師來說,傅里葉變換已經不知道埋藏在腦子里的那個角落,或者根本就沒在腦子里停留過。但無論如何,傅里葉變換對現在通信的重要性還是不言而語。當我們已經習慣用頻域去描述一個信號的時候,你可曾思考過其真實的樣子到底是什么?為什么這幾個短短的頻譜就可以描述一個信號?
所以呢,我們首先得感謝傅里葉,正是傅里葉大神的天才發明,帶給我們一個全新的看待問題的角度,讓我們跳出時域這個圈子,站在頻域的角度去看待問題。這樣做又有什么好處呢?且看下文。
首先來瞻仰一下傅里葉大神的肖像,致敬兩分鐘。(做好閱讀全文的心理準備)

其實傅里葉大神在最初提出這個思想的時候,并沒有想著去解決信號的問題,而是要來描述溫度的變化曲線,其實當時麥克斯韋也還沒有出生。傅里葉大神在1830年去世的時候,麥克斯韋還是是個躲在媽媽肚子里的小貝比呢。發明電話的那個亞歷山大貝爾還要再過十幾年才出生。所以,無心插柳柳成蔭吧。其實傅里葉變換除了在通信上有很重要的應用,在很多領域都有著不可替代的重要性。其作為一個數學工具,已經遍布現代科技的各個角落。傅里葉大神當時在法國科學學會上發表了一篇論文,這篇論文用正弦波來描述溫度變化曲線。如果只簡單描述溫度曲線的話也就罷啦,他出人意料的提出了一個在當時具有相當大的爭議性的論斷:任何連續周期信號可以由一組適當的正弦曲線組合而成。就像我們做選擇題一樣,太武斷的答案一定是錯的,所以當時人們也特別質疑過這個論斷,最著名的當屬兩個最著名的數學家拉格朗日和拉普拉斯。當時他們哥倆是傅里葉這篇論文的審稿人。所以說當時真是個神仙打架的時代。剛好在傅里葉大神的這篇論文審查時,拉格朗日和拉普拉斯兩位拉氏牛人就干起來了。拉普拉斯同意傅里葉的觀點,并同意發表這篇論文,而拉格朗日則堅決反對,因為拉格朗日堅決認為,傅里葉的方法無法表示帶棱角的信號。大家被高等數學里面拉格朗日的各種數學分析方法折磨,就知道,這個牛人我們惹不起,當時更沒人去挑戰拉格朗日的權威。因此這個論文就遲遲沒有發表。直到拉格朗日去世15年之后才公布于世。
不用說,現在傅里葉的論斷確實是正確的,為什么呢?因為老師說了,我們學了。那到底是不是這個回事呢?
我們先來看一下矩形信號能不能用一組適當的正弦曲線來組合而成?看下圖所示,一個正弦曲線時,和矩形差遠了。但是當疊加的正弦信號越來越多的時候,這個組合而來的圖形就越來越方了。當有無窮多個正弦曲線組合到一起的時候,這個組合圖就是矩形了。奇怪的是拉格朗日發明了無窮級數,怎么能沒想到這點呢?可能是屁股決定了腦袋。
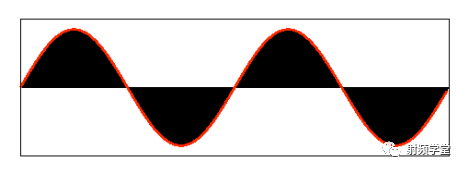
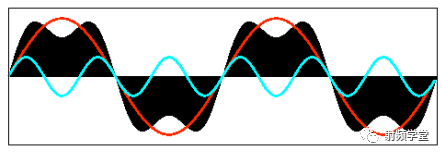
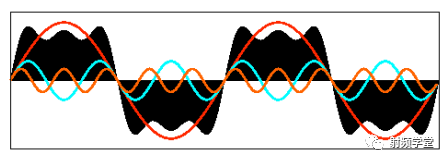
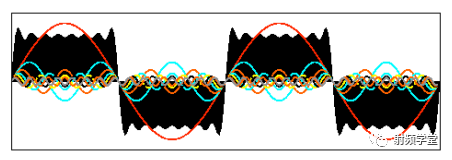
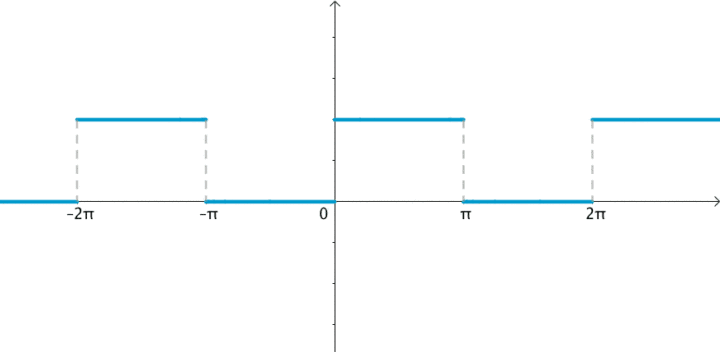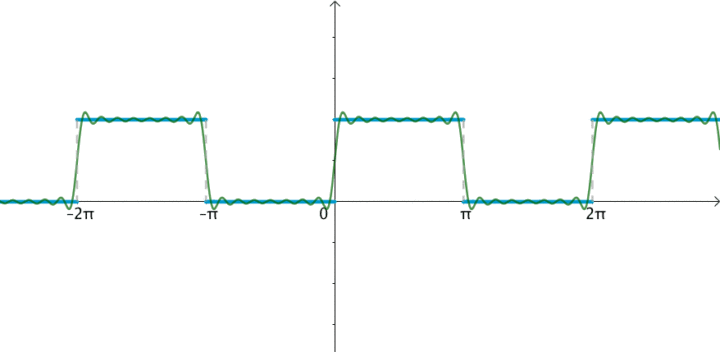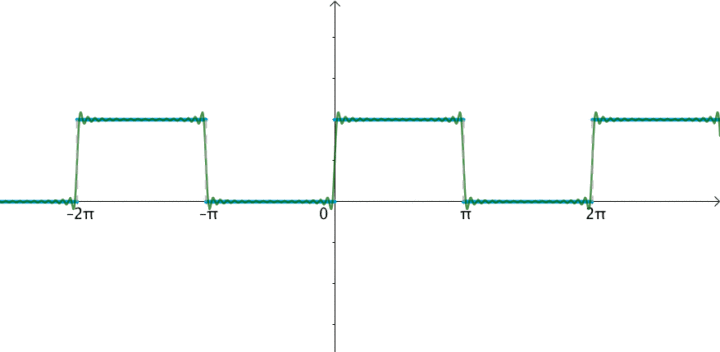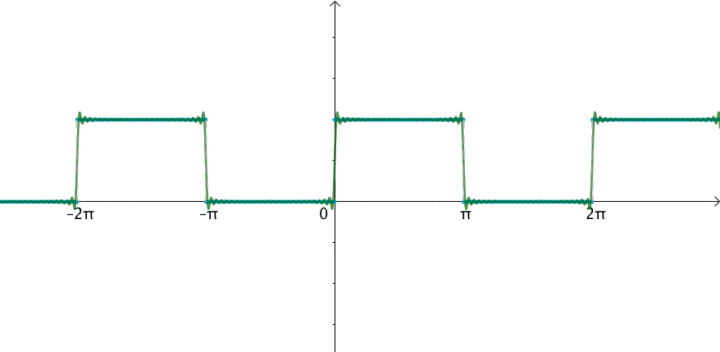
當然,人們對傅里葉的論斷又做了補充和擴展。傅里葉變換就是:
f(t)是t的周期函數,如果t滿足狄里赫萊條件:在一個以2T為周期內f(X)連續或只有有限個第一類間斷點,附f(x)單調或可劃分成有限個單調區間,則F(x)以2T為周期的傅里葉級數收斂,和函數S(x)也是以2T為周期的周期函數,且在這些間斷點上,函數是有限值;在一個周期內具有有限個極值點;絕對可積。
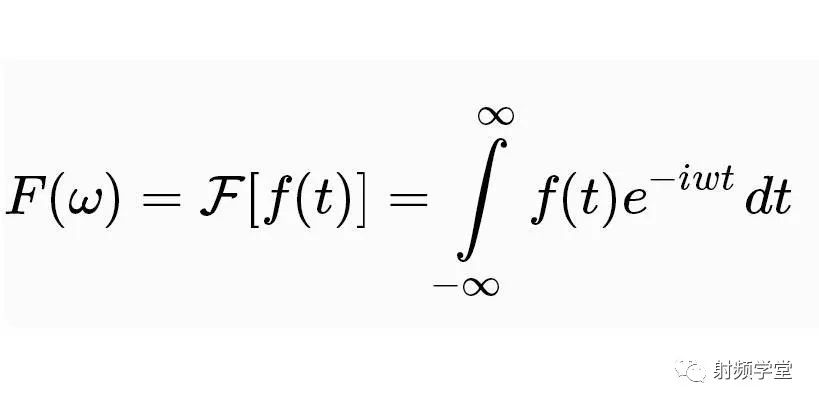
我們先把上面這個公式拋在腦后,接著講一下為什么是正弦曲線Sin(x)/余弦曲線?因為它簡單啊。它就是一個棍在轉圈圈。當一個點在繞著一個圓心做圓周運動時,其隨時間變化的曲線就是正弦曲線/余弦曲線。
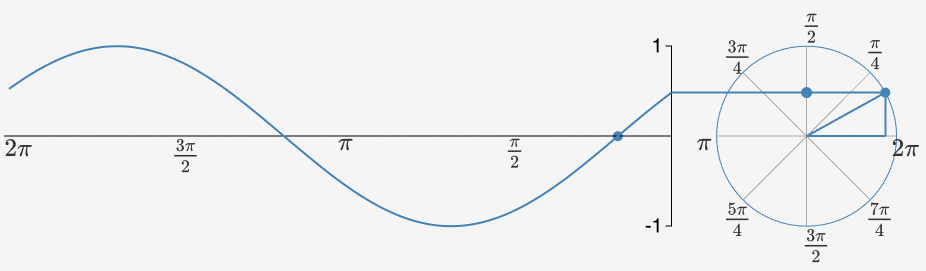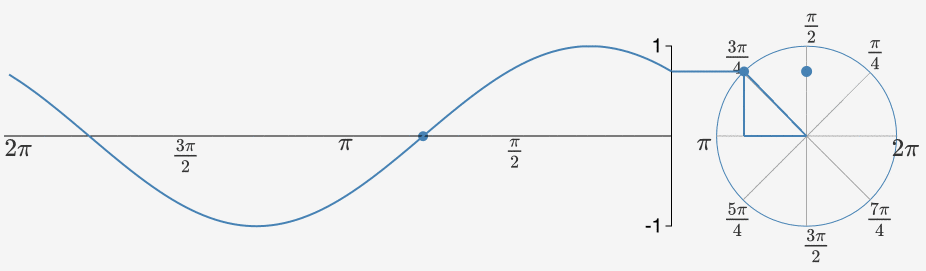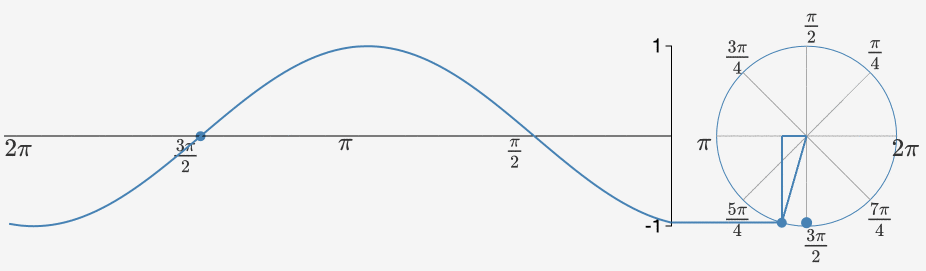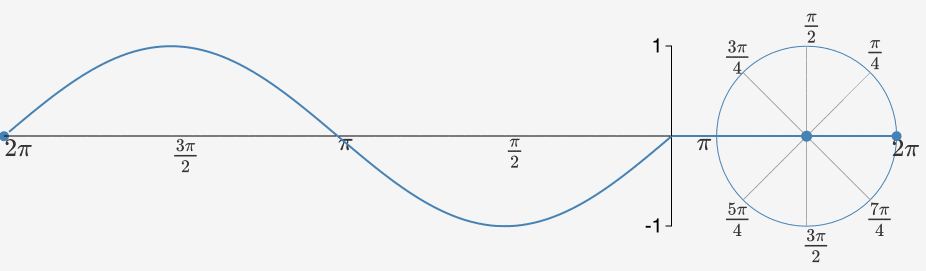
當我們把一組沿著不同圓周,不同圓心轉圈圈的點都拉到時間軸上來的時候,其就會變得越來越方。
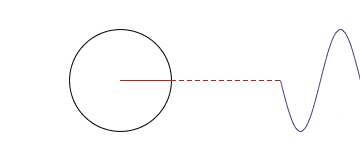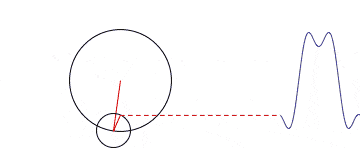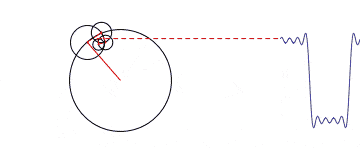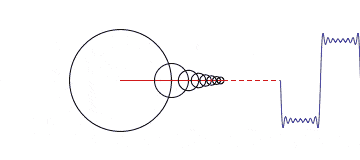
那跟頻域有什么關系呢?
好像有沒啥關系,這就是傅里葉級數吧。
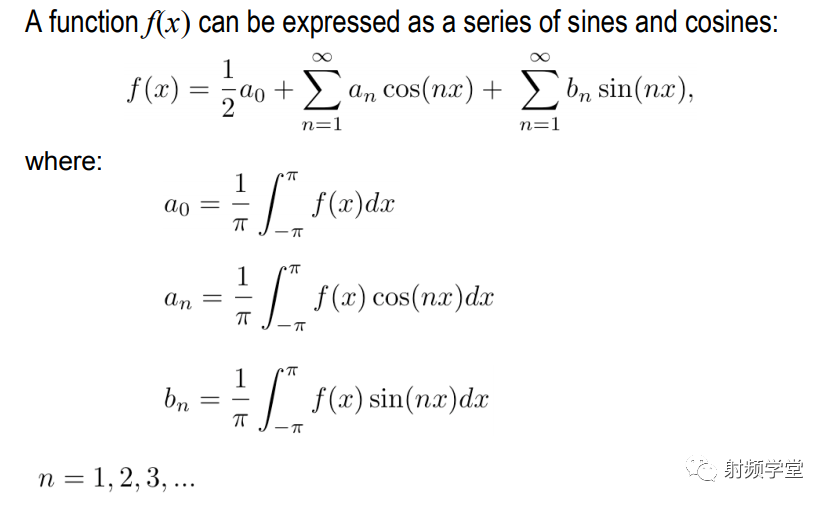
沒錯,就是傅里葉級數,但是把傅里葉級數的求和表示成積分形式就是傅里葉變換。
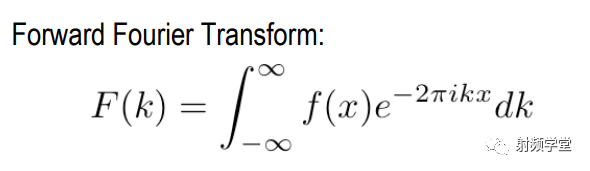
可能這里大家有點疑惑,上面傅里葉級數用的是三角函數Sin和Cos,但是下面的傅里葉變換卻換成了e的指數。原因有兩個,一是,太懶了,不想再編輯公式,第二個是感謝歐拉!歐拉統一了e的指數和正余弦函數:
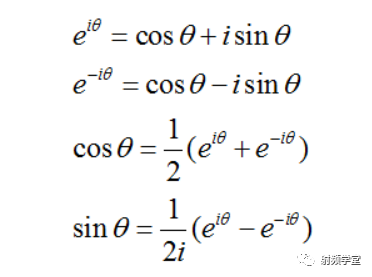
我們繼續研究上文的那個矩形曲線。我們把組成矩形曲線的這些正弦曲線鋪開放平,就可以觀察到它的頻域方向。從頻域方向看過去,就是一個個一定幅度的固定在某一頻率上的線。從頻域方向看過去,所有都靜止了,沒有時間了。也就是說,我們通過傅里葉變化,把信號從時域空間搬到了頻域空間。
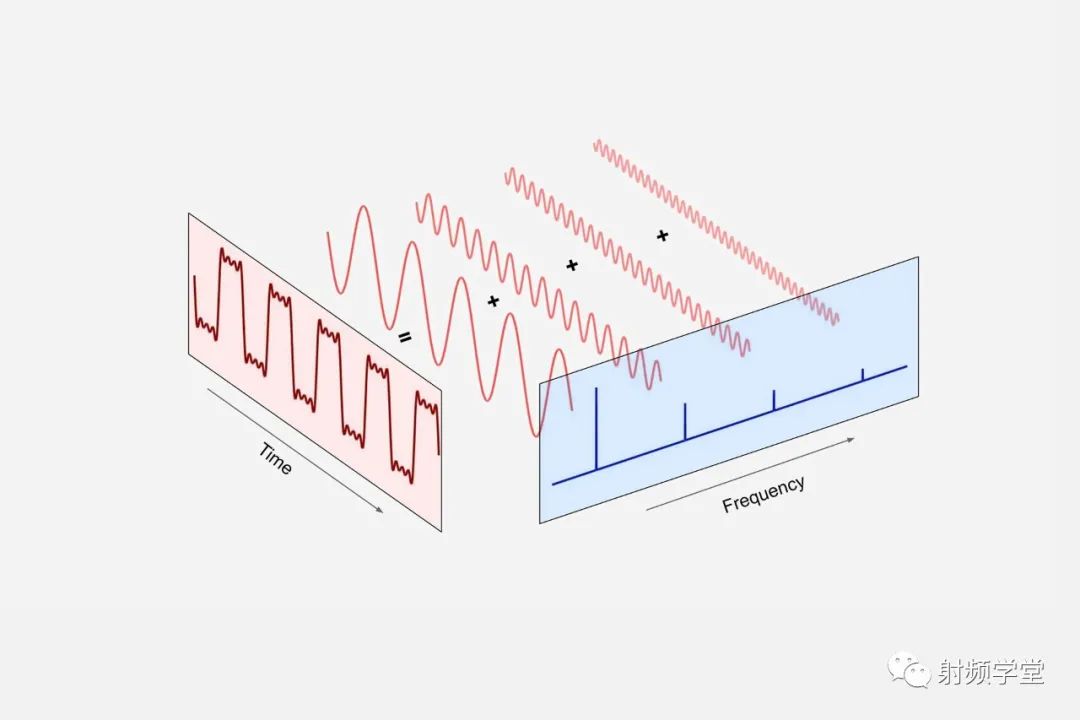
就像我們之前討論電磁波的三要素一樣,這個頻域信號也具有同樣的三要素:幅度,頻率和相位。幅度就是信號的強弱,或者是傅里葉級數里面的an,頻率就是里面的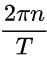 ,相位就是信號的初始位置。
,相位就是信號的初始位置。
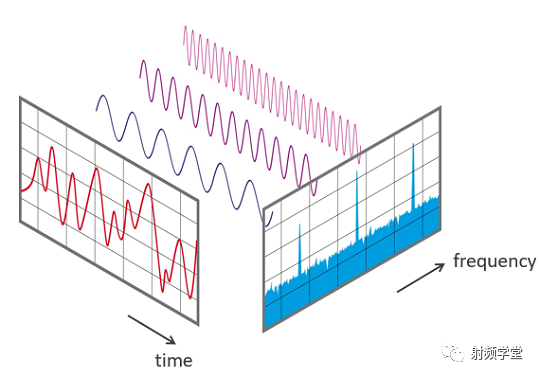
至此,我們就把信號從時域空間搬運到了頻域空間,而且兩個空間所描述的信號是一模一樣的,就像一個人有兩個名字一樣,劉備和劉玄德都是指的同樣一個人。頻域里的信號和時域里的信號一樣。所以,有時候分析一個信號,我們可以用頻譜分析儀去看它的頻譜,也可以用示波器去看它的波形一樣。
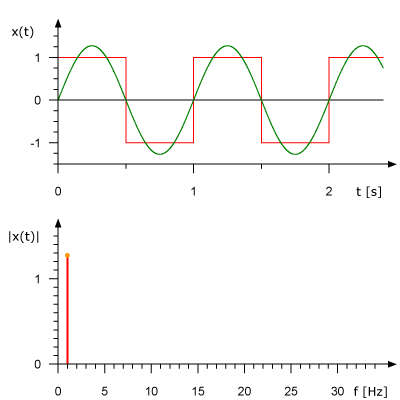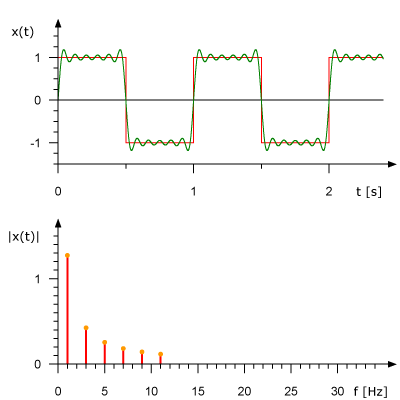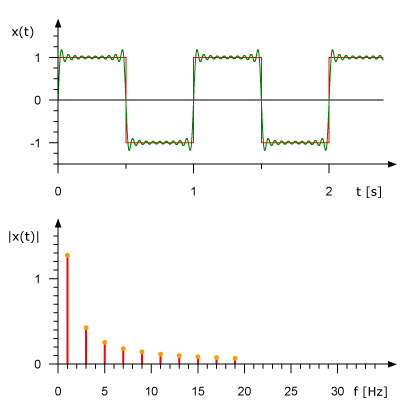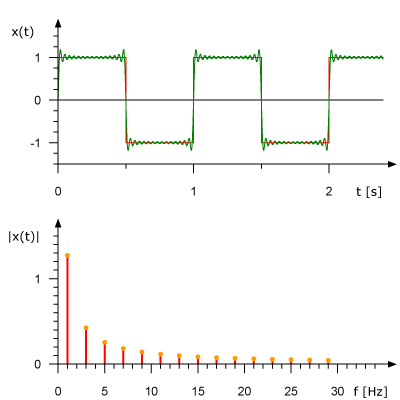
那么只要是滿足狄里赫萊條件的信號,都可以用傅里葉變換把其從時域變換到頻域。因為它都可以分解成一系列合適的正弦曲線的組合。
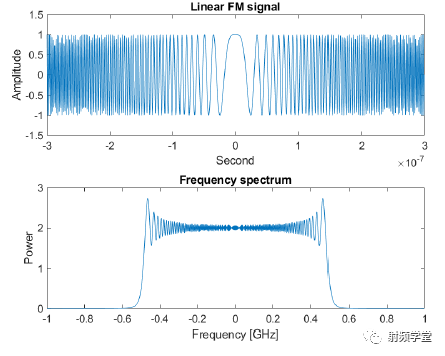
比如像FM調制的信號,其時域波形和頻譜如下圖所示。
審核編輯 :李倩
-
頻譜
+關注
關注
7文章
893瀏覽量
46276 -
函數
+關注
關注
3文章
4367瀏覽量
64062 -
傅里葉變換
+關注
關注
6文章
442瀏覽量
42991
原文標題:奇妙的傅里葉變換,原來是這樣子滴!
文章出處:【微信號:射頻學堂,微信公眾號:射頻學堂】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
VirtualLab:光柵的優化與分析
VirtualLab 應用:薄元近似(TEA)與傅里葉模態法(FMM)的光柵建模
ESP32P4小智AI演示
文丘里效應方程的應用






 傅里葉的論斷確實是正確的,為什么呢?
傅里葉的論斷確實是正確的,為什么呢?










評論