本文是決策樹的第三篇,主要介紹基于 Boosting 框架的主流集成算法,包括 XGBoost 和 LightGBM。
XGBoost

XGBoost 是大規模并行 boosting tree 的工具,它是目前最快最好的開源 boosting tree 工具包,比常見的工具包快 10 倍以上。Xgboost 和 GBDT 兩者都是 boosting 方法,除了工程實現、解決問題上的一些差異外,最大的不同就是目標函數的定義。故本文將從數學原理和工程實現上進行介紹,并在最后介紹下 Xgboost 的優點。
1.1 數學原理
1.1.1 目標函數
我們知道 XGBoost 是由 k 個基模型組成的一個加法運算式:
其中 為第 k 個基模型, 為第 i 個樣本的預測值。
損失函數可由預測值 與真實值 進行表示:
其中 n 為樣本數量。
我們知道模型的預測精度由模型的偏差和方差共同決定,損失函數代表了模型的偏差,想要方差小則需要簡單的模型,所以目標函數由模型的損失函數 L 與抑制模型復雜度的正則項 組成,所以我們有:
為模型的正則項,由于 XGBoost 支持決策樹也支持線性模型,所以這里不再展開描述。
我們知道 boosting 模型是前向加法,以第 t 步的模型為例,模型對第 i 個樣本 的預測為:
其中 由第 t-1 步的模型給出的預測值,是已知常數, 是我們這次需要加入的新模型的預測值,此時,目標函數就可以寫成:
求此時最優化目標函數,就相當于求解 。
泰勒公式是將一個在 處具有 n 階導數的函數 f(x) 利用關于 的 n 次多項式來逼近函數的方法,若函數 f(x) 在包含 的某個閉區間 上具有 n 階導數,且在開區間 (a,b) 上具有 n+1 階導數,則對閉區間 上任意一點 x 有 其中的多項式稱為函數在 處的泰勒展開式, 是泰勒公式的余項且是 的高階無窮小。
根據泰勒公式我們把函數 在點 x 處進行泰勒的二階展開,可得到如下等式:
我們把 視為 視為 ,故可以將目標函數寫為:
其中 為損失函數的一階導, 為損失函數的二階導,注意這里的求導是對 求導。
我們以平方損失函數為例:
則:
由于在第 t 步時 其實是一個已知的值,所以 是一個常數,其對函數的優化不會產生影響,因此目標函數可以寫成:
所以我們只需要求出每一步損失函數的一階導和二階導的值(由于前一步的 是已知的,所以這兩個值就是常數),然后最優化目標函數,就可以得到每一步的 f(x) ,最后根據加法模型得到一個整體模型。
1.1.2 基于決策樹的目標函數
我們知道 Xgboost 的基模型不僅支持決策樹,還支持線性模型,這里我們主要介紹基于決策樹的目標函數。
我們可以將決策樹定義為 ,x 為某一樣本,這里的 q(x) 代表了該樣本在哪個葉子結點上,而 w_q 則代表了葉子結點取值 w ,所以 就代表了每個樣本的取值 w (即預測值)。
決策樹的復雜度可由葉子數 T 組成,葉子節點越少模型越簡單,此外葉子節點也不應該含有過高的權重 w (類比 LR 的每個變量的權重),所以目標函數的正則項可以定義為:
即決策樹模型的復雜度由生成的所有決策樹的葉子節點數量,和所有節點權重所組成的向量的 范式共同決定。
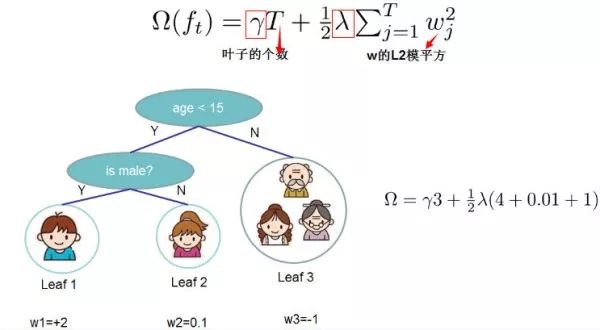
這張圖給出了基于決策樹的 XGBoost 的正則項的求解方式。
我們設 為第 j 個葉子節點的樣本集合,故我們的目標函數可以寫成:
第二步到第三步可能看的不是特別明白,這邊做些解釋:第二步是遍歷所有的樣本后求每個樣本的損失函數,但樣本最終會落在葉子節點上,所以我們也可以遍歷葉子節點,然后獲取葉子節點上的樣本集合,最后在求損失函數。即我們之前樣本的集合,現在都改寫成葉子結點的集合,由于一個葉子結點有多個樣本存在,因此才有了 和 這兩項, 為第 j 個葉子節點取值。
為簡化表達式,我們定義 ,則目標函數為:
這里我們要注意 和 是前 t-1 步得到的結果,其值已知可視為常數,只有最后一棵樹的葉子節點 不確定,那么將目標函數對 求一階導,并令其等于 0 ,則可以求得葉子結點 j 對應的權值:
所以目標函數可以化簡為:
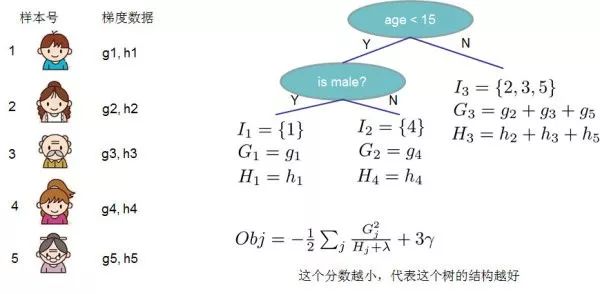
上圖給出目標函數計算的例子,求每個節點每個樣本的一階導數 和二階導數 ,然后針對每個節點對所含樣本求和得到的 和 ,最后遍歷決策樹的節點即可得到目標函數。
1.1.3 最優切分點劃分算法
在決策樹的生長過程中,一個非常關鍵的問題是如何找到葉子的節點的最優切分點,Xgboost 支持兩種分裂節點的方法——貪心算法和近似算法。
1)貪心算法
- 從深度為 0 的樹開始,對每個葉節點枚舉所有的可用特征;
- 針對每個特征,把屬于該節點的訓練樣本根據該特征值進行升序排列,通過線性掃描的方式來決定該特征的最佳分裂點,并記錄該特征的分裂收益;
- 選擇收益最大的特征作為分裂特征,用該特征的最佳分裂點作為分裂位置,在該節點上分裂出左右兩個新的葉節點,并為每個新節點關聯對應的樣本集
- 回到第 1 步,遞歸執行到滿足特定條件為止
那么如何計算每個特征的分裂收益呢?
假設我們在某一節點完成特征分裂,則分列前的目標函數可以寫為:
分裂后的目標函數為:
則對于目標函數來說,分裂后的收益為:
注意該特征收益也可作為特征重要性輸出的重要依據。
對于每次分裂,我們都需要枚舉所有特征可能的分割方案,如何高效地枚舉所有的分割呢?
我假設我們要枚舉所有 x < a 這樣的條件,對于某個特定的分割點 a 我們要計算 a 左邊和右邊的導數和。
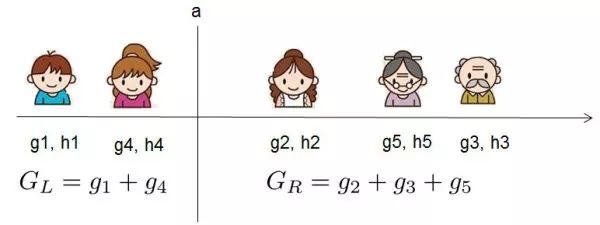
我們可以發現對于所有的分裂點 a,我們只要做一遍從左到右的掃描就可以枚舉出所有分割的梯度和 和 。然后用上面的公式計算每個分割方案的分數就可以了。
2)近似算法
貪婪算法可以的到最優解,但當數據量太大時則無法讀入內存進行計算,近似算法主要針對貪婪算法這一缺點給出了近似最優解。
對于每個特征,只考察分位點可以減少計算復雜度。
該算法會首先根據特征分布的分位數提出候選劃分點,然后將連續型特征映射到由這些候選點劃分的桶中,然后聚合統計信息找到所有區間的最佳分裂點。
在提出候選切分點時有兩種策略:
- Global:學習每棵樹前就提出候選切分點,并在每次分裂時都采用這種分割;
- Local:每次分裂前將重新提出候選切分點。
直觀上來看,Local 策略需要更多的計算步驟,而 Global 策略因為節點沒有劃分所以需要更多的候選點。
下圖給出不同種分裂策略的 AUC 變換曲線,橫坐標為迭代次數,縱坐標為測試集 AUC,eps 為近似算法的精度,其倒數為桶的數量。
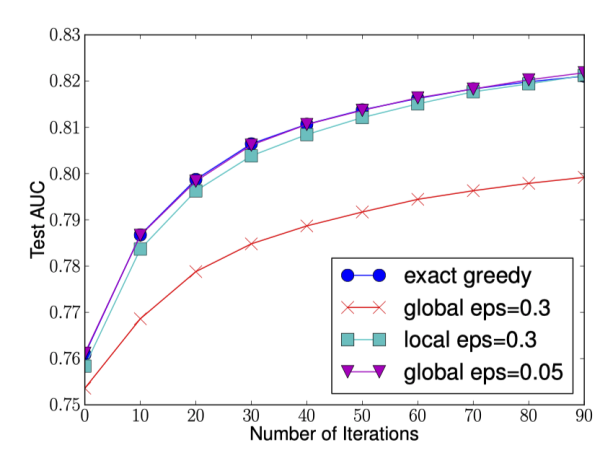
我們可以看到 Global 策略在候選點數多時(eps 小)可以和 Local 策略在候選點少時(eps 大)具有相似的精度。此外我們還發現,在 eps 取值合理的情況下,分位數策略可以獲得與貪婪算法相同的精度。

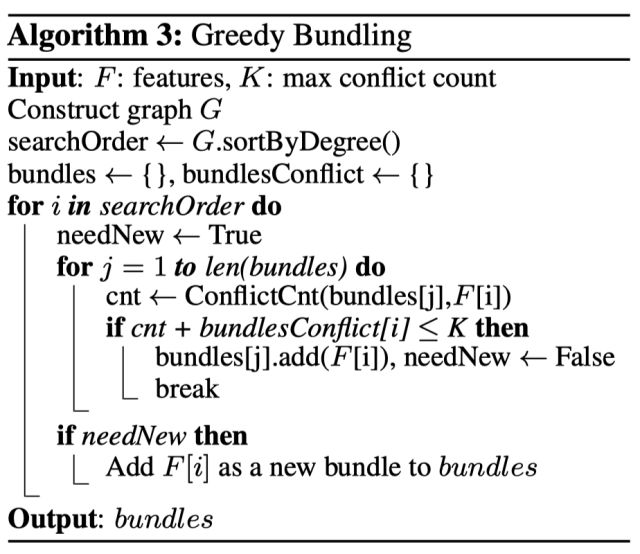
- 第一個 for 循環:對特征 k 根據該特征分布的分位數找到切割點的候選集合 。XGBoost 支持 Global 策略和 Local 策略。
- 第二個 for 循環:針對每個特征的候選集合,將樣本映射到由該特征對應的候選點集構成的分桶區間中,即 ,對每個桶統計 G,H 值,最后在這些統計量上尋找最佳分裂點。
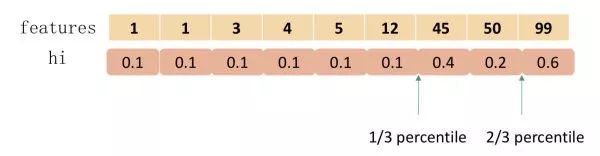
下圖給出近似算法的具體例子,以三分位為例:
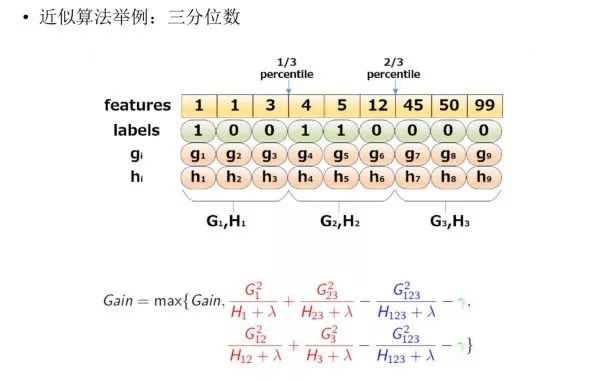
根據樣本特征進行排序,然后基于分位數進行劃分,并統計三個桶內的 G,H 值,最終求解節點劃分的增益。
-
機器學習
+關注
關注
66文章
8477瀏覽量
133803 -
決策樹
+關注
關注
3文章
96瀏覽量
13728
發布評論請先 登錄
相關推薦
五步直線掃描轉換生成算法
基于OFDM系統的時域頻域波束形成算法

基于加權co-occurrence矩陣的聚類集成算法





 基于 Boosting 框架的主流集成算法介紹(上)
基于 Boosting 框架的主流集成算法介紹(上)











評論