這篇文章來源于DevicePlus.com英語網站的翻譯稿。

在第3部分中，我們的目標是了解如何將正弦信號從時域轉換到頻域。這個操作過程很重要，因為您可以以此了解在頻率范圍內可以確定多少信息。例如，ECG（心電圖）中如果僅有時域信號，信息量是不夠的，因為它只包含了隨時間變化的心跳記錄（即信號）。但是，在ECG中補充頻域分析就能夠提供一段時間內信號幅度變化發生次數的有關信息。頻域信息以此方式展示了在一定頻率范圍內，信號在每個給定的頻率帶是如何分布的。使用傅里葉變換（FT）可以完成時域和頻域之間的信號轉換。

硬件

? Arduino Uno

? 用于Arduino的MAX9812L駐極體麥克風傳感器板

軟件

Arduino IDE

MATLAB

步驟 1：傅里葉變換簡介

我們首先了解一下相關定義。信號是“傳遞某種現象的行為或屬性信息的一種函數。” 時域表示信號的幅度是如何隨時間變化的，而頻域則表示隨頻率變化的幅度頻。讓我們再次看一下心電圖（ECG）示例。心電圖顯示的是重復的信號波，可以觀察到這些信號波的特征是如何隨時間變化的（即信號是如何演化的）。很難對一段較長時間內記錄的ECG的每個重要成分都進行分析。在這種情況下，您可以將信號轉換到頻域，并觀察在特定時間間隔內重復的每個分量。這就是傅里葉變換的來歷。

FT也會在圖像和視頻壓縮中用到。例如，jpg 和 mp3是使用了快速傅里葉變換（FFT）算法的圖像和聲音的數字格式。由于必須使用模數轉換器將每個連續的模擬信號轉換為數字信號，所以需要以特定頻率對這些信號進行采樣。這樣，我們可以利用離散傅里葉變換獲取離散信號。

傅里葉級數的有趣之處在于，每個波形都可以寫成正弦和余弦的總和，但是具有離散頻率分量。使用TF，我們可以將波形分解為正弦波。

讓我們看一下由多個正弦波組成的信號。該圖顯示了一個來自現實世界的具有多個頻率分量的信號：

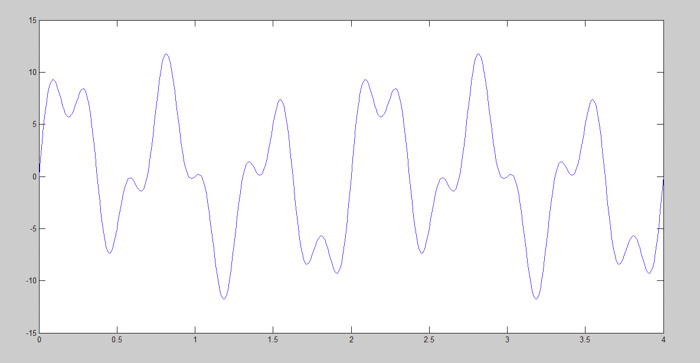
圖1：初始信號

我們將會通過下面的所有步驟來逐步添加正弦波，以確定該信號是如何形成的。

f1 = 1;
f2 = 0.5;
f3 = 1.5;
f4 = 4;
t = 0:0.01:4;
A1 = 0.5;
A2 = 2.5;
A3 = 7.5;
A4 = 3.5;

x1 = A1*sin(2*pi*f1*t)
x2 = A2*sin(2*pi*f2*t)
x3 = A3*sin(2*pi*f3*t)
x4 = A4*sin(2*pi*f4*t)

x = x1 + x2+ x3+ x4

添加到圖形中的第一個信號如下：

figure %Figure 2
subplot(2,1,1)
plot(t,x,t,x1)
subplot(2,1,2)
plot(t,x1)

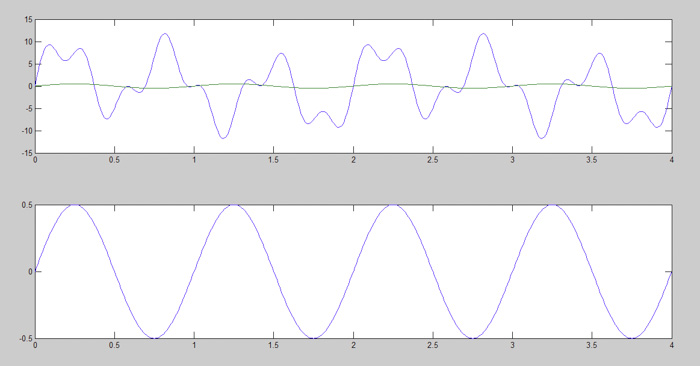
圖2：形成圖1信號的第1步

在圖2中，正弦波（底部）被繪制在初始信號（頂部）中。初始信號還包含許多其它信號。我們將嘗試獲取頂部圖形中的藍色信號，證明任何信號都可以表示為一些正弦信號之和。

figure %Figure 3
subplot(3,1,1)
plot(t,x,t,x1+x2)
subplot(3,1,2)
plot(t,x2)
subplot(3,1,3)
plot(t,x1+x2)

以下信號應該盡可能接近原始信號。在隨后的每個圖中將具有以下三個子圖：

1.subplot(3,1,1)：在同一坐標圖中繪制兩個圖形，藍色表示初始信號，由不同頻率的正弦波疊加而成，綠色表示獲得原始信號之前的所有步驟中所添加信號的總和。

2.subplot(3,1,2)：當前步驟中所添加的信號，由另一個幅度和頻率來表達。

3.subplot(3,1,3)：信號總和 – subplot(3,1,1) 中的綠色信號，沒有重疊部分。

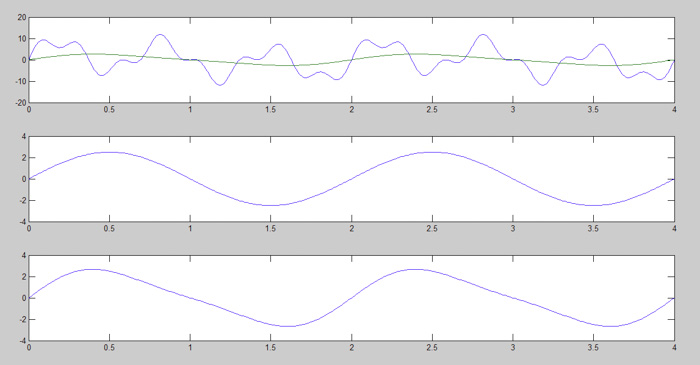
圖3：形成初始圖像的第2步

從圖3中可以看出，信號已經開始形成初始信號的波形。在subplot(3,1,3)中，您可以觀察到形狀由于添加了更多的信號而發生了變化。從這一步開始，信號不再是標準的正弦曲線形狀。

figure %Figure 4
subplot(3,1,1)
plot(t,x,t,x1+x2+x3)
subplot(3,1,2)
plot(t,x3)
subplot(3,1,3)
plot(t,x1+x2+x3)

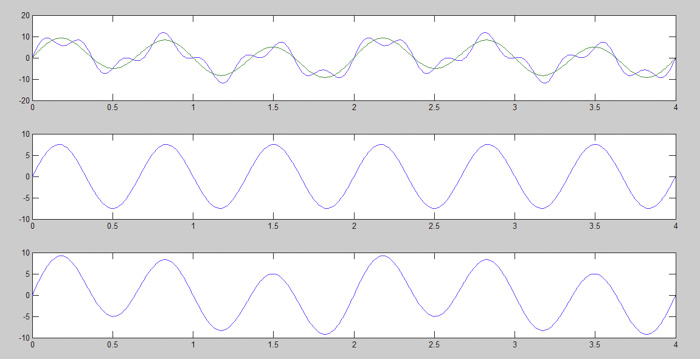
圖4：形成原始信號的第3步

在圖4中，我們可以觀察到subplot (3,1,3)的信號幅度是如何演變的。A3 = 7.5 表明，當添加多個信號時，所得信號的幅值是由每個信號的幅值相加得到的。

figure %Figure 5
subplot(3,1,1)
plot(t,x,t,x1+x2+x3+x4)
subplot(3,1,2)
plot(t,x4)
subplot(3,1,3)
plot(t,x1+x2+x3+x4)

在正弦信號相加過程的最后一步中，演示了原始信號是如何形成的。最后添加的信號相比于上一步中添加的信號具有更高的頻率。與上圖相比，我們可以觀察到圖5中的subplot(3,1,3)包含更多的曲線波形。

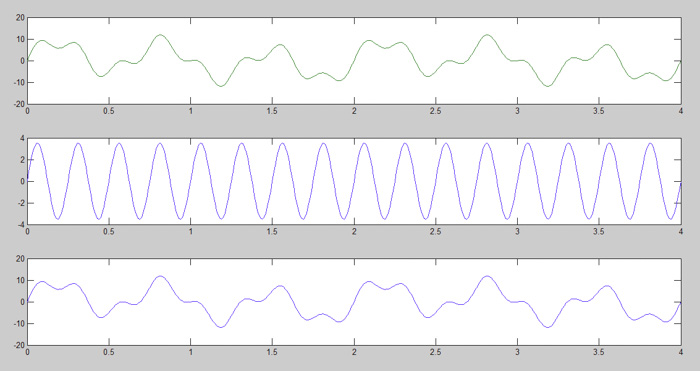
圖5：形成原始信號的最后一步

如圖5所示，subplot(3,1,1)的綠色信號與subplot(3,1,3)的藍色信號之間沒有任何區別。該示例很重要，因為它展示了傅里葉級數的邏輯，即將一個信號可以描述為不同頻率正弦波之和。

傅里葉變換被用于那些需要在頻域中執行的操作（例如濾波）。在頻域中獲得結果后，我們可以將信號轉換回時域，以便于在后續處理中使用。

步驟2：背后的算法

復數是傅里葉變換算法中的一個重要概念。復數可以表示為z = a + bi，其中a & b為實數，i是虛數，為x2-1的解（因為該式沒有實數解，所以解被認為是虛數）。

下圖顯示了如何用圖形表示復數。您可以通過Argand 圖對復數進行幾何表示。x軸表示復數的實部，y軸表示復數的虛部。

圖6：復數的實部和虛部

時域和頻域的每個分量都由包含了N個復數點的信號來描述。每個點都由用于描述信號分量的實部和虛部組成。有一個應用于現實生活中的電氣工程領域的實例：使用傅里葉變換可以幫助我們分析變化的電壓和電流。

圖7： 傅里葉變換中使用的實部和虛部展示

快速傅里葉變換（FFT）的過程是將一個包含N個樣本點的時域信號分解為N個時域信號，每個時域信號表示一個樣本點信息。第二步是計算這N個時域信號相對應的N個頻譜。最后，將N個頻譜合為一個頻譜。

點擊此處可以找到有關傅里葉變換的更多信息。

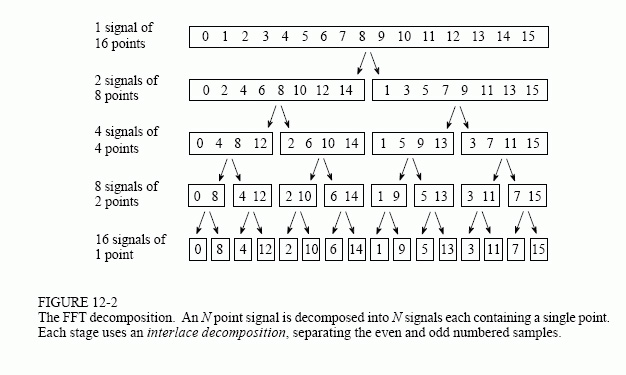
圖8：時域分解

使用傅里葉變換時的一些重要規則如下：

? 時域中的點數等于頻域中的點數。

? 假設您有一個包含DC值的正弦波 – 頻譜中的第一個點將具有零頻率值（DC值），而下一個點為正弦頻率。

? 當從時域轉為頻域時，可以使用第n個點的頻率進行繪制：f = (n-1) SR/N，其中N為樣本點數。

? 頻率為f = 1/T，其中T為周期。

讓我們來看一下下面的代碼，以了解在MATLAB中是如何實現傅里葉變換的。

t = 0:1/1000:1-1/1000;
x = sin(2*pi*30*t);
plot(t,x)

從向量t中可以觀察到，點采樣是在1/1000范圍內進行的，因此采樣率為1000 Hz（1000 1s或 s-1）。您還記得之前的文中提到的采樣率應該是信號頻率的兩倍嗎？

下面的正弦波的頻率為30Hz。

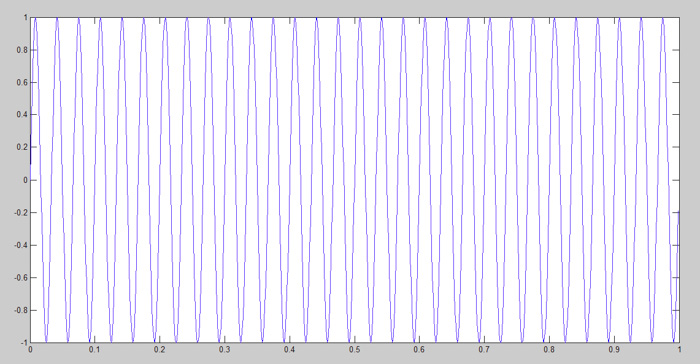
圖9：在MATLAB中生成的正弦波

當我們想要進行傅里葉變換時，使用fft(x)指令。

y = fft(x);
f = (0:length(y)-1)*1000/length(y);
plot(f,abs(y))

當我們在頻域中繪圖時，x軸將除以2。

使用傅里葉變換后，我們只需要一半的采樣率即可觀察到信號的頻譜分量。

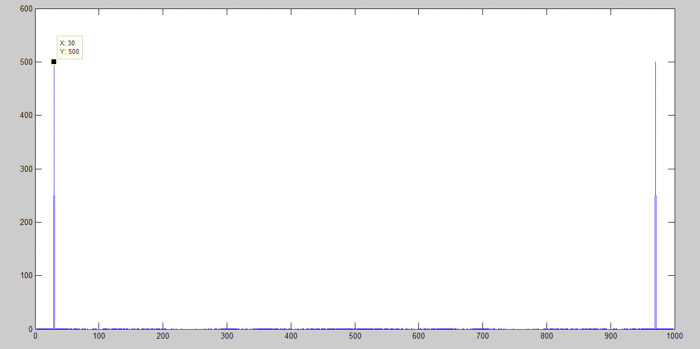
圖10：MATLAB中的fft函數圖

當在正弦信號上應用FFT時，其唯一的屬性是與時域中所描述的頻率點相對應的頻譜分量，在本例中為30 Hz。

如果將長度指令應用于向量t，則返回：

>> length(t)

ans =

1000

如圖 11所示，當我們對所有點進行繪制時，可以觀察到一個有趣的現象： 970 Hz(1000-30 Hz)處還有一個頻譜分量。這意味著y軸以500 Hz為中心發生了鏡像翻轉，對應了采樣率除以2的結果。

目前為止，我們的項目已經快要完成了。請繼續閱讀下一篇文章來了解如何添加失真濾波器使信號發生變形。然后，我們將在使用MATLAB創建的GUI上繼續對聲音信號進行處理。

審核編輯黃宇