MATLAB學(xué)習(xí)筆記之PID算法2
2.4.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //設(shè)置速度
float ActualSpeed ; //實(shí)際速度
float err ; //誤差
float err_last ; //最終誤差
float Kp , Kd , Ki ; //比例系數(shù)
float voltage ; //輸出電壓
float integral ; //積分值
float umax ; //積分上限
float umin ; //積分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( abs(pid.err)<= pid.umax )
{
index = 1 ;
pid.integral += pid.err ;
}
else
index = 0 ;
pid.voltage = pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*( pid.err-pid.err_last ) ;
pid.err_last = pid.err ;
pid.ActualSpeed = pid.voltage*1.0 ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<1000 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
printf( "%.2f\\n" , Speed ) ;
}
}
2.5 抗積分飽和型PID算法
2.5.1 實(shí)現(xiàn)原理
所謂積分飽和現(xiàn)象是指如果系統(tǒng)存在一個(gè)方向的偏差，PID控制器的輸出會(huì)因?yàn)榇嬖诜e分環(huán)節(jié)而不斷累積增大，從而導(dǎo)致執(zhí)行機(jī)構(gòu)達(dá)到極限位置，若控制器輸出響應(yīng)繼續(xù)增大，執(zhí)行器開(kāi)度不可能再增大，此時(shí)計(jì)算機(jī)輸出控制量超出了正常運(yùn)行范圍而進(jìn)入飽和區(qū)，一旦系統(tǒng)出現(xiàn)反向偏差，輸出響應(yīng)逐漸從飽和區(qū)退出，進(jìn)入飽和區(qū)時(shí)間越長(zhǎng)則退出飽和區(qū)的時(shí)間也就隨之增加，這段時(shí)間里，執(zhí)行機(jī)構(gòu)仍然停留在極限位置而不能隨著偏差方向立即作出相應(yīng)的改變，造成控制性能惡化，這種現(xiàn)象稱(chēng)為積分飽和現(xiàn)象或積分失控現(xiàn)象。實(shí)現(xiàn)抗積分飽和算法的基本思路是計(jì)算系統(tǒng)的響應(yīng)時(shí)，首先判斷上一時(shí)刻的控制量是否超出了極限范圍，如果超過(guò)上限，則只累計(jì)反向偏差，若低于下限，則只累計(jì)正向偏差，從而避免控制量長(zhǎng)時(shí)間停留在飽和區(qū)。
2.5.2 MATLAB算法
clc
clear
%PID初始化
len = 180 ; %運(yùn)算次數(shù)
y = zeros(1,len); %期望值
y_d = zeros(1,len); %過(guò)程值
err = zeros(1,len); %誤差值
err_0 = 0 ; %k時(shí)刻誤差
err_1 = 0 ; %k-1時(shí)刻誤差
y_d_last = 0 ; %k-1時(shí)刻輸出
integral = 0; %積分值
Kp = 0.2; %比例系數(shù)
Kd = 0.2; %微分值
Ki = 0.1 ; %積分值
max = 400 ; %積分上限
min = -200 ; %積分下限
index = 0 ; %積分有效性
%運(yùn)算過(guò)程
for k=1:1:len
y(k) = 200 ; %期望輸出
err_0 = y(k)-y_d_last; %計(jì)算偏差
if y_d_last>max
if abs(err_0) <= y(k)
index = 1 ;
if err_0 < 0
integral = integral+err_0; %誤差累計(jì)
end
else
index = 0 ;
end
elseif y_d_last<min
if abs(err_0) <= y(k)
index = 1 ;
if err_0 > 0
integral = integral+err_0; %誤差累計(jì)
end
else
index = 0 ;
end
else
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %誤差累計(jì)
else
index = 0 ;
end
end
y_d_last = Kp*err_0 + Ki*index*integral + Kd*(err_1-err_0); %位置型PID運(yùn)算公式
err_1 = err_0 ;
%更新參數(shù)
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%輸出圖像繪制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('輸出曲線(xiàn)');
xlabel('t')
ylabel('y(t)')
%誤差圖像繪制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('誤差曲線(xiàn)');
xlabel('t')
ylabel('e(t)')
MATLAB運(yùn)行結(jié)果如下圖所示。
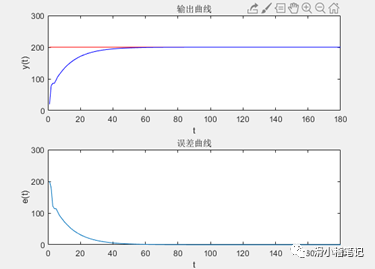
2.5.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //設(shè)置速度
float ActualSpeed ; //實(shí)際速度
float err ; //誤差
float err_last ; //最終誤差
float Kp , Kd , Ki ; //比例系數(shù)
float voltage ; //輸出電壓
float integral ; //積分值
float umax ; //積分上限
float umin ; //積分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( pid.ActualSpeed>pid.umax )
{
if( abs(pid.err)<=200 )
{
index = 1 ;
if( pid.err<0 )
pid.integral += pid.err ;
}
else
index = 0 ;
}
else if( pid.ActualSpeed
2.6 梯形積分PID算法
2.6.1 實(shí)現(xiàn)原理
根據(jù)梯形算法的積分環(huán)節(jié)公式
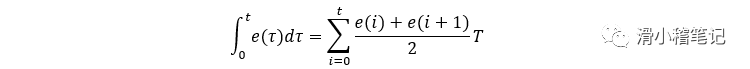
作為PID控制的積分項(xiàng)，其作用是消除余差，為了盡量減小余差，應(yīng)提高積分項(xiàng)運(yùn)算精度，為此可以將矩形積分改為梯形積分，具體實(shí)現(xiàn)的語(yǔ)句為pid.voltage = pid.Kppid.err+indexpid.Ki pid.integral/2+pid.Kd ( pid.err-pid.err_last ) ;
2.6.2 MATLAB算法
clc
clear
%PID初始化
len = 358 ; %運(yùn)算次數(shù)
y = zeros(1,len); %期望值
y_d = zeros(1,len); %過(guò)程值
err = zeros(1,len); %誤差值
err_0 = 0 ; %k時(shí)刻誤差
err_1 = 0 ; %k-1時(shí)刻誤差
y_d_last = 0 ; %k-1時(shí)刻輸出
integral = 0; %積分值
Kp = 0.2; %比例系數(shù)
Kd = 0.2; %微分值
Ki = 0.1 ; %積分值
max = 400 ; %積分上限
min = -200 ; %積分下限
index = 0 ; %積分有效性
%運(yùn)算過(guò)程
for k=1:1:len
y(k) = 200 ; %期望輸出
err_0 = y(k)-y_d_last; %計(jì)算偏差
if y_d_last>max
if abs(err_0) <= y(k)
index = 1 ;
if err_0 < 0
integral = integral+err_0; %誤差累計(jì)
end
else
index = 0 ;
end
elseif y_d_last<min
if abs(err_0) <= y(k)
index = 1 ;
if err_0 > 0
integral = integral+err_0; %誤差累計(jì)
end
else
index = 0 ;
end
else
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %誤差累計(jì)
else
index = 0 ;
end
end
y_d_last = Kp*err_0 + Ki*index*integral/2 + Kd*(err_1-err_0); %PID運(yùn)算公式
err_1 = err_0 ;
%更新參數(shù)
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%輸出圖像繪制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('輸出曲線(xiàn)');
xlabel('t')
ylabel('y(t)')
%誤差圖像繪制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('誤差曲線(xiàn)');
xlabel('t')
ylabel('e(t)')
2.6.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //設(shè)置速度
float ActualSpeed ; //實(shí)際速度
float err ; //誤差
float err_last ; //最終誤差
float Kp , Kd , Ki ; //比例系數(shù)
float voltage ; //輸出電壓
float integral ; //積分值
float umax ; //積分上限
float umin ; //積分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( pid.ActualSpeed>pid.umax )
{
if( abs(pid.err)<=200 )
{
index = 1 ;
if( pid.err<0 )
pid.integral += pid.err ;
}
else
index = 0 ;
}
else if( pid.ActualSpeed
聲明：本文內(nèi)容及配圖由入駐作者撰寫(xiě)或者入駐合作網(wǎng)站授權(quán)轉(zhuǎn)載。文章觀(guān)點(diǎn)僅代表作者本人，不代表電子發(fā)燒友網(wǎng)立場(chǎng)。文章及其配圖僅供工程師學(xué)習(xí)之用，如有內(nèi)容侵權(quán)或者其他違規(guī)問(wèn)題，請(qǐng)聯(lián)系本站處理。
舉報(bào)投訴
-
matlab
+關(guān)注
關(guān)注
188文章
2998瀏覽量
233260 -
直流電機(jī)
+關(guān)注
關(guān)注
36文章
1733瀏覽量
71415 -
PID
+關(guān)注
關(guān)注
37文章
1480瀏覽量
87380
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
熱點(diǎn)推薦
PID算法之模糊PID 精選資料推薦
這方面的需求而設(shè)計(jì)的。專(zhuān)家算法和模糊算法都?xì)w屬于智能算法的范疇，智能算法最大的優(yōu)點(diǎn)就是在控制模型未知的情況下，可以對(duì)模型進(jìn)行控制。這里需要注意的是，專(zhuān)家
發(fā)表于 07-19 06:29
使用C語(yǔ)言進(jìn)行PID算法實(shí)現(xiàn)
前文對(duì)PID算法離散化和增量式PID算法原理進(jìn)行來(lái)探索，之后又使用Matlab進(jìn)行了仿真實(shí)驗(yàn)，對(duì)PID
發(fā)表于 09-15 09:20
使用C語(yǔ)言進(jìn)行PID算法實(shí)現(xiàn)
前文對(duì)PID算法離散化和增量式PID算法原理進(jìn)行來(lái)探索，之后又使用Matlab進(jìn)行了仿真實(shí)驗(yàn)，對(duì)PID
發(fā)表于 09-16 09:11
PID算法學(xué)習(xí)筆記分享
最近在學(xué)習(xí)與無(wú)人機(jī)有關(guān)的一些控制算法，在這里做一些筆記，今天學(xué)的是有關(guān)于PID的算法。什么是PID
發(fā)表于 01-14 06:50
基于遺傳算法的PID 控制及其MATLAB 仿真
本 文介紹了遺傳算法和基于遺傳算法的PID 控制設(shè)計(jì)， 并對(duì)設(shè)計(jì)MATLAB/SIMULINK 下進(jìn)行了仿真，取得了良好的控制效果。關(guān)鍵詞：遺傳算法
發(fā)表于 06-11 09:06
?101次下載
OpenStack之Cinder學(xué)習(xí)筆記
OpenStack之Cinder學(xué)習(xí)筆記(開(kāi)關(guān)電源技術(shù)教程ppt)-該文檔為OpenStack之Cinder學(xué)習(xí)
發(fā)表于 09-23 12:40
?5次下載
PID算法學(xué)習(xí)筆記
最近在學(xué)習(xí)與無(wú)人機(jī)有關(guān)的一些控制算法，在這里做一些筆記，今天學(xué)的是有關(guān)于PID的算法。什么是PID
發(fā)表于 01-14 11:13
?9次下載
MATLAB學(xué)習(xí)筆記之PID算法3
為了消除系統(tǒng)的穩(wěn)態(tài)誤差，提高控制精度引入了積分環(huán)節(jié)，但是在啟動(dòng)，結(jié)束和大幅度增減設(shè)定時(shí)，短時(shí)間內(nèi)系統(tǒng)輸出有很大的偏差，會(huì)造成PID運(yùn)算的積分積累，導(dǎo)致控制量超過(guò)執(zhí)行機(jī)構(gòu)可能允許的最大動(dòng)作范囲所對(duì)應(yīng)
MATLAB如何實(shí)現(xiàn)PID？
實(shí)現(xiàn)PID控制：1.打開(kāi)MATLAB，啟動(dòng)MATLAB軟件。2.創(chuàng)建新的MATLAB腳本，在MATLAB
工商網(wǎng)監(jiān)
評(píng)論