1、拉普拉斯變換
(1)之前的一階電路和二階電路的分析,所應用的方法是根據(jù)電路定理和元件的電壓,電流關系建立線性常微分方程,通過求解微分方程的解求得電路的時域響應,這種方法又稱為經(jīng)典法。但是對于多個動態(tài)元件的復雜電路(一般指同時存在R,L,C的電路),直接求解微分方程比較麻煩,例如對于一個n階方程,直接求解時需要知道變量及其二階導數(shù)在t=0時刻的初值,但是這些值求解起來非常麻煩。所以對于高階系統(tǒng),一般采用積分變換法,將時域函數(shù)變?yōu)轭l域函數(shù),從而將時域微分方程轉(zhuǎn)為頻域代數(shù)方程求解,求出頻域解后在還原為時域解。拉普拉斯變換是一種重要的積分變換。

2、拉普拉斯變換的性質(zhì)


3、典型信號的拉普拉斯變換
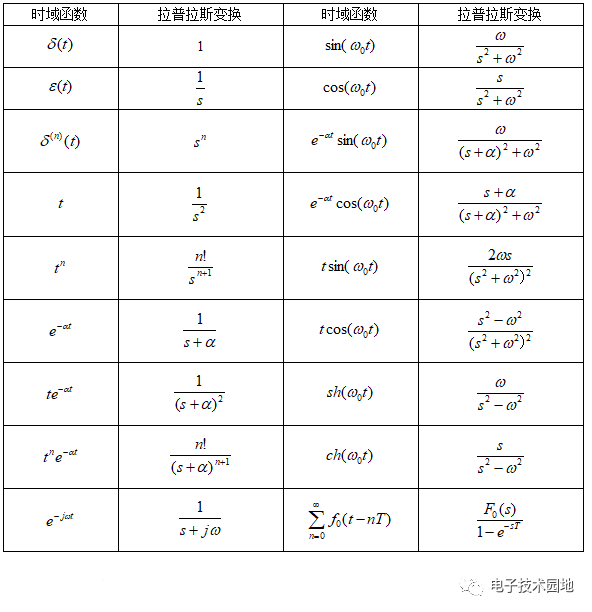
(1)拉普拉斯變換和傅里葉變換一樣,都應盡量避免積分運算,利用性質(zhì)和基本信號的公式來求解。
(2)關于周期信號的拉氏變換有

4、拉普拉斯變換在電路中的應用
(1)利用拉普拉斯變換來分析電路的參數(shù)過程如下:
第一步:將輸入激勵進行拉氏變換;
第二步:將電路中的R,L,C元件的拉氏變換形式寫出來,列寫所求的變量與激勵之間的關系;
第三步:反解復頻域形式的變量;
第四步:將復頻域形式的變量做拉氏反變換。
(2)元件的時域與復頻域形式的電壓電流關系(電壓電流均取關聯(lián)參考方向)
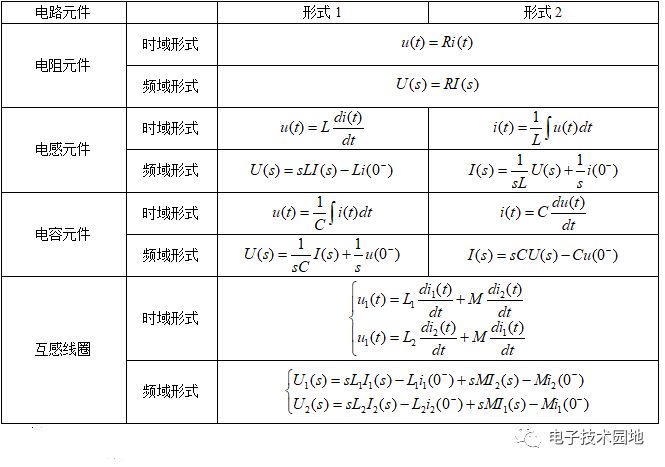
5、例題分析
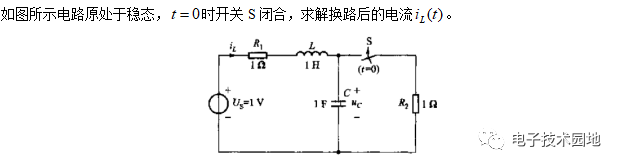

-
函數(shù)
+關注
關注
3文章
4371瀏覽量
64209 -
頻域
+關注
關注
1文章
90瀏覽量
26541 -
微分方程
+關注
關注
0文章
21瀏覽量
9639
發(fā)布評論請先 登錄
計算機Fortran編程實現(xiàn)偏微分方程拉普拉斯變換
拉普拉斯變換的基本定理
拉普拉斯變換及其逆變換表拉普拉斯變換及其逆變換表






 拉普拉斯變換在電路中的應用
拉普拉斯變換在電路中的應用
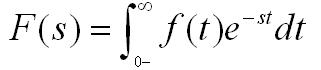










評論