時(shí)域和頻域
對(duì)時(shí)域和頻域最直觀的感受可以從波形上看出來(lái)。下圖<1>是一個(gè)1MHz的方波時(shí)域波形,下圖<2>是此方波的頻域波形。時(shí)域圖的橫軸坐標(biāo)是時(shí)間(us),縱軸坐標(biāo)是信號(hào)電壓幅度(V)。頻域圖的橫軸坐標(biāo)是頻率(xHz),縱軸坐標(biāo)是信號(hào)幅度(dB)。它們是使用LTspice仿真軟件得到。
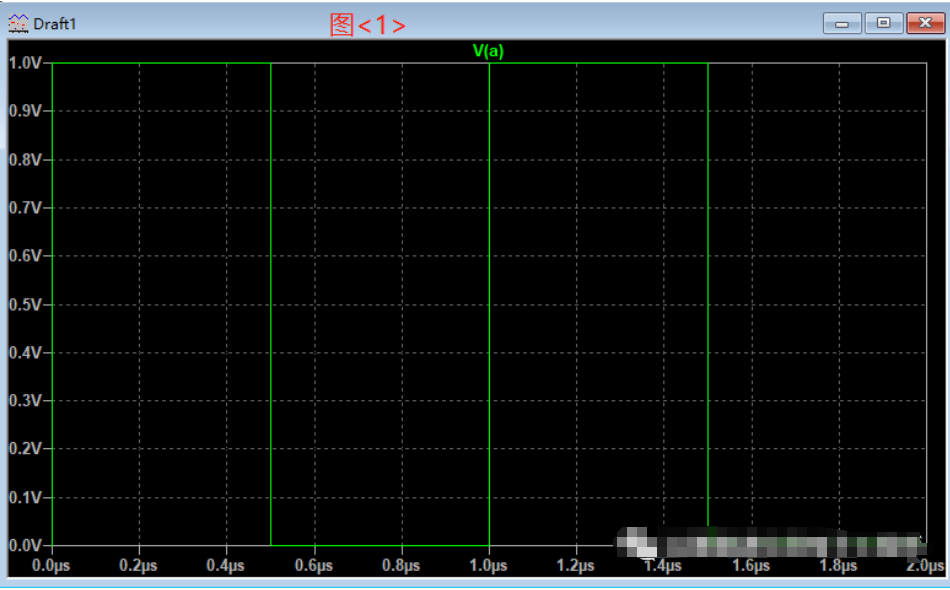
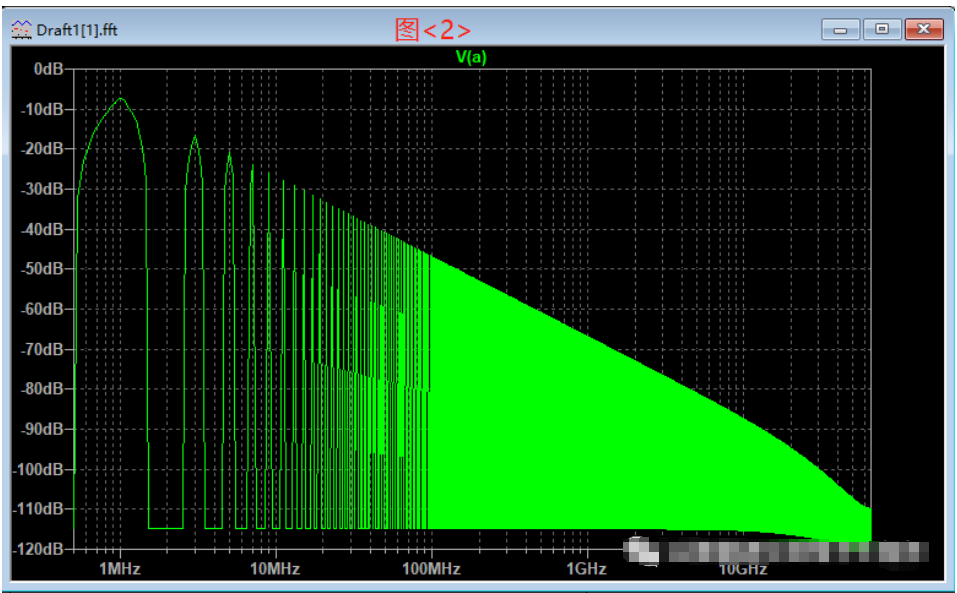
時(shí)域就像我們的人生,從出生開始向前延伸,沒(méi)有機(jī)會(huì)重來(lái)。信號(hào)在時(shí)域中也是一直向前,從波形上看就是沿著時(shí)間軸,顯示每時(shí)每刻信號(hào)的電壓和電流的樣子,它是以時(shí)間為基準(zhǔn)的。頻域在我們真實(shí)世界中是不存在的,它是以信號(hào)的頻率為基準(zhǔn),顯示信號(hào)包含的各個(gè)頻率點(diǎn)對(duì)應(yīng)的電壓和電流的樣子。時(shí)域的信號(hào)經(jīng)過(guò)數(shù)學(xué)計(jì)算得到的就是頻域信號(hào),有三種方法實(shí)現(xiàn)信號(hào)從時(shí)域到頻域的轉(zhuǎn)變(傅里葉積分、離散傅里葉變換和快速傅里葉變化)。
任何波形都是正弦波的集合
在頻域中唯一存在的波形就是正弦波。換句話說(shuō)時(shí)域中的任何波形都是由頻域中的一系列正弦波組合而成。這些正弦波分量都有各自相關(guān)的頻率、幅度和相位。把所有這些頻率值和幅度值的集合稱為波形的頻譜。頻譜中的正弦波頻率是時(shí)域中信號(hào)頻率的整數(shù)倍。第一個(gè)正弦波頻率稱為一次諧波,第二個(gè)正弦波分量稱為二次諧波,依次類推。而零次諧波就是直流分量值。
例如上圖<2>,假設(shè)此理想方波的幅度是1V。它的所有偶次諧波幅度都為0,只存在奇次諧波。奇次諧波的幅度為
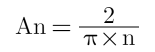
An: n次諧波的幅度
n:諧波數(shù)
要想從頻譜信號(hào)中得到它的時(shí)域波形,只需要將頻域中所有頻率的信號(hào)轉(zhuǎn)換成時(shí)域中正弦波的集合,并且將這些正弦波全部疊加即可。圖3是包含10諧波的方波,圖4是包含100次諧波的方波。可以看出包含的諧波分量越多,方波上升沿和下降沿越陡峭,方波越完整。
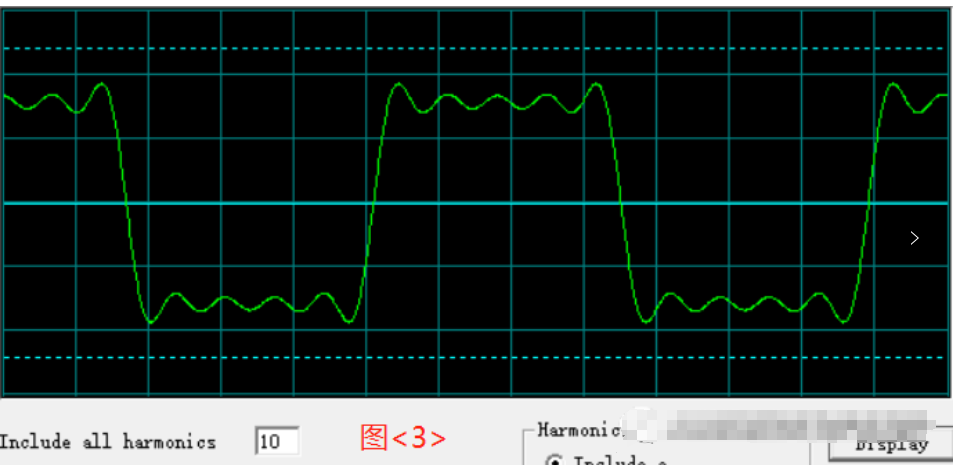
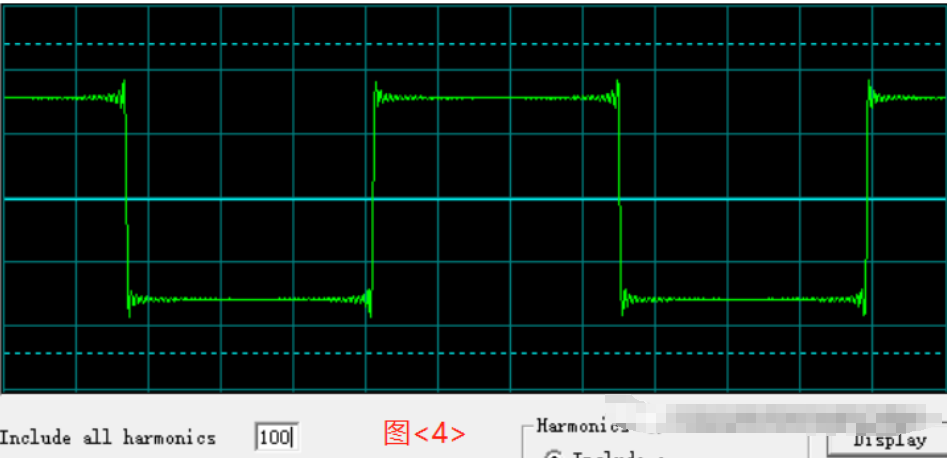
問(wèn)題來(lái)了,一個(gè)波形包含多少諧波分量就足夠了?是10次、100次、還是越多越好?這就引入了帶寬的概念。
帶寬
所謂帶寬是指從一個(gè)信號(hào)的頻域角度看,為了充分表現(xiàn)時(shí)域波形的特征,在其頻譜中需要包含的頻率范圍,即有效頻率范圍。在此范圍之外的頻率分量可以不用考慮。
通常所謂有效是指,實(shí)際信號(hào)的諧波幅度高于相同頻率的理想方波中相應(yīng)諧波幅度70%的頻率點(diǎn)。高于此點(diǎn)的諧波幅度會(huì)很低,對(duì)恢復(fù)信號(hào)時(shí)域波形已經(jīng)沒(méi)有多少貢獻(xiàn),可以忽略。
有一個(gè)關(guān)于信號(hào)上升時(shí)間和帶寬的經(jīng)驗(yàn)法則是:
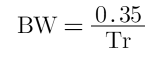
BW是信號(hào)帶寬
Tr是信號(hào)的上升時(shí)間
結(jié)合前一篇文章提到的大多數(shù)信號(hào)的上升時(shí)間是其周期的十分之一,可以粗濾估算信號(hào)帶寬。
有一種情況是:如果實(shí)際電路的阻抗控制不好,導(dǎo)致信號(hào)發(fā)生振鈴等現(xiàn)象,此時(shí)這個(gè)信號(hào)的帶寬會(huì)比沒(méi)有振鈴現(xiàn)象的信號(hào)帶寬要大。在頻譜上會(huì)看到,振鈴頻率點(diǎn)對(duì)應(yīng)的頻譜頻率處會(huì)有尖峰幅值出現(xiàn)。因此當(dāng)在EMC實(shí)驗(yàn)中出現(xiàn)某些頻率點(diǎn)超標(biāo),而整個(gè)電路中又沒(méi)有對(duì)應(yīng)頻率的信號(hào)時(shí),檢查數(shù)字信號(hào)是否有振鈴,也是一個(gè)方向。因?yàn)殡娐分械恼疋徔赡軙?huì)使高頻分量的幅度增加,進(jìn)而導(dǎo)致輻射幅度增加。
第二種情況是:同樣頻率的正弦波和方波帶寬也不相同。方波的帶寬更大,這是因?yàn)樾盘?hào)帶寬是由信號(hào)上升時(shí)間決定,而不是由頻率決定。上升時(shí)間越短,信號(hào)包含的高頻諧波越多,信號(hào)帶寬越寬,EMI噪聲越大。
在EMI對(duì)策中,有個(gè)粗陋的經(jīng)驗(yàn)值(僅僅是經(jīng)驗(yàn)值),數(shù)字信號(hào)的濾波電路截止頻率要保證25~35次以內(nèi)的諧波都要存在,以外的諧波濾除。
-
仿真
+關(guān)注
關(guān)注
51文章
4247瀏覽量
135405 -
信號(hào)完整性
+關(guān)注
關(guān)注
68文章
1438瀏覽量
96502 -
時(shí)域
+關(guān)注
關(guān)注
1文章
73瀏覽量
28861 -
頻域
+關(guān)注
關(guān)注
1文章
90瀏覽量
26561 -
LTspice
+關(guān)注
關(guān)注
1文章
126瀏覽量
13877
發(fā)布評(píng)論請(qǐng)先 登錄
于博士《信號(hào)完整性--系統(tǒng)化設(shè)計(jì)方法及案例分析》高級(jí)研修班
我們?yōu)槭裁粗匾曄到y(tǒng)化信號(hào)完整性設(shè)計(jì)方法(于博士信號(hào)完整性)
信號(hào)完整性為什么寫電源完整性?
何為信號(hào)完整性?信號(hào)完整性包含哪些
什么是信號(hào)完整性

信號(hào)完整性與電源完整性仿真分析

信號(hào)完整性分析基礎(chǔ)知識(shí)
關(guān)于信號(hào)完整性的31個(gè)知識(shí)點(diǎn)匯總
信號(hào)完整性中需要掌握的基礎(chǔ)知識(shí)點(diǎn)資料下載

信號(hào)完整性與電源完整性的仿真

高速電路設(shè)計(jì)常見的知識(shí)點(diǎn)
把信號(hào)完整性設(shè)計(jì)落到實(shí)處






 信號(hào)完整性的知識(shí)點(diǎn)
信號(hào)完整性的知識(shí)點(diǎn)











評(píng)論