以21700鋰離子電池組為研究對象,對不同排布方式下的鋰電池分別控制電池間距?對流換熱系數和相變材料(PCM)導熱率,并對其進行有限元仿真?研究了電池間距?對流換熱系數和PCM導熱率對相變電池熱管理系統(BTMS)下不同排布方式(長方形?四邊形?六邊形)的電池組溫度場的影響?結果表明:當電池間距為4mm和6mm時,3者具有近似的最高溫度,而當電池間距為2mm和1mm時,長方形排布的電池組最高溫度最大,在2mm時長方形排布的電池組最大溫升分別為四邊形排布下和六邊形排布下的電池組的105.86%和108.25%,而3者的溫差均隨間距增大,總體呈現出變小的趨勢;在不同的對流換熱系數下,長方形排布的電池組最高溫度總是最大而四邊形最小,隨著對流換熱系數的增大,3者溫差呈現出變大的趨勢;隨著PCM導熱系數的增大,3者的最高溫度均不斷下降且下降速率越來越小,在5種不同PCM導熱系數下,長方形排布的電池組最大溫升平均是四邊形排布和六邊形排布電池組的105.31%和106.02%,3者的潛熱儲熱階段的溫差均有減小,顯熱階段對長方形和六邊形的溫差沒有影響,四邊形的溫差卻不斷增大?綜合考慮最高溫度和溫差,采用六邊形排布的鋰電池組在PCM熱管理下的熱性能最佳?

作者：郭茶秀 魏金宇

鄭州大學 機械與動力工程學院,河南鄭州

鋰離子電池作為一種具有高能量密度且循環壽命長的電化學儲能系統,已經在電動汽車市場中有了廣泛的應用?然而,鋰離子電池在各種條件下的熱問題研究和電池熱管理系統并沒有得到充分的解決?因此,對于基于鋰離子的電動汽車,需要一種有效的電池熱管理系統(batterythermalmanagementsystem,BTMS)來快速散去電池組內部產生的熱量?空氣冷卻作為最傳統的冷卻方式 ^[1-5]^ ,由于空氣本身較低的導熱率,很難滿足電池在高功率放電時的散熱需求;液冷是如今BTMS應用最廣泛的冷卻方式 ^[6-8]^ ,具有散熱效果好?速度快等優點?但其一般都有著較為復雜的結構和較高的價格,而且對密封性要求較高,一般在極端情況下使用?Hal-laj等 ^[9]^ 首先提出了將相變材料用于BTMS的想法?Sabbah等 ^[10]^ 研究了在不同放電速率和環境溫度下PCM(phasechangematerial)和空氣熱管理系統的性能,結果表明,在高放電倍率和高溫環境下,空氣冷卻需要大量的功耗才能達到PCM熱管理系統的效果?在研究PCM散熱的過程中研究人員發現,當電池溫度沒有超過PCM熔點時,其對電池的最高溫度和溫差的升高有著很好的抑制作用?

前人對于PCM散熱和電池的排布優化已經進行了相關的研究,張曉光等 ^[11]^ 對電池間距的均勻排布和不均勻排布情況進行了研究,在相同體積的相變材料中對電池間距進行非均勻排布,最優排布的最大溫差比優化前降低了34%?以上對電池排布的研究,都選擇了間距為變量,采用均勻間距或非均勻間距,但都沒有對排布方式進行研究,因此作者選擇排布方式為變量,研究了電池間距?對流換熱系數和PCM導熱率對相變BTMS下不同排布方式的電池組溫度場的影響?

本文以21700鋰離子電池組為研究對象,通過對不同排布方式下的鋰電池分別控制電池間距?對流換熱系數和PCM導熱率,并分別進行仿真分析,研究電池間距?對流換熱系數和PCM導熱率的變化對不同排布方式下以相同比體積的相變材料包裹下21700鋰離子電池的最高溫度和溫差的影響?

01數值方法

幾何模型

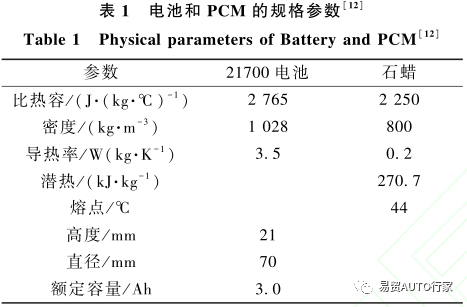
采用模擬軟件 AnsysFluent19.2,以 21700 型圓柱形鋰離子電池為研究對象,以數值模擬的方法模擬了使用 PCM( 石蠟) 熱管理系統下的鋰電池不同排布方式的傳熱過程。為了研究不同排布方式對 PCM 熱管理系統的影響,設計了以長方形、四邊形和六邊形排布的 3 種電池組,以相同比體積 ( 相變材料體積與電池個數比值)的相變材料包裹電池。鋰電池和相變材料物性參數如表 1 所示。

電池產熱模型

在進行數值分析前,要先得到電池的產熱功率,通常用Bernardi等 ^[13]^ 提出的產熱公式得到與實驗中的實際結果較為符合的產熱功率,所以本文中使用Bernardi產熱公式來計算電池的產熱功率:

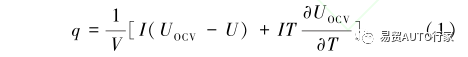
式中:q為電池的產熱功率,W/m3;I為電池工作時的電流,A;V為電池的體積,m3;T為電池的初始熱力學溫度,K;UOCV為電池的開路電壓,V;U為電池的端電壓,V;?UOCV?T為電池的熵系數,mV/K?

Chen等 ^[12]^ 實驗得到了21700型鋰電池在35℃下以4C倍率放電時的開路電壓?端電壓和熵系數,如圖1所示?結合表1的電池參數在擬合后,可以得到4C倍率放電情況下的電池產熱功率-時間關系式:

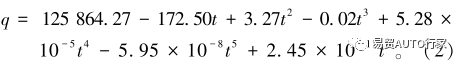
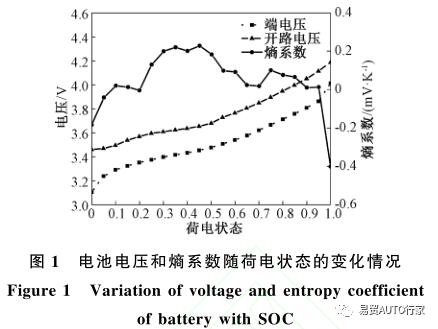
產熱模型驗證

為了驗證產熱公式的可靠性,使用Fluent19.2對單個電池在自然對流下以4C倍率放電的產熱情況進行模擬并與實驗情況進行對比?環境溫度設置為35℃,自然對流系數為10W/(m2·K),結果如圖2所示?

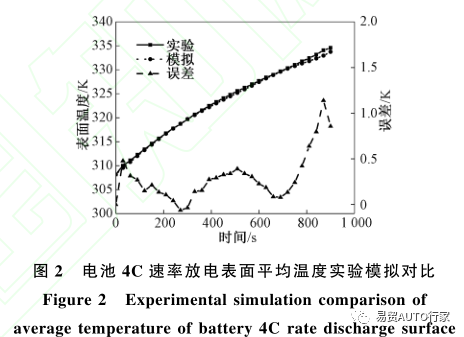
由圖2中數據可以看出,實驗和模擬中電池的溫升都是先快后慢,總體趨勢相同,且最大誤差僅為1.14K,實驗與模擬結果誤差不超過5%,由此可以看出,產熱公式具有較高的精確性和可靠性,可以滿足計算模擬的需求?

網格無關性驗證

為了減少網格數量對實驗結果產生的影響并且節省計算時間,需要選取合適大小的網格進行計算?圖3為網格無關性驗證?

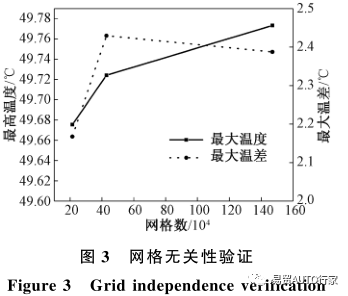
從圖3可以看出,當網格數從214344增加到428016時,最高溫度和最大溫差都變化較大,而繼續增大網格數則變化不大?所以,為了有效利用計算資源并保證模擬的精確性,本文的模擬采用網格數為428016的網格模型進行計算?

控制方程

為了簡化計算過程,首先要對傳熱過程做出以下假設?

①電池內部物性參數和產熱是均勻的;②PCM熱物性參數各向同性,且不隨溫度變化;③PCM內部只考慮熱傳導,忽略液態PCM的熱對流;④不考慮傳熱過程中的輻射?

模擬時電池和PCM的初始溫度和環境溫度都為35℃,空氣自然對流系數為10W/(m2·K)?電池內部傳熱方程:

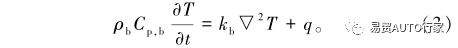
相變材料內部傳熱方程:

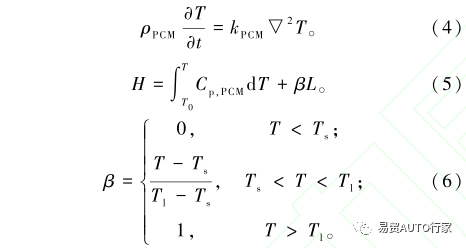
電池與 PCM 接觸面的邊界條件:

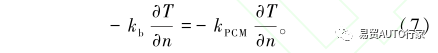
外表面邊界條件:

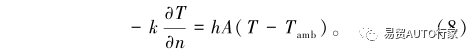
式中:ρb為電池的密度,kg/m3;Cp,b為電池的比熱容,J/(kg·K);kb為電池的導熱率,W/(m·K);?T?t為溫度梯度;q為體熱源,W;ρPCM為PCM的密度kg/m3;Cp,PCM為電池的比熱容,J/(kg·K);kPCM為電池的導熱率W/(m·K);β為PCM的液相分數;L為PCM的潛熱,kJ/kg;Ts和Tl分別為相變開始和終止的溫度,K;h為自然對流系數,取10W/(m2·K);Tamb為環境溫度,取35℃?

02結果與討論

排布方式對電池溫度場分布的影響

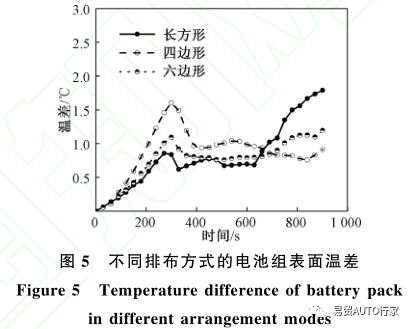
圖4和圖5顯示了電池在4C速率放電情況下,不同排布方式的電池組表面最高溫度和溫差隨時間的變化情況?

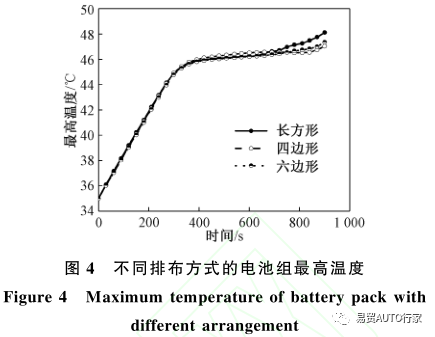
由圖4可以看出,在達到PCM的熔點前,3種排布方式的電池組的最高表面溫度均以較快的速率上升,在達到熔點后則上升速率迅速放緩,直至600s時,長方形排布的電池組上升速率開始增大并很快超過四邊形排布和六邊形排布的電池組,放電結束時長方形排布?四邊形排布和六邊形排布的電池組表面最高溫度分別為48.12℃?47.03℃和47.35℃?

由圖5中可看出,在300s前,電池組表面溫差在3種排布方式下均以一定的速率上升,而在達到峰值后均出現了一定程度的下降?在300~600s時,3種排布方式下溫差均保持穩定,而600s后,長方形排布的電池組溫差開始上升,而四邊形排布和六邊形排布的電池組溫差依然保持穩定?3種排布下最大溫差分別為1.79℃(長方形),1.60℃(四邊形)和1.19℃(六邊形)?

電池間距對電池溫度場分布的影響

將電池以1?2?4和6mm的間距排布,長方形和四邊形排布下電池數量為20個,六邊形排布下為19個,所以六邊形排布總體積為長方形和四邊形排布的19/20,以相同的比體積計算得到不同排布方式等效的間距(2d),如表2所示,3種排布方式的電池組俯視圖如圖 6 所示。

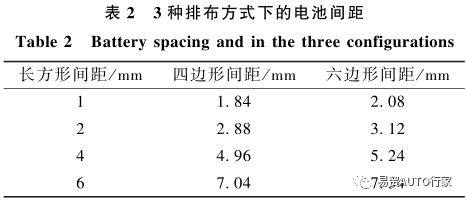
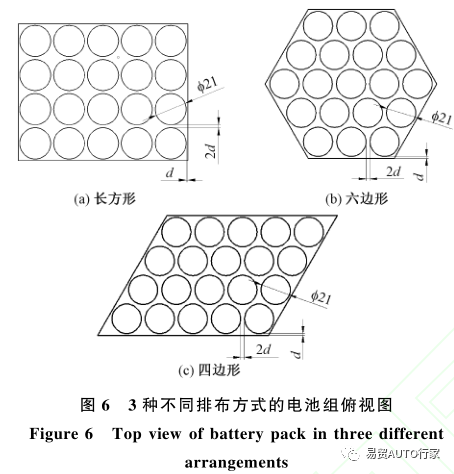
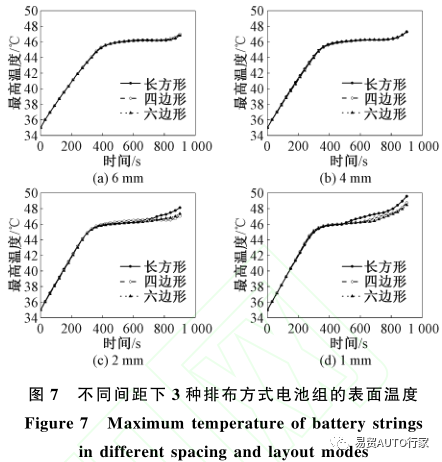
圖7為不同間距下3種排布方式電池組的表面最高溫度隨時間的變化情況?從圖7中可以看出,隨著電池間距的不斷減小,在放電結束時的最高溫度不斷增大,以長方形排布下的電池組為例,在1?2?4和6mm的間距下,在放電結束時的最高溫度分別為49.6?48.4?47.3和46.8℃,且在PCM顯熱儲熱階段的最高溫度上升速度也不斷增大?同樣以長方形排布為例,在1?2?4和6mm的間距下,表面最高溫度達到PCM熔點的時間分別為261?266?293和328s?同時也可以看出,不同排布方式下不斷減小間距,最高溫度的變化幅度也有所不同,在4?6mm的間距下,3種排布方式下的最高溫度變化趨勢基本相同,而在1?2mm的間距下,長方形排布下電池組的最高溫度在放電后期的上升幅度要大于四邊形排布和六邊形排布的電池組,所以也導致在小間距放電結束時,長方形排布下電池組的最高溫度要大于四邊形排布和六邊形排布,例如在1mm的間距下放電結束時3種排布方式的最高溫度分別為49.6℃(長方形)?48.8℃(四邊形)和48.5℃(六邊形)?

圖8為不同間距下3種排布方式下電池組的表面溫差隨時間的變化情況?

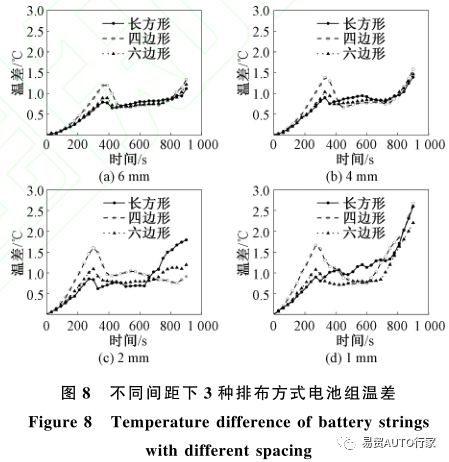
從圖8可以看出,在不同間距下,3種排布的電池表面溫差在300s前都在不斷上升,而四邊形排布下的電池組溫差上升速率總是要大于其他2種排布方式,在300~600s時,3種排布方式下溫差均保持穩定,在600s之后3種排布方式下的溫差則又開始上升且隨著間距的減少上升速率不斷增大?這也導致隨著間距的減少,3種排布方式下的溫差均不斷增大?以四邊形排布為例,在1?2?4和6mm的間距下的最大溫差分別為2.67?1.60?1.57和1.33℃?

對流換熱系數對電池溫度場分布的影響

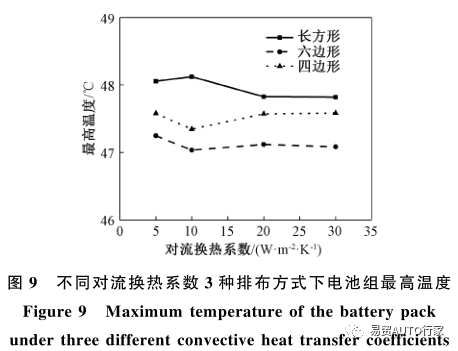
圖9為不同對流換熱系數下3種排布方式電池組的表面最大溫度隨時間的變化情況?從圖9可以看出,長方形排布電池組的最高溫度總是最大而六邊形排布的電池組總是最小,隨著對流換熱系數的變化,3種排布方式下的最高溫度并無顯著變化?圖10為不同對流換熱系數下3種排布方式電池組的表面溫差隨時間的變化情況?

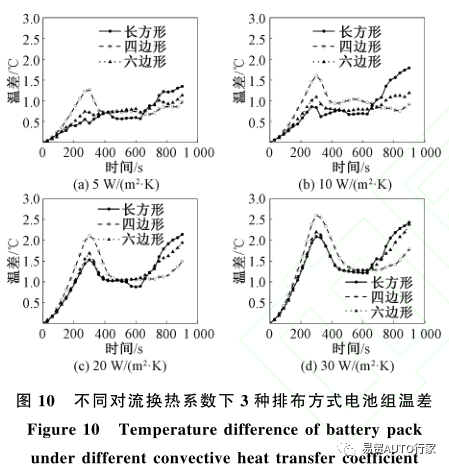
從圖10可以看出,隨著對流換熱系數的增大,在300s前和600s后,溫差的上升速率有著明顯的上升,其中四邊形排布的電池組在300s前上升速率最大而在600s后最小,長方形排布的電池組則與之相反,300s前上升速率最小而在600s后最大,而六邊形排布的電池組相較于其他兩種排布方式溫差波動較小,最大溫差也最小?以20W/(m2·K)為例,3種排布方式的最大溫差分別為2.14℃(長方形)?2.11℃(四邊形)和1.94℃(六邊形)?

相變材料導熱系數對電池溫度場分布的影響

相變材料的導熱系數對于PCM熱管理系統的性能有著很大的影響,為了研究PCM導熱系數對不同排布方式下電池溫度場的影響,在模擬中使用導熱系數不同其他物性相同的PCM進行計算?

圖11為不同導熱系數下3種排布方式電池組的表面最大溫度隨時間的變化情況?3種排布方式下的電池組最大溫度有著相同的變化趨勢,隨著導熱系數的不斷增大,最高溫度不斷減小,且減小的速率隨著導熱系數的增大不斷減小?在3種排布方式中,長方形排布的電池組最高溫度總是比其他排布方式要高0.5℃左右,而四邊形排布和六邊形排布電池組的最高溫度差距較小,當導熱系數小于1W/(m·K)時,六邊形的最高溫度大于四邊形,當導熱系數大于1W/(m·K)時,四邊形的最高溫度大于六邊形?

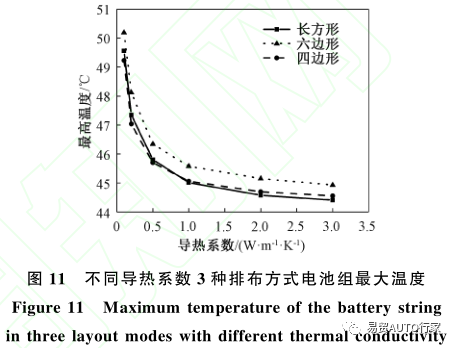
圖 12 為不同導熱系數下 3 種排布方式電池組的表面溫差隨時間的變化情況?？梢钥闯鲭S著導熱系數的增大,長方形排布和六邊形排布下的電池組

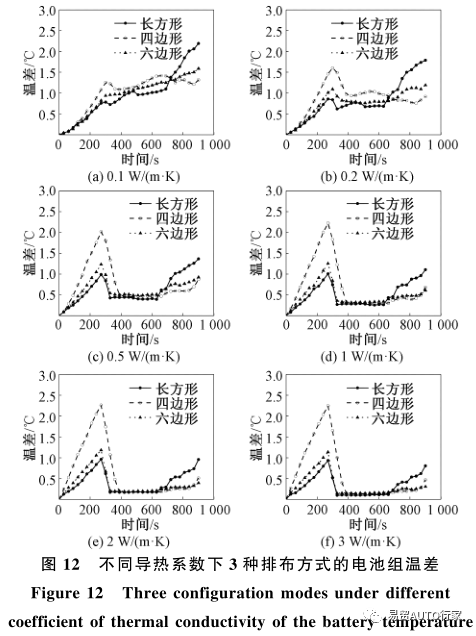
溫差在300s前趨勢基本沒有變化,而在300s后的溫差有著明顯減小;四邊形排布下的電池組在300s前溫差隨著導熱系數的增大不斷增大,直至導熱系數達到1W/(m·K)時,溫差不再上升變化趨勢保持不變,在300s后溫差有著明顯減小?在導熱系數大于0.1W/(m·K)時,四邊形排布下的電池溫差在300s前要明顯大于其他2種排布方式,而長方形排布下的電池組溫差在600s后要明顯大于其他2種排布方式?

03結論

本文以21700鋰電池組為研究對象,通過數值模擬的方法研究了電池間距,對流換熱系數和PCM導熱系數對PCM熱管理系統下不同排布方式電池組的溫度場影響,得到以下結論:

(1)電池間距大于4mm時,3種排布方式下的電池組最大溫度和溫差基本相同;小于4mm時,長方形排布的電池組的最高溫度最大,六邊形排布的電池組最大溫差最小,說明排布方式在相變材料不足量時對電池組溫度場影響較大?

(2)在不同對流換熱系數下,長方形排布的電池組最高溫度均為最大,四邊形排布均為最小;六邊形排布的電池組最大溫差均為最小,且隨著對流換熱系數的增大,最大溫差均不斷增大,這是由于不同排布方式的熱管理系統內部不同位置換熱條件不同,而對流換熱系數的增大也增大了這一差異?

(3)隨著PCM導熱系數的增大,3種排布下電池組最高溫度均不斷減小,長方形排布的電池組最高溫度總是最大;3種排布方式的溫差在300s后溫差均不斷減小,在300s前長方形排布和六邊形排布的電池組溫差無顯著變化而四邊形排布的電池組溫差上升速度則顯著增大,直至導熱系數達到1W/(m·K)時,溫差不再上升變化趨勢保持不變?

(4)綜合考慮最高溫度和溫差,采用六邊形排布的鋰電池組在PCM熱管理下的熱性能最佳?

審核編輯：湯梓紅