1、簡(jiǎn)介
量化是優(yōu)化神經(jīng)網(wǎng)絡(luò)以實(shí)現(xiàn)高效推理和設(shè)備執(zhí)行同時(shí)保持高精度的最成功方法之一。通過(guò)將常規(guī)32位浮點(diǎn)格式的權(quán)重和激活壓縮為更高效的低位定點(diǎn)表示,如INT8,這樣可以在邊緣設(shè)備上部署神經(jīng)網(wǎng)絡(luò)時(shí)降低功耗并加速推理。
盡管量化具有明顯的功率和延遲優(yōu)勢(shì),但由于精度降低,量化是以增加噪聲為代價(jià)的。然而,近年來(lái)的研究人員已經(jīng)表明,神經(jīng)網(wǎng)絡(luò)對(duì)這種噪聲是魯棒的,并且可以使用訓(xùn)練后量化技術(shù)(PTQ)以最小的精度下降量化到8比特。
PTQ可能非常有效,通常只需要訪問(wèn)一個(gè)小的校準(zhǔn)數(shù)據(jù)集,但當(dāng)應(yīng)用于神經(jīng)網(wǎng)絡(luò)的低位量化(≤4位)時(shí)會(huì)受到影響。同時(shí),量化感知訓(xùn)練(QAT)已成為事實(shí)上的標(biāo)準(zhǔn)方法,用于實(shí)現(xiàn)低比特量化,同時(shí)保持接近全精度的精度。通過(guò)模擬訓(xùn)練或微調(diào)期間的量化操作,網(wǎng)絡(luò)可以適應(yīng)量化噪聲,并達(dá)到比PTQ更好的解決方案。
本文重點(diǎn)關(guān)注量化權(quán)重在量化感知訓(xùn)練過(guò)程中發(fā)生的振蕩。在量化神經(jīng)網(wǎng)絡(luò)的優(yōu)化中,這是一個(gè)鮮為人知且研究不足的現(xiàn)象,在訓(xùn)練期間和訓(xùn)練后對(duì)網(wǎng)絡(luò)產(chǎn)生了重大影響。當(dāng)使用流行的直通估計(jì)器(STE)進(jìn)行QAT時(shí),權(quán)重似乎在相鄰量化級(jí)別之間隨機(jī)振蕩,從而在優(yōu)化過(guò)程中導(dǎo)致有害噪聲。有了這一見解,作者調(diào)研了QAT的最新進(jìn)展,這些進(jìn)展聲稱性能得到了改善,并評(píng)估了它們?cè)诮鉀Q這種振蕩行為方面的有效性。
權(quán)重振蕩的一個(gè)不利癥狀是,它們會(huì)破壞在訓(xùn)練期間收集的批量歸一化層的估計(jì)推斷統(tǒng)計(jì)數(shù)據(jù),導(dǎo)致驗(yàn)證準(zhǔn)確性差。作者發(fā)現(xiàn)這種效應(yīng)在具有深度可分離層的高效網(wǎng)絡(luò)(如MobileNets或EfficientNets)的低位量化中尤為明顯,但可以通過(guò)在訓(xùn)練后重新估計(jì)批量歸一化統(tǒng)計(jì)數(shù)據(jù)來(lái)有效解決。
雖然批量歸一化重新估計(jì)克服了振蕩的一個(gè)顯著癥狀,但它并沒(méi)有解決其根本原因。為此,我們提出了兩種有效減少振蕩的新算法:振蕩抑制和迭代權(quán)重凍結(jié)。通過(guò)在振蕩源處處理振蕩,本文的方法提高了精度,超出了批量歸一化重新估計(jì)的水平。本文表明,這兩種方法在高效網(wǎng)絡(luò)的4-bit和3-bit量化方面都取得了最先進(jìn)的結(jié)果,如MobileNetV2、MobileNetV3和ImageNet上的EfficientNet lite。
2、QAT中的振蕩
首先研究了為什么權(quán)值在量化感知訓(xùn)練中會(huì)振蕩,以及這種現(xiàn)象如何在實(shí)踐中影響神經(jīng)網(wǎng)絡(luò)訓(xùn)練。
2.1、量化感知訓(xùn)練

2.2、振蕩問(wèn)題

在附錄A.3中表明降低學(xué)習(xí)率會(huì)降低振蕩的振幅,但不會(huì)影響其頻率。
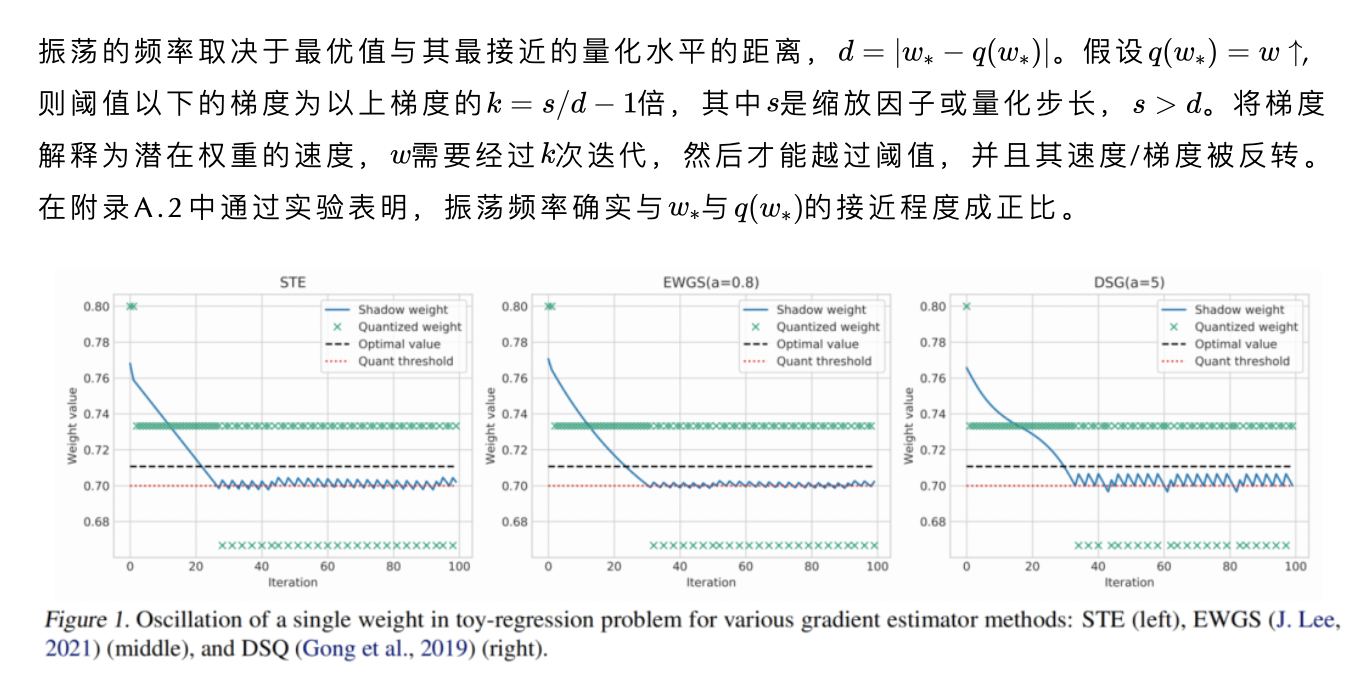
值得注意的是,這種行為與隨機(jī)舍入有相似之處,其中潛在權(quán)重與量化水平的接近程度與舍入到該水平的概率有關(guān)。然而,在STE中,隨機(jī)性的來(lái)源于梯度的離散性質(zhì),而不是采樣。可以注意到,振蕩并不是標(biāo)準(zhǔn)STE獨(dú)有的,而是存在于文獻(xiàn)中提出的STE的幾種變體中,在圖1中給出了其中的一小部分。
2.3、實(shí)踐中的振蕩
這些振蕩不僅僅是這個(gè)toy例子的副作用。它們確實(shí)存在于更大的神經(jīng)網(wǎng)絡(luò)中,對(duì)它們的優(yōu)化具有重要意義。圖2顯示了使用ImageNet上的LSQ訓(xùn)練的MobileNetV2的深度可分離層中接近收斂的3位量化權(quán)重的進(jìn)展。可以觀察到,許多權(quán)重似乎在2個(gè)相鄰的量化級(jí)別之間隨機(jī)振蕩。
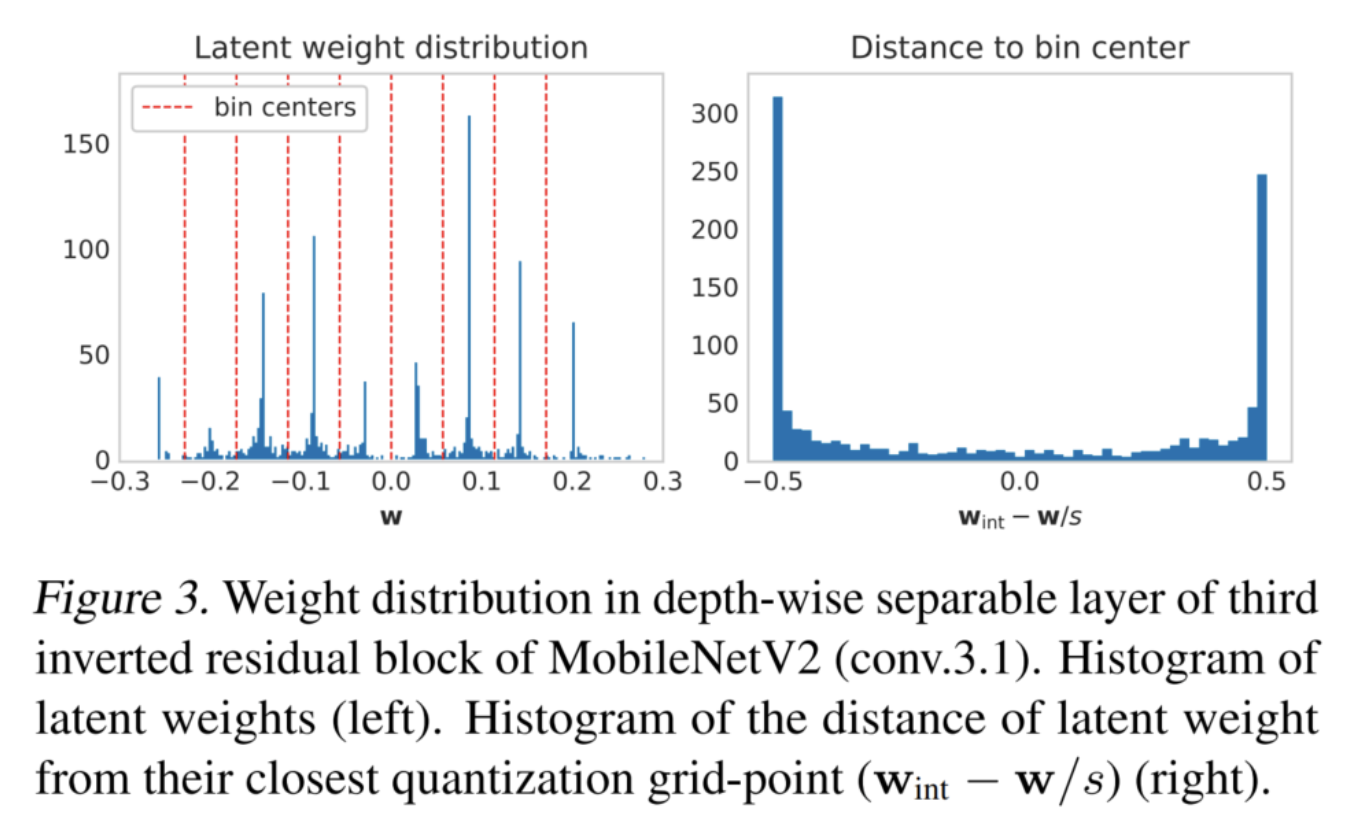
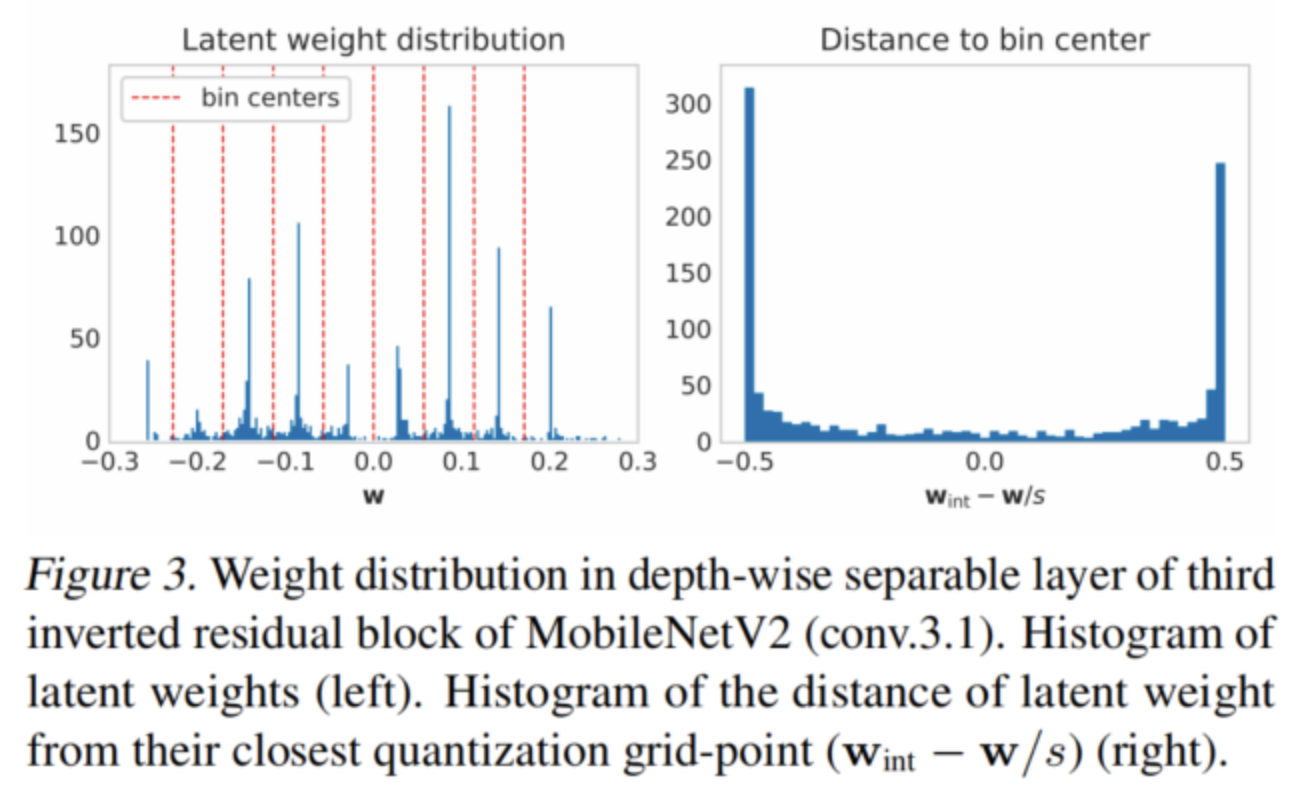
在圖3中還可以看到,在假定的網(wǎng)絡(luò)收斂之后,很大一部分潛在權(quán)重正好位于網(wǎng)格點(diǎn)之間的決策邊界。這進(jìn)一步強(qiáng)化了一個(gè)觀察結(jié)果,即很大一部分權(quán)重會(huì)振蕩而不收斂。
作者確定了與神經(jīng)網(wǎng)絡(luò)訓(xùn)練中的振蕩相關(guān)的2個(gè)主要問(wèn)題:
批量歸一化推理統(tǒng)計(jì)的錯(cuò)誤估計(jì)
對(duì)網(wǎng)絡(luò)優(yōu)化的不利影響
1、批量標(biāo)準(zhǔn)化的影響
在訓(xùn)練批量歸一化過(guò)程中,層跟蹤每層輸出的平均值和方差的指數(shù)移動(dòng)平均值(EMA),以便在推理過(guò)程中用作真實(shí)樣本統(tǒng)計(jì)的近似值。當(dāng)訓(xùn)練全精度神經(jīng)網(wǎng)絡(luò)時(shí),可以預(yù)期權(quán)重在接近收斂時(shí)會(huì)非常緩慢地變化。因此,預(yù)計(jì)每一層的輸出統(tǒng)計(jì)數(shù)據(jù)在迭代過(guò)程中都相當(dāng)穩(wěn)定,因此EMA是統(tǒng)計(jì)數(shù)據(jù)的一個(gè)很好的估計(jì)。
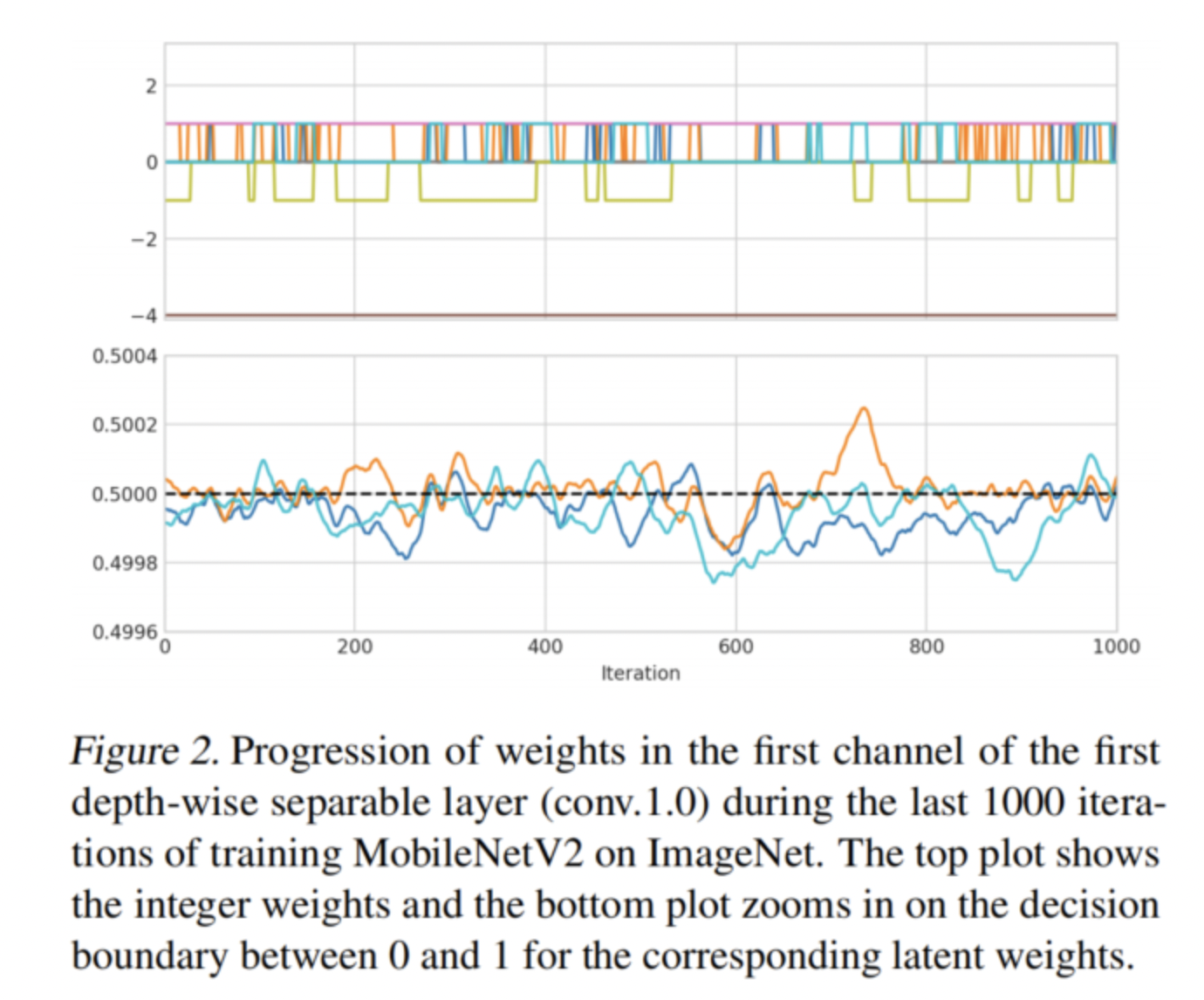
然而,QAT中的振蕩會(huì)導(dǎo)致整數(shù)權(quán)重的快速變化(見圖2),從而導(dǎo)致迭代之間的顯著分布偏移,甚至接近收斂。振蕩引起的輸出分布的突然而大的變化可能會(huì)破壞EMA統(tǒng)計(jì)數(shù)據(jù),導(dǎo)致準(zhǔn)確性的顯著下降。
事實(shí)上,有兩個(gè)因素放大了這種影響:
權(quán)重位寬
每個(gè)輸出通道的權(quán)重?cái)?shù)量
比特寬度越低,量化級(jí)別之間的距離就越大,因?yàn)樗c成比例。當(dāng)振蕩權(quán)重從一個(gè)量化級(jí)別移動(dòng)到另一個(gè)量化級(jí)時(shí),它們?cè)谳敵龇植贾性斐沙杀壤妮^大偏移。第二個(gè)重要因素是每個(gè)輸出通道的權(quán)重?cái)?shù)量。權(quán)重的數(shù)量越小,單個(gè)權(quán)重對(duì)最終累積的貢獻(xiàn)就越大。當(dāng)累積數(shù)量增加時(shí),由于大數(shù)定律,振蕩的影響趨于平均。
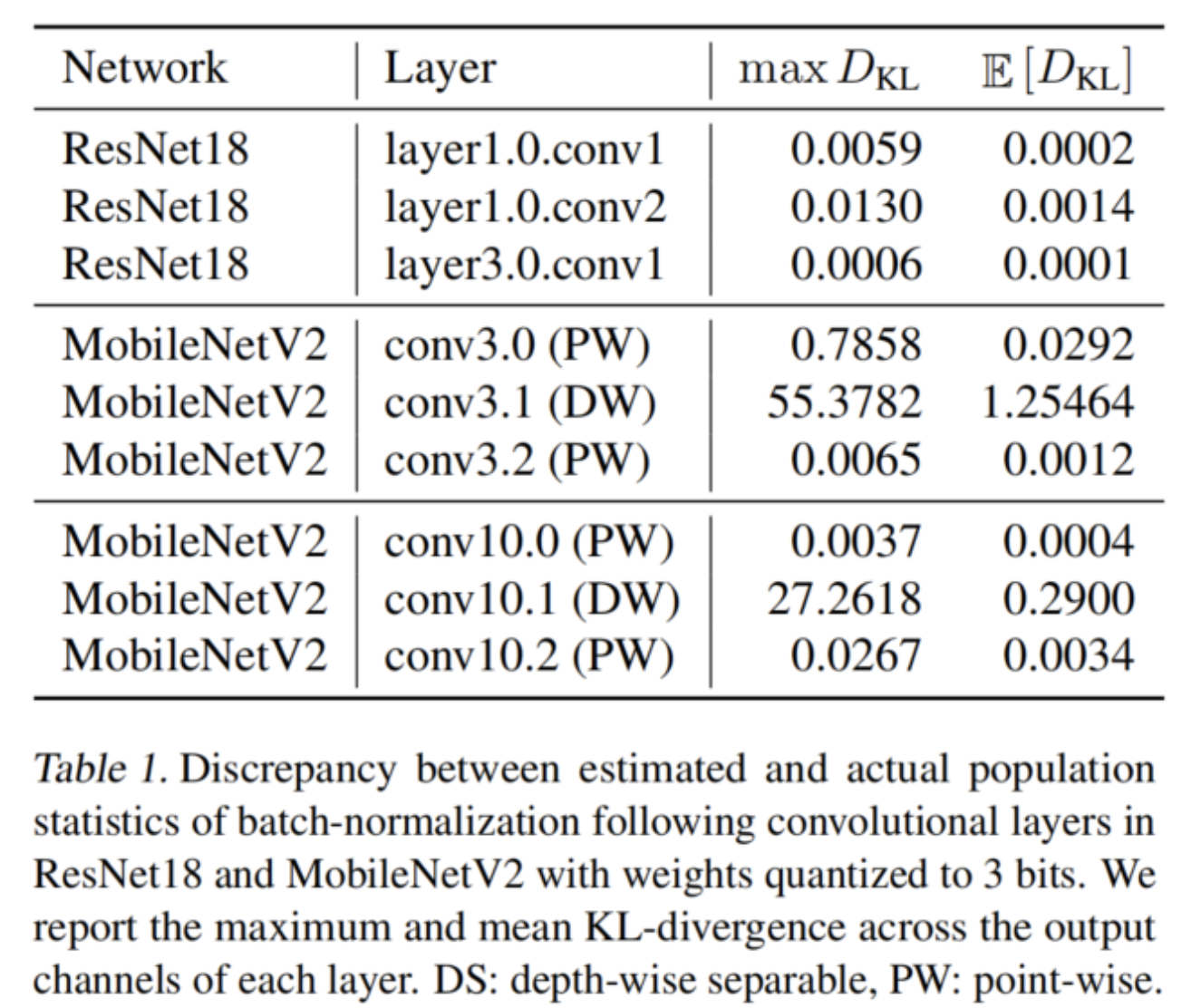
在表1中,使用KL散度來(lái)量化population和 estimated statistics之間的差異,確實(shí)觀察到,與MobileNetV2中的逐點(diǎn)卷積和ResNet18中的全卷積相比,深度可分離層的KL發(fā)散要大得多。
這個(gè)問(wèn)題的一個(gè)簡(jiǎn)單直接的解決方案是在訓(xùn)練后用一小部分?jǐn)?shù)據(jù)重新估計(jì)批量歸一化統(tǒng)計(jì)。這種方法作者稱之為批處理歸一化(BN)重新估計(jì),有時(shí)用于隨機(jī)量化公式。然而,作者認(rèn)為由于振蕩權(quán)重,它在確定性QAT公式中也是必不可少的。
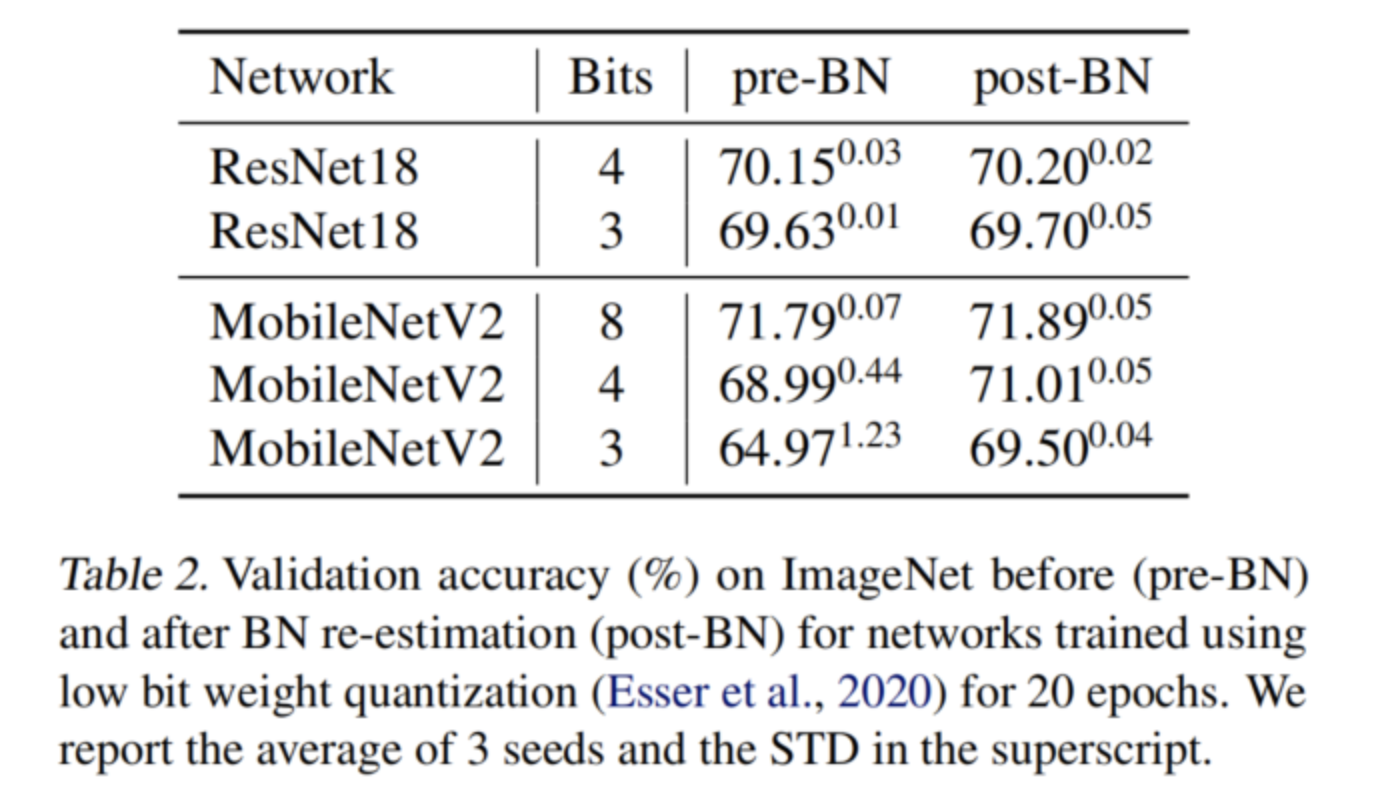
在表2中可以看到BN重新估計(jì)不僅提高了MobileNetV2的最終量化精度,而且降低了不同種子之間的方差。作者進(jìn)一步觀察到,對(duì)于MobileNetV2,隨著比特寬度的減小,精度上的差距變大,而對(duì)于ResNet18,情況并非如此。
2、對(duì)訓(xùn)練的影響
除了損害BN統(tǒng)計(jì)之外,振蕩還可能對(duì)訓(xùn)練過(guò)程本身產(chǎn)生負(fù)面影響。為了說(shuō)明這一點(diǎn),首先表明,如果在兩種振蕩狀態(tài)之間隨機(jī)采樣振蕩權(quán)重,則具有3位權(quán)重的收斂MobileNetV2可以實(shí)現(xiàn)較低的訓(xùn)練損失(和較高的驗(yàn)證精度)。

在表3中給出了這個(gè)實(shí)驗(yàn)的結(jié)果。可以觀察到,采樣網(wǎng)絡(luò)上的平均訓(xùn)練損失與最終收斂模型的平均訓(xùn)練損失相似。然而,許多樣本實(shí)現(xiàn)了較低的訓(xùn)練損失,并且最佳隨機(jī)采樣網(wǎng)絡(luò)顯示出顯著較低的訓(xùn)練損失。
作者還使用AdaRound的自適應(yīng)來(lái)執(zhí)行振蕩權(quán)重的二進(jìn)制優(yōu)化。在最終任務(wù)丟失時(shí)同時(shí)優(yōu)化所有層的舍入,類似于文獻(xiàn)中使用模擬退火來(lái)解決二進(jìn)制優(yōu)化問(wèn)題。可以看到,這種二進(jìn)制優(yōu)化在最佳隨機(jī)樣本和原始收斂網(wǎng)絡(luò)的基礎(chǔ)上顯著改進(jìn)。這表明,權(quán)重振蕩會(huì)阻止網(wǎng)絡(luò)在訓(xùn)練過(guò)程中收斂到最佳局部最小值,并可能對(duì)優(yōu)化過(guò)程不利。
最后,在訓(xùn)練的早期使用振蕩凍結(jié)技術(shù)防止振蕩會(huì)導(dǎo)致比振蕩權(quán)重的二元優(yōu)化更高的驗(yàn)證精度。這表明,振蕩不僅會(huì)阻止QAT在訓(xùn)練結(jié)束時(shí)收斂到最佳局部最小值,而且還會(huì)導(dǎo)致優(yōu)化器在訓(xùn)練早期朝著次優(yōu)方向發(fā)展。
3、克服QAT的振蕩問(wèn)題
既然已經(jīng)確定了振蕩在優(yōu)化過(guò)程中可能會(huì)產(chǎn)生負(fù)面影響,特別是對(duì)于低位量化,所以就把重點(diǎn)放在如何克服它們上。首先,引入了一種用于量化振蕩的度量,然后提出了兩種新的技術(shù),旨在防止在量化感知訓(xùn)練過(guò)程中出現(xiàn)振蕩。
3.1、量化振蕩
在解決振蕩之前,需要一種在訓(xùn)練中檢測(cè)和測(cè)量振蕩的方法。建議使用指數(shù)移動(dòng)平均(EMA)來(lái)計(jì)算隨時(shí)間變化的振蕩頻率。然后,可以將最小頻率定義為振蕩權(quán)重的閾值。對(duì)于在迭代t中發(fā)生的振蕩,需要滿足兩個(gè)條件:

然后,使用指數(shù)移動(dòng)平均(EMA)來(lái)跟蹤隨時(shí)間變化的振蕩頻率:
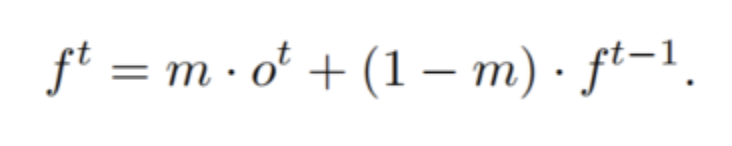
3.2、振蕩阻尼
當(dāng)權(quán)重振蕩時(shí),它們總是在兩個(gè)量化區(qū)間之間的決策閾值附近移動(dòng)。這意味著振蕩權(quán)重總是接近量化bin的邊緣。為了抑制振蕩行為,使用了一個(gè)正則化項(xiàng),該項(xiàng)鼓勵(lì)潛在權(quán)重靠近bin的中心而不是邊緣。將類似于權(quán)重衰減的阻尼損失定義為:

獨(dú)立于標(biāo)度s,因此間接獨(dú)立于位寬。進(jìn)一步將潛在權(quán)重剪裁到量化網(wǎng)格的范圍,使得只有在量化期間沒(méi)有被剪裁的權(quán)重才會(huì)獲得正則化效果。這對(duì)于避免在基于LSQ的范圍學(xué)習(xí)中與量化尺度梯度的任何有害相互作用很重要。這種正則化的缺點(diǎn)是,它不僅影響振蕩的權(quán)重,而且還會(huì)阻礙不處于振蕩狀態(tài)的權(quán)重的移動(dòng)。
3.3、振蕩權(quán)值的迭代凍結(jié)
作者提出了另一種更有針對(duì)性的方法,通過(guò)在訓(xùn)練中凍結(jié)權(quán)重來(lái)防止權(quán)重振蕩。在這種方法中,跟蹤訓(xùn)練期間每個(gè)權(quán)重的振蕩頻率,如方程(4)所述。如果任何權(quán)重的振蕩頻率超過(guò)閾值,該權(quán)重將被凍結(jié),直到訓(xùn)練結(jié)束。在整數(shù)域中應(yīng)用凍結(jié),以便在優(yōu)化過(guò)程中scale 的潛在變化不會(huì)導(dǎo)致不同的舍入。
當(dāng)一個(gè)權(quán)重振蕩時(shí),它不一定在兩種振蕩狀態(tài)下花費(fèi)相等的時(shí)間。正如在第2.2節(jié)的示例中所示,權(quán)重處于每個(gè)狀態(tài)的可能性線性地取決于該量化狀態(tài)與最優(yōu)值的距離。結(jié)果,隨著時(shí)間的推移,所有量化值的期望將對(duì)應(yīng)于最優(yōu)值。一旦權(quán)重的頻率超過(guò)閾值,它就可能處于兩種量化狀態(tài)中的任何一種。為了將權(quán)重凍結(jié)到更頻繁的狀態(tài),使用指數(shù)移動(dòng)平均值(EMA)記錄以前的整數(shù)值。然后,通過(guò)四舍五入EMA將最頻繁的整數(shù)狀態(tài)分配給凍結(jié)權(quán)重。

在算法1中總結(jié)了提出的迭代權(quán)重凍結(jié)。注意,該算法可以與任何基于梯度的優(yōu)化器組合使用,并且不限于特定的量化公式或梯度估計(jì)器。在迭代級(jí)別上凍結(jié)權(quán)重的想法與迭代修剪密切相關(guān),在迭代修剪中,小權(quán)重被迭代修剪(凍結(jié)為零)。
4、實(shí)驗(yàn)
4.1、消融實(shí)驗(yàn)
1、振蕩阻尼
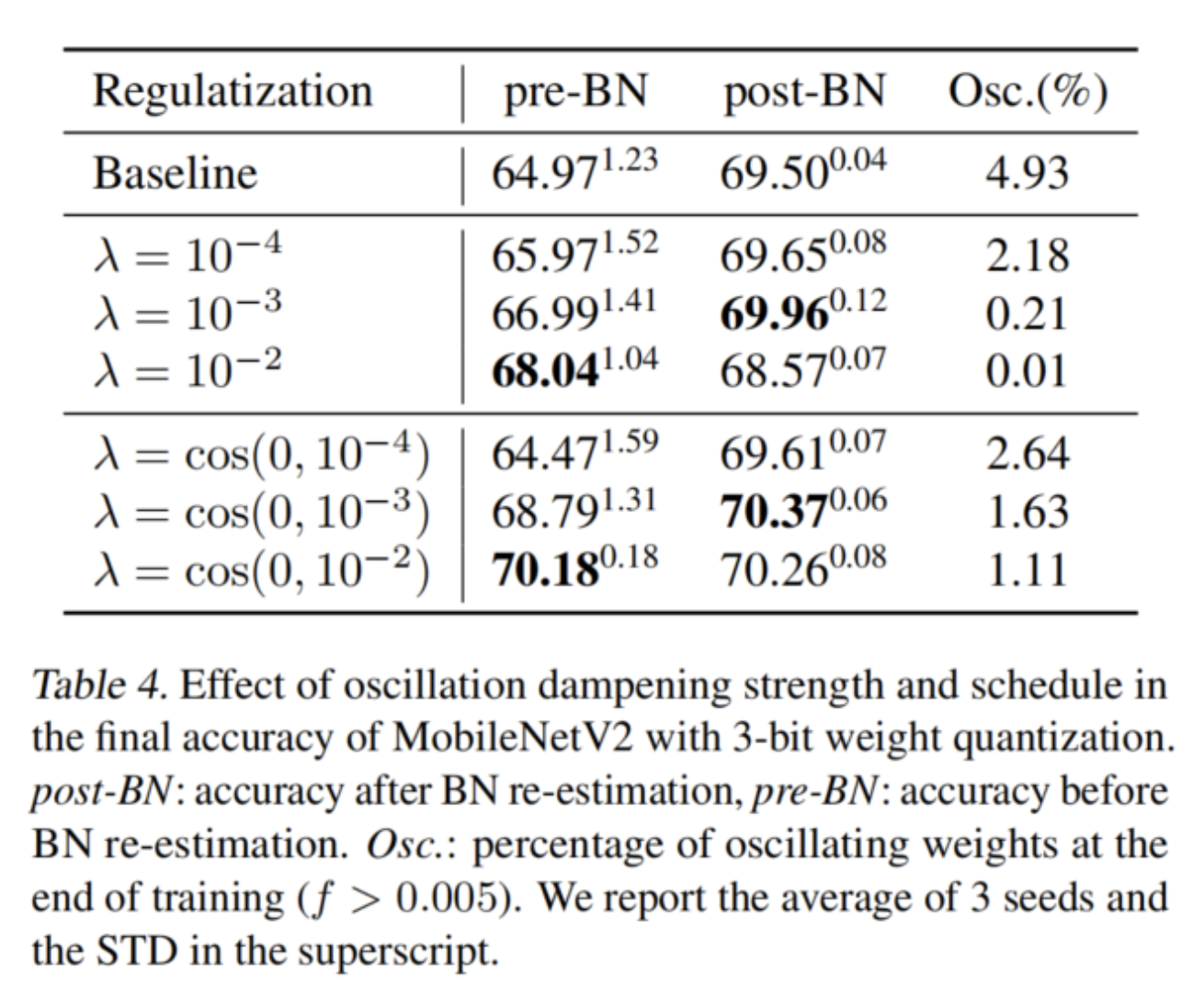
在表4中,作者研究了阻尼損失的強(qiáng)度如何影響網(wǎng)絡(luò)的最終精度以及訓(xùn)練結(jié)束時(shí)振蕩權(quán)重的比例。在前3行中可以觀察到,隨著系數(shù)λ的增加,振蕩權(quán)重的比例降低,BN重新估計(jì)前后的精度差距縮小。然而,過(guò)多的阻尼會(huì)損害最終的精度,這表明過(guò)度的正則化會(huì)抑制權(quán)重在量化級(jí)別之間的有益移動(dòng)。
解決這個(gè)問(wèn)題的方法是在訓(xùn)練過(guò)程中逐漸增加正規(guī)化權(quán)重。這允許潛在權(quán)重在訓(xùn)練的第一階段更自由地移動(dòng),同時(shí)通過(guò)應(yīng)用更強(qiáng)的正則化來(lái)減少接近收斂的有害振蕩。
作者發(fā)現(xiàn)λ的余弦退火計(jì)劃在實(shí)踐中效果良好。Han等人也注意到,這種規(guī)則化在訓(xùn)練的早期階段是有害的,但實(shí)際上采用了兩階段優(yōu)化過(guò)程。這樣的策略可以顯著抑制振蕩,同時(shí)不會(huì)損害準(zhǔn)確性。最佳阻尼配置比BN后重新估計(jì)基線提高了近1%,比BN前重新估計(jì)基線改善了5%以上。
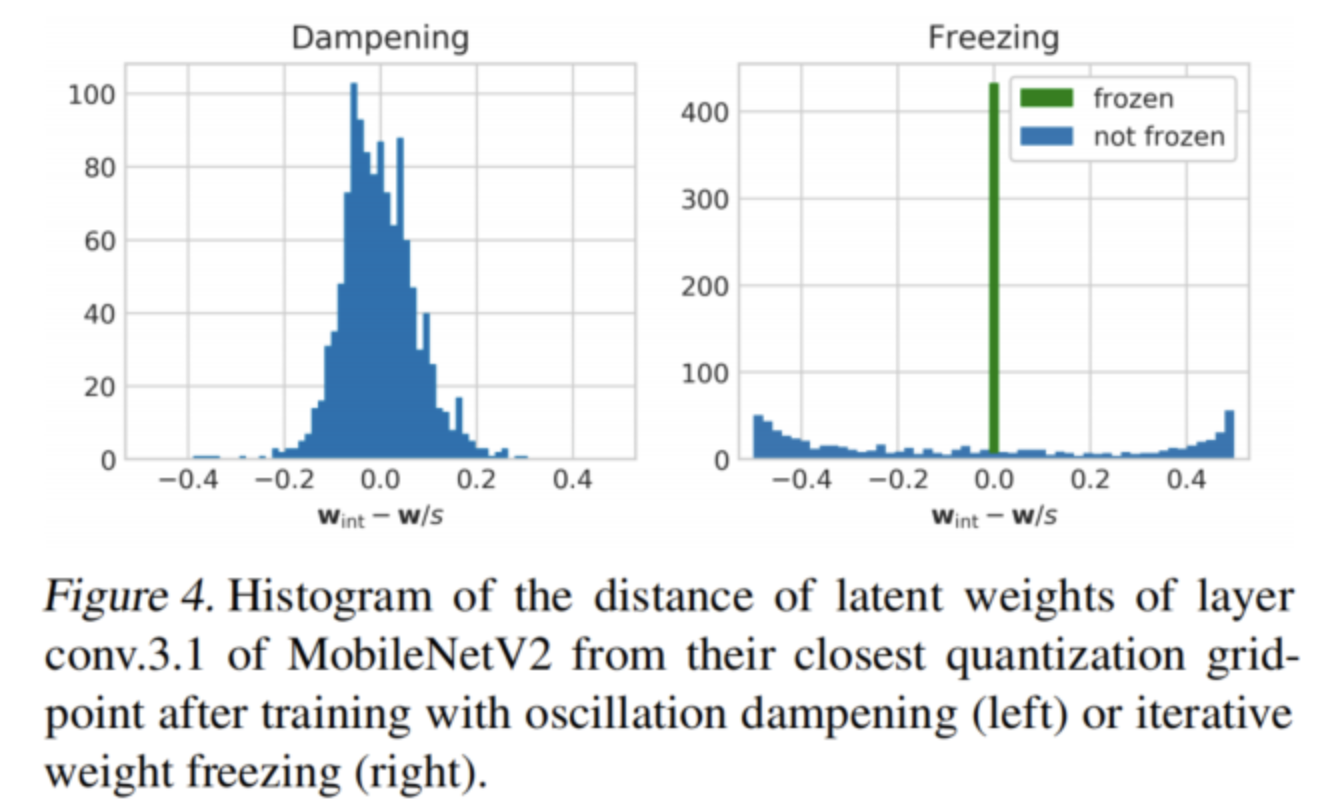
在圖4(左)中還看到了阻尼對(duì)圖3中相同深度可分離層的潛在重量分布的影響。正如預(yù)期的那樣,潛在權(quán)重現(xiàn)在聚集在量化bin中心周圍,在決策邊界幾乎沒(méi)有任何權(quán)重。
2、迭代權(quán)重凍結(jié)
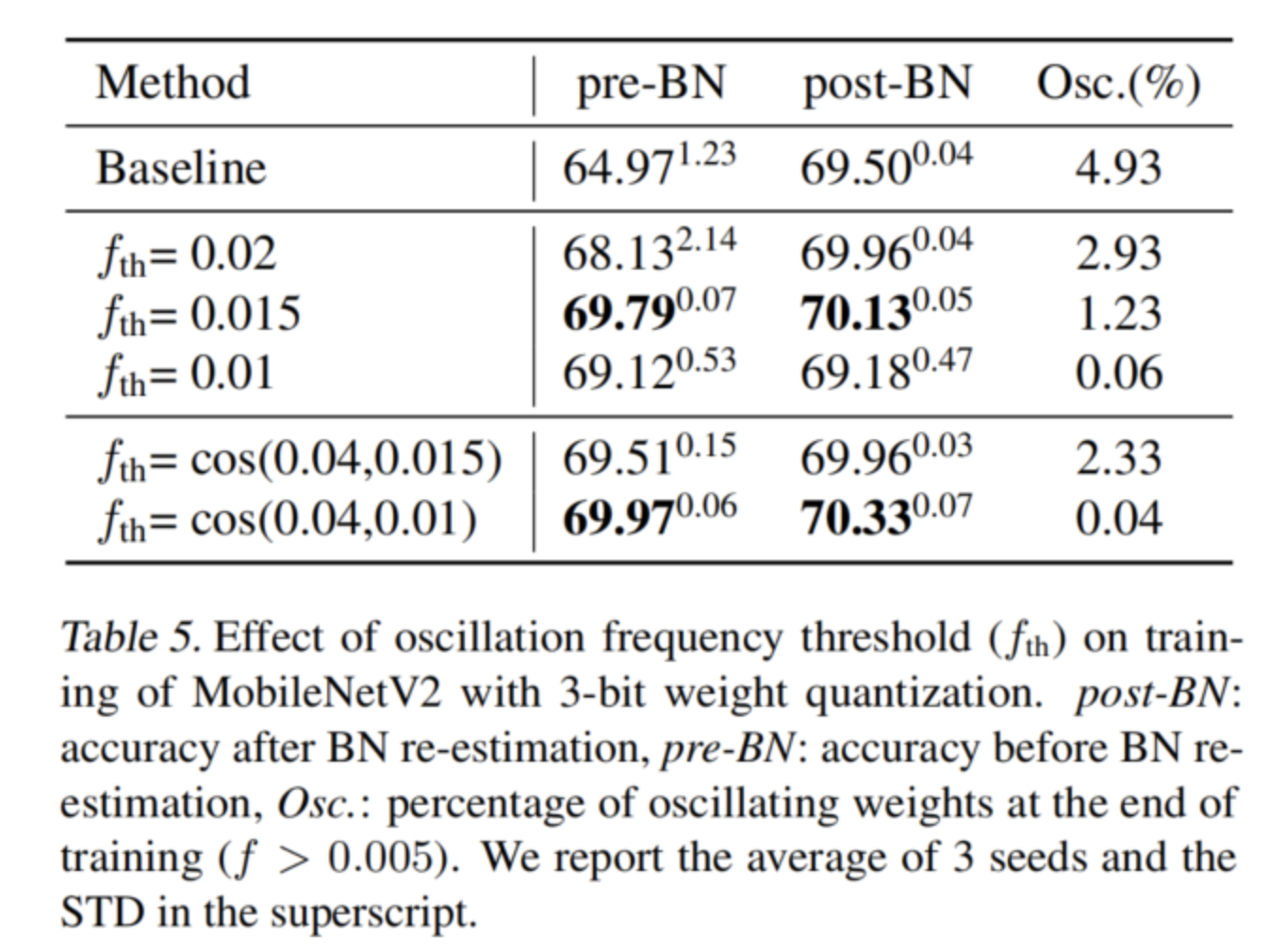
在表5中展示了迭代權(quán)重凍結(jié)算法對(duì)各種凍結(jié)閾值的有效性。在整個(gè)訓(xùn)練過(guò)程中使用恒定的閾值,可以看到殘差振蕩的數(shù)量隨著閾值的降低而顯著減少,并且網(wǎng)絡(luò)中只保留一些低頻振蕩。還可以看到,前BN重新估計(jì)精度更接近后BN重新估計(jì)準(zhǔn)確性,正如人們?cè)谟?xùn)練結(jié)束時(shí)振蕩較少時(shí)所預(yù)期的那樣。
然而,如果振蕩閾值變得太低,那么在訓(xùn)練的早期階段,太多的權(quán)重會(huì)被凍結(jié),從而降低最終的準(zhǔn)確性。為了解決這個(gè)問(wèn)題,對(duì)凍結(jié)閾值應(yīng)用了一個(gè)類似于阻尼中使用的退火計(jì)劃。這能夠使用更強(qiáng)的凍結(jié)閾值,并在訓(xùn)練結(jié)束時(shí)凍結(jié)幾乎所有的振蕩,此時(shí)它們最具破壞性。
最佳凍結(jié)閾值比BN后重新估計(jì)基線提高了近1%,比BN前重新估計(jì)基線改善了5%以上。它的精度與振蕩阻尼相當(dāng),同時(shí)殘差振蕩顯著減少(0.04%對(duì)1.11%)。
在圖4(右)中可以看到迭代權(quán)值凍結(jié)如何改變MobileNetV2的層conv.3.1的潛在權(quán)值分布。大部分潛在權(quán)值現(xiàn)在被凍結(jié)在bin中心,去除在圖3中決策邊界觀察到的峰值。
4.2、與其他QAT方法的比較
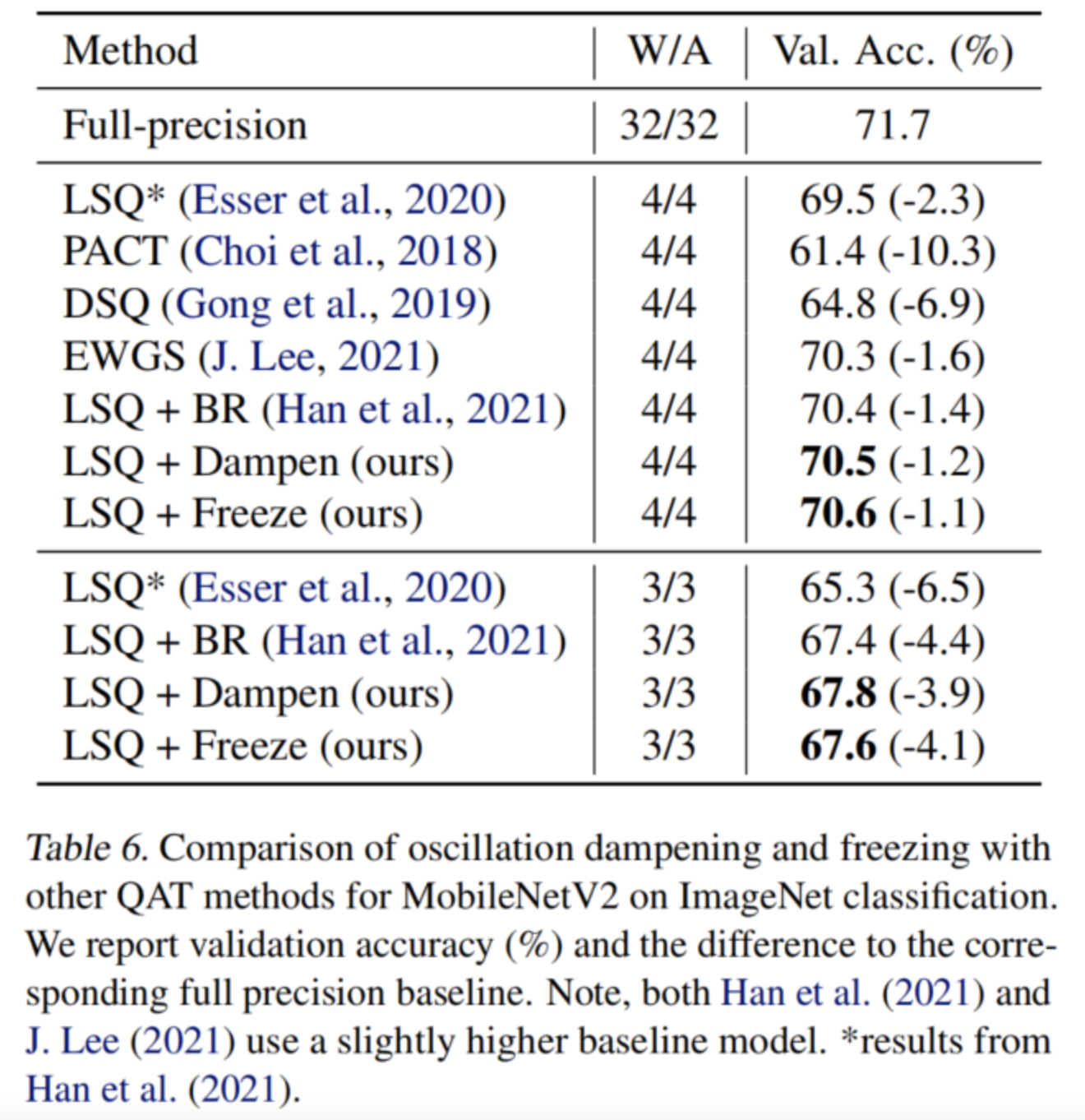
將克服振蕩的方法與其他QAT替代方案進(jìn)行了比較,并證明了它們?cè)诹餍械母咝窠?jīng)網(wǎng)絡(luò)的低比特量化中的有效性。為了與文獻(xiàn)中現(xiàn)有的方法進(jìn)行比較,作者對(duì)權(quán)重和激活進(jìn)行了量化。在表6中展示了MobileNetV2的結(jié)果,并證明兩種算法在3-bits和4-bits量化方面都優(yōu)于文獻(xiàn)中所有競(jìng)爭(zhēng)的QAT技術(shù)。
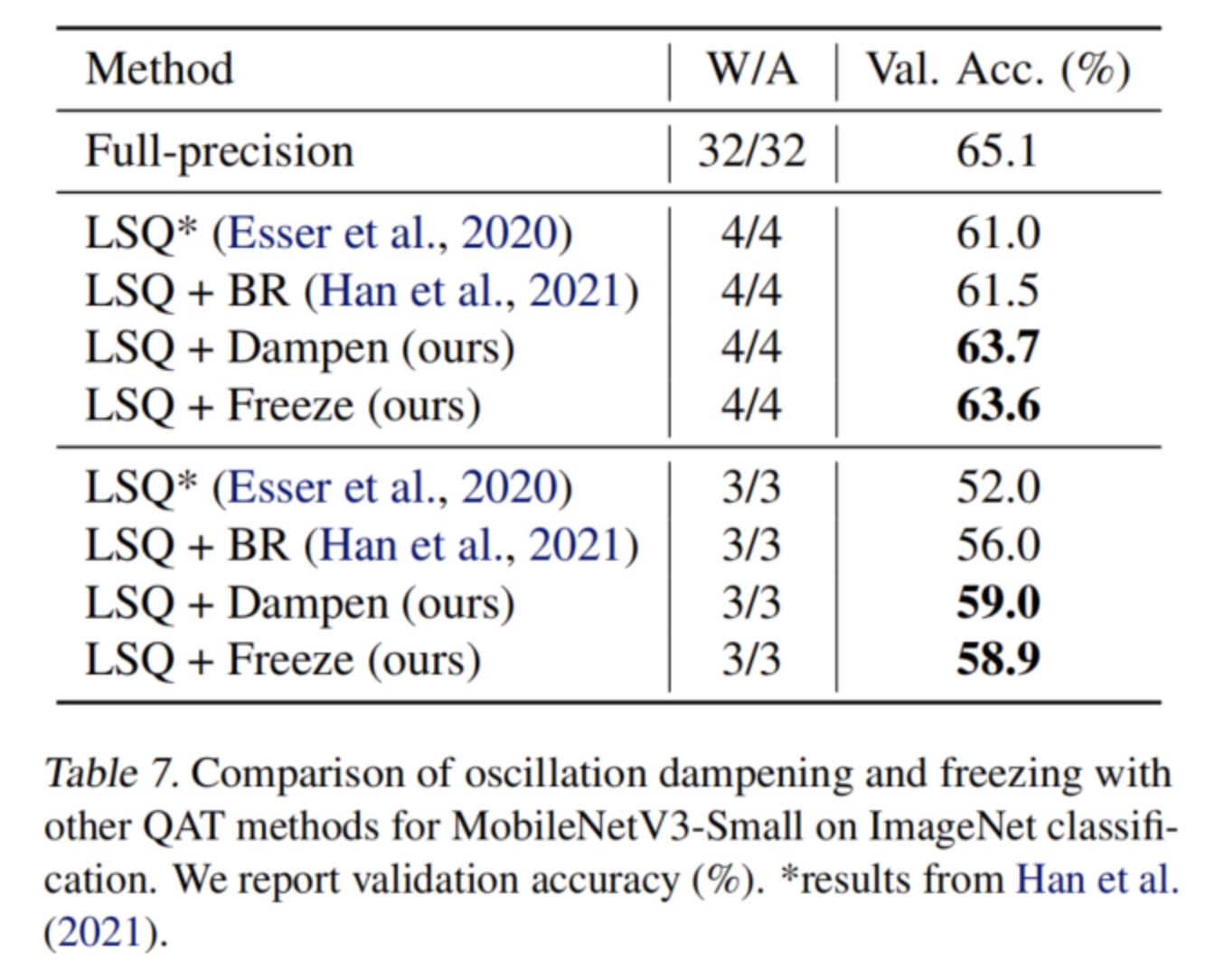
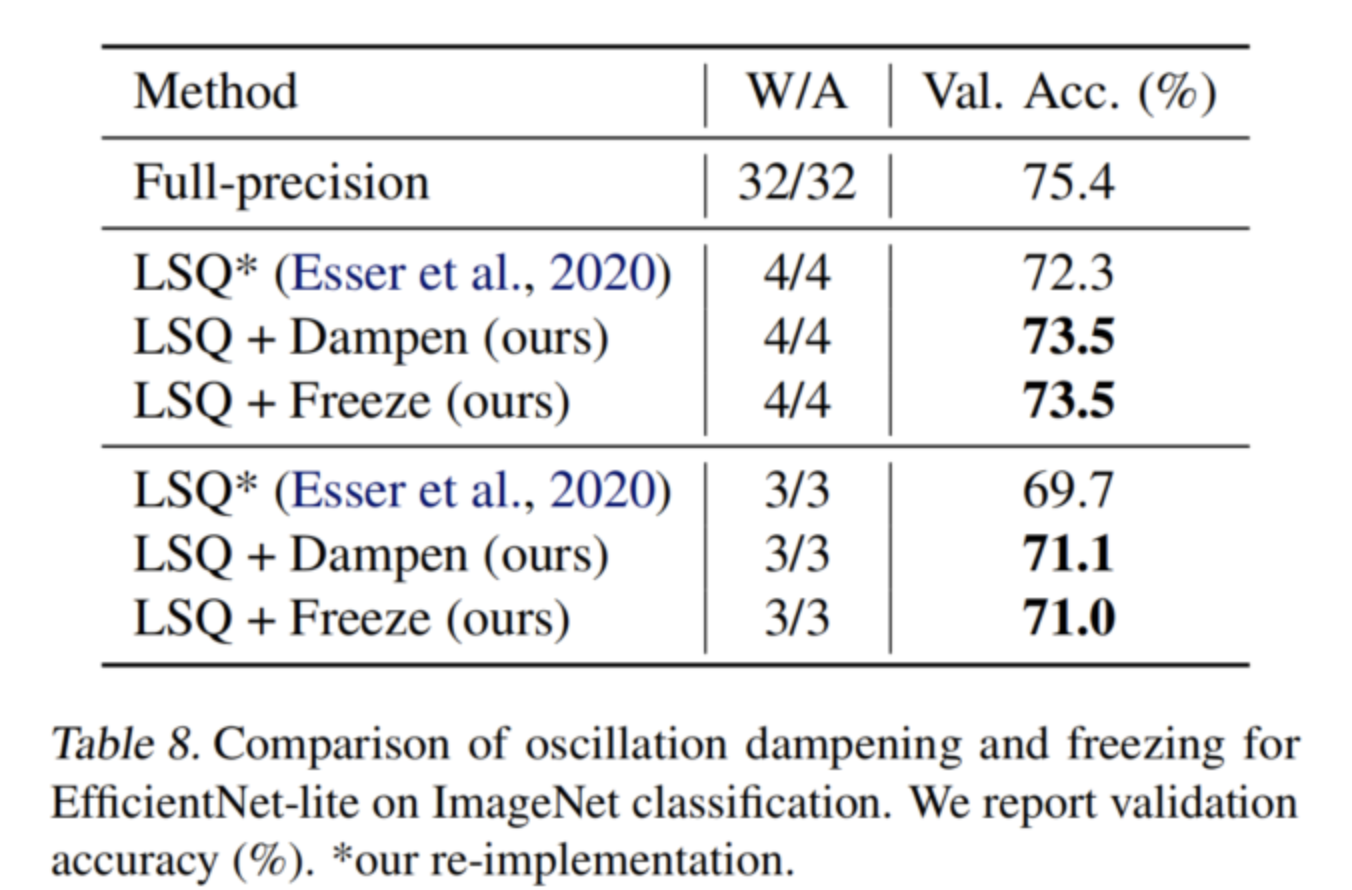
還在表7和表8中分別獲得了MobileNetV3 Small和EfficientNet lite的最新結(jié)果。在所有情況下,本文的振蕩預(yù)防方法都比常用的LSQ基線顯著提高(>1%),表明本文的方法對(duì)其他高效網(wǎng)絡(luò)的普遍適用性。
可以注意到,與LSQ基線相比,振蕩抑制導(dǎo)致訓(xùn)練時(shí)間增加了約33%。另一方面,迭代權(quán)重凍結(jié)在實(shí)現(xiàn)類似性能的同時(shí),計(jì)算開銷可以忽略不計(jì)。
-
振蕩器
+關(guān)注
關(guān)注
28文章
4008瀏覽量
140830 -
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4814瀏覽量
103566
發(fā)布評(píng)論請(qǐng)先 登錄
瑞芯微模型量化文件構(gòu)建
2.0.0版本的ST Edge AI Core在linux平臺(tái)上可以把量化后的onnx模型轉(zhuǎn)換為.nb,但是運(yùn)行報(bào)錯(cuò),缺少文件,為什么?
多層板的焊盤到底應(yīng)該怎么設(shè)計(jì)?華秋一文告訴你
X-CUBE-AI 7.1.0生成代碼初始化錯(cuò)誤如何解決呢?
【KV260視覺入門套件試用體驗(yàn)】Vitis AI 進(jìn)行模型校準(zhǔn)和來(lái)量化
一文告訴你如何用好AD797
一文告訴你芯片材料的新選擇
Google發(fā)布新API,支持訓(xùn)練更小更快的AI模型





 一文告訴你AI模型QAT量化遇到震蕩問(wèn)題應(yīng)該如何解決呢?
一文告訴你AI模型QAT量化遇到震蕩問(wèn)題應(yīng)該如何解決呢?











評(píng)論