使用內點法求解線性規劃問題
在 MATLAB 中,可以使用 fmincon 函數來求解線性規劃問題,其中包括內點法。fmincon 函數的使用方法非常靈活,可以通過修改參數來指定不同的算法、約束條件等。
以下是一個使用內點法求解線性規劃問題的簡單示例:
假設有以下線性規劃問題:
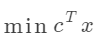
滿足以下約束條件:
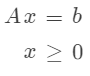
下面是 MATLAB 的代碼實現:
%定義目標函數和線性約束條件 c=[-1;-2;-3]; A=[112;211]; b=[4;5]; lb=[0;0;0]; %調用fmincon函數進行優化 options=optimoptions('fmincon','Algorithm','interior-point','Display','iter'); [x,fval,eflag,output]=fmincon(@(x)c'*x,[],[],[],A,b,lb,[],[],options);
在上面的代碼中,我們指定了 Algorithm 為 'interior-point',即使用內點法求解線性規劃問題。需要注意的是,內點法只能用于求解線性規劃問題。如果要求解非線性規劃問題,可以考慮使用其他算法,例如 SQP 算法、罰函數法等。
此外,對于線性規劃問題,fmincon 函數還支持直接指定目標函數和線性約束條件的形式,例如:
%定義目標函數和線性約束條件
f=[1;2;3];
Aeq=[112;211];
beq=[4;5];
lb=[0;0;0];
%調用fmincon函數進行優化
options=optimoptions('fmincon','Algorithm','interior-point','Display','iter');
[x,fval,eflag,output]=fmincon(f,[],[],[],Aeq,beq,lb,[],[],options);
注意到這里我們使用了 Aeq 和 beq 來指定線性約束條件。這種形式更為直觀,但在一些情況下可能需要進行轉換才能滿足標準形式的要求。
審核編輯:湯梓紅
-
matlab
+關注
關注
187文章
2988瀏覽量
232618 -
算法
+關注
關注
23文章
4675瀏覽量
94198 -
函數
+關注
關注
3文章
4361瀏覽量
63642 -
約束
+關注
關注
0文章
82瀏覽量
12869
原文標題:使用內點法求解線性規劃問題
文章出處:【微信號:嵌入式職場,微信公眾號:嵌入式職場】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
matlab 數學建模
matlab數學建模算法全收錄 799*** 4.7M 超清書簽版
基于整數線性規劃的TTA代碼優化
節點法與網孔法流程圖求解
線性規劃在緩沖區溢出檢測中的應用研究
求解含儲能裝置的微電網動態最優潮流的對偶半定規劃方法
使用MATLAB實現分枝定界法求解整數規劃的詳細資料說明






 使用內點法求解線性規劃問題
使用內點法求解線性規劃問題










評論