當(dāng)涉及到控制系統(tǒng)中的精確調(diào)節(jié)和穩(wěn)定性,PID(比例-積分-微分)控制算法是一種不可或缺的工具。本文將簡(jiǎn)單介紹 PID 控制算法,從基本概念到具體實(shí)現(xiàn),一起了解如何使用 PID 控制算法來優(yōu)化控制系統(tǒng)。
引言
PID(比例-積分-微分)控制算法作為一種廣泛應(yīng)用的控制策略,在自動(dòng)化控制系統(tǒng)中扮演著不可或缺的角色。無論是工業(yè)生產(chǎn)中的溫度控制、機(jī)器人運(yùn)動(dòng)控制,還是飛行器、醫(yī)療設(shè)備等領(lǐng)域,PID 控制都發(fā)揮著重要作用。
PID 控制算法的核心思想在于基于當(dāng)前的誤差、過去的誤差累積和未來的誤差變化來調(diào)整控制輸出,以實(shí)現(xiàn)系統(tǒng)的穩(wěn)定性和響應(yīng)性能。其中,比例項(xiàng)用于快速響應(yīng)誤差的大小,積分項(xiàng)用于消除穩(wěn)態(tài)誤差,而微分項(xiàng)則有助于預(yù)測(cè)系統(tǒng)未來行為,從而改善系統(tǒng)的穩(wěn)定性。這三個(gè)組成部分相互作用,使得 PID 控制能夠在多樣化的應(yīng)用中展現(xiàn)出強(qiáng)大的適應(yīng)性。
然而,調(diào)整 PID 參數(shù)并不是一項(xiàng)簡(jiǎn)單的任務(wù)。不同的系統(tǒng)和應(yīng)用需要不同的參數(shù)設(shè)置,錯(cuò)誤的參數(shù)選擇可能會(huì)導(dǎo)致系統(tǒng)不穩(wěn)定、震蕩或超調(diào)。因此,本文將詳細(xì)介紹不同的調(diào)參方法,從手動(dòng)調(diào)節(jié)到自動(dòng)調(diào)參算法,為讀者提供指導(dǎo)。此外,文章還將通過實(shí)際應(yīng)用案例,深入分析如何根據(jù)具體需求來調(diào)整 PID 參數(shù),從而實(shí)現(xiàn)最佳的控制效果。
除了介紹基本的 PID 控制算法,本文還將涵蓋一些改進(jìn)的 PID 變種,如增強(qiáng)型 PID 和模糊 PID,以應(yīng)對(duì)一些特殊情況下的挑戰(zhàn)。這些改進(jìn)算法在一些復(fù)雜的控制系統(tǒng)中能夠提供更好的性能和穩(wěn)定性。
最后,本文還將提供使用 Python 等編程語言實(shí)現(xiàn) PID 控制算法的示例代碼,幫助讀者更好地理解算法的實(shí)際應(yīng)用。通過結(jié)合理論和實(shí)踐,讀者將能夠掌握 PID 控制算法的原理和實(shí)現(xiàn)方法,為他們?cè)诳刂葡到y(tǒng)中的工作提供有力的支持。
基本概念
比例(P)項(xiàng)
比例項(xiàng)反映了當(dāng)前誤差的大小。它使得控制器對(duì)誤差的變化更為敏感,當(dāng)誤差增大時(shí),控制輸出也會(huì)增大。比例項(xiàng)的引入能夠快速響應(yīng)誤差,但過大的比例系數(shù)可能導(dǎo)致系統(tǒng)的震蕩和不穩(wěn)定。
積分(I)項(xiàng)
積分項(xiàng)消除了系統(tǒng)的穩(wěn)態(tài)誤差,即長(zhǎng)時(shí)間內(nèi)誤差無法完全消除的情況。它通過累積過去的誤差來調(diào)整控制輸出,以便逐步消除穩(wěn)態(tài)誤差。積分項(xiàng)的引入能夠提升系統(tǒng)的穩(wěn)定性,但過大的積分系數(shù)可能導(dǎo)致系統(tǒng)的超調(diào)和震蕩。
微分(D)項(xiàng)
微分項(xiàng)預(yù)測(cè)了未來誤差的變化趨勢(shì),從而幫助系統(tǒng)在誤差發(fā)生變化之前就采取控制動(dòng)作。它的引入有助于抑制系統(tǒng)的震蕩和超調(diào),但過大的微分系數(shù)可能會(huì)導(dǎo)致控制器對(duì)噪聲和干擾過于敏感。
PID 控制算法的組成
PID 控制算法將上述三個(gè)項(xiàng)綜合考慮,通過加權(quán)求和來計(jì)算控制輸出。其數(shù)學(xué)表達(dá)式為:
其中, 是控制輸出, 是當(dāng)前的誤差,、 和 分別是比例、積分和微分系數(shù)。
PID 控制算法的調(diào)參
調(diào)參是 PID 控制算法中關(guān)鍵的一步,合適的參數(shù)設(shè)置可以使系統(tǒng)達(dá)到理想的性能。調(diào)參的過程可能需要依賴實(shí)驗(yàn)、模擬或自動(dòng)調(diào)參算法。其中,常用的調(diào)參方法包括手動(dòng)調(diào)節(jié)、Ziegler-Nichols 方法、優(yōu)化算法等。不同的應(yīng)用領(lǐng)域和系統(tǒng)類型可能需要不同的參數(shù)設(shè)置。
PID 控制算法步驟
PID 算法的計(jì)算步驟可以總結(jié)如下:
- 計(jì)算當(dāng)前誤差(偏差),即期望值與實(shí)際值之差。
- 根據(jù)比例項(xiàng),計(jì)算控制輸出變化量,將比例常數(shù)與當(dāng)前誤差相乘。
- 根據(jù)積分項(xiàng),計(jì)算積分累積值,將積分常數(shù)與誤差的累積值相乘,并將累積值添加到控制輸出。
- 根據(jù)微分項(xiàng),計(jì)算誤差變化率,將微分常數(shù)與誤差變化率相乘,并將結(jié)果添加到控制輸出。
- 將上述三個(gè)項(xiàng)的輸出相加,得到最終的控制輸出。
- 將控制輸出應(yīng)用于系統(tǒng),控制系統(tǒng)的行為,使其接近期望值。
- 根據(jù)系統(tǒng)的響應(yīng),不斷更新和調(diào)整 PID 參數(shù),以達(dá)到更好的控制效果。
通過合理地選擇和調(diào)整比例、積分和微分常數(shù),可以使 PID 算法在不同的控制系統(tǒng)中實(shí)現(xiàn)穩(wěn)定、快速的控制效果。PID 算法的一個(gè)挑戰(zhàn)是如何根據(jù)具體應(yīng)用場(chǎng)景來確定適當(dāng)?shù)膮?shù),這通常需要經(jīng)驗(yàn)和實(shí)驗(yàn)來優(yōu)化。
調(diào)參
調(diào)參是 PID 控制中至關(guān)重要的一步,合適的參數(shù)可以使控制系統(tǒng)達(dá)到最佳性能。調(diào)參通常需要實(shí)驗(yàn)和經(jīng)驗(yàn),以下是一些常用的調(diào)參方法和策略:
- 手動(dòng)調(diào)參: 這是最基本的方法,操作者根據(jù)經(jīng)驗(yàn)和系統(tǒng)特性手動(dòng)調(diào)整 PID 參數(shù)。通常從比例項(xiàng)開始,增大 Kp 以觀察系統(tǒng)響應(yīng)。然后根據(jù)系統(tǒng)的震蕩或過沖情況,逐步調(diào)整積分項(xiàng)和微分項(xiàng)。
- 試錯(cuò)法(試-調(diào)整法): 這是一種迭代的方法,從初始參數(shù)開始,逐步調(diào)整參數(shù)并觀察系統(tǒng)響應(yīng)。根據(jù)系統(tǒng)的性能和穩(wěn)定性,逐步逼近最佳參數(shù)。常見的試錯(cuò)法包括:Ziegler-Nichols 法和 Tyreus-Luyben 法。
- Ziegler-Nichols 方法: 這是一種經(jīng)典的試錯(cuò)法,首先關(guān)閉積分項(xiàng)和微分項(xiàng),僅調(diào)整比例項(xiàng)。從小到大逐步增大 Kp,當(dāng)系統(tǒng)開始震蕩時(shí),記錄此時(shí)的 Kp 值和震蕩周期。然后根據(jù)震蕩周期計(jì)算出 Kp、Ki 和 Kd 的值。
- 專業(yè)軟件工具: 一些工程領(lǐng)域的專業(yè)軟件提供自動(dòng)調(diào)參功能,根據(jù)系統(tǒng)的數(shù)學(xué)模型和實(shí)時(shí)反饋,自動(dòng)計(jì)算出合適的參數(shù)。
- 試驗(yàn)分析: 在實(shí)際系統(tǒng)中進(jìn)行多次試驗(yàn),記錄不同參數(shù)下的系統(tǒng)響應(yīng),并分析數(shù)據(jù)。根據(jù)分析結(jié)果來確定最佳參數(shù)。
- 頻率響應(yīng)法: 通過對(duì)系統(tǒng)進(jìn)行頻率掃描,觀察系統(tǒng)的幅頻響應(yīng)和相頻響應(yīng),從而確定合適的 PID 參數(shù)。
- 模擬仿真: 使用數(shù)學(xué)模型進(jìn)行模擬仿真,通過模擬觀察系統(tǒng)響應(yīng),優(yōu)化參數(shù)。
- 自適應(yīng)控制: 使用自適應(yīng)控制算法,根據(jù)系統(tǒng)的實(shí)時(shí)狀態(tài)和響應(yīng)調(diào)整 PID 參數(shù)。
- 在線優(yōu)化: 在實(shí)際運(yùn)行過程中,實(shí)時(shí)監(jiān)測(cè)系統(tǒng)性能,根據(jù)實(shí)時(shí)數(shù)據(jù)不斷調(diào)整 PID 參數(shù),以適應(yīng)系統(tǒng)變化。
無論使用哪種方法,調(diào)參都需要耐心和實(shí)驗(yàn)。在調(diào)參過程中,要注意以下幾點(diǎn):
- 穩(wěn)定性: 確保調(diào)整后的參數(shù)不會(huì)引起系統(tǒng)的不穩(wěn)定性。
- 過沖和震蕩: 避免過大的比例增益和微分增益引起系統(tǒng)的過沖和震蕩。
- 積分飽和: 積分項(xiàng)可能導(dǎo)致積分飽和問題,導(dǎo)致系統(tǒng)響應(yīng)變慢或不穩(wěn)定。
- 系統(tǒng)動(dòng)態(tài): 考慮系統(tǒng)的動(dòng)態(tài)特性,不同的系統(tǒng)可能需要不同的參數(shù)。
調(diào)參是一個(gè)實(shí)踐和經(jīng)驗(yàn)的過程,需要多次嘗試和調(diào)整,以找到最適合特定應(yīng)用的 PID 參數(shù)。
python 示例
本節(jié)提供一個(gè)使用 Python 編程語言實(shí)現(xiàn) PID 控制算法的示例代碼,并解釋如何在實(shí)際系統(tǒng)中集成 PID 控制算法。
class PIDController:
def __init__(self, kp, ki, kd):
self.kp = kp
self.ki = ki
self.kd = kd
self.prev_error = 0
self.integral = 0
def update(self, setpoint, current_value):
error = setpoint - current_value
self.integral += error
derivative = error - self.prev_error
output = self.kp * error + self.ki * self.integral + self.kd * derivative
self.prev_error = error
return output
# Example usage
pid = PIDController(kp=1.0, ki=0.1, kd=0.01)
setpoint = 50
current_value = 30
for _ in range(100):
control_output = pid.update(setpoint, current_value)
# Apply control_output to the system
# Update current_value based on system's response
print("Control Output:", control_output)
集成 PID 控制算法:
- 確定系統(tǒng)模型: 在實(shí)際系統(tǒng)中集成 PID 控制算法的第一步是了解系統(tǒng)的動(dòng)態(tài)特性,并建立一個(gè)合適的數(shù)學(xué)模型。
- 選擇 PID 參數(shù): 根據(jù)系統(tǒng)的響應(yīng)特性和控制要求,選擇合適的 PID 參數(shù)。可以使用調(diào)參方法進(jìn)行初始參數(shù)選擇,然后進(jìn)行現(xiàn)場(chǎng)調(diào)整。
- 編寫 PID 控制器類: 編寫一個(gè) PID 控制器類,其中包含了 PID 參數(shù)和控制邏輯的實(shí)現(xiàn)。這可以是一個(gè)獨(dú)立的 Python 類或函數(shù)。
- 傳感器和執(zhí)行器接口: 將系統(tǒng)的傳感器和執(zhí)行器與 PID 控制器接口對(duì)接。傳感器提供實(shí)際的系統(tǒng)狀態(tài)信息,執(zhí)行器接收 PID 控制器的輸出并執(zhí)行動(dòng)作。
- 實(shí)時(shí)控制循環(huán): 在主控制循環(huán)中,持續(xù)獲取傳感器數(shù)據(jù),將其輸入 PID 控制器,得到控制輸出,然后將輸出傳遞給執(zhí)行器。這個(gè)循環(huán)通常以一定的時(shí)間間隔運(yùn)行,以實(shí)現(xiàn)實(shí)時(shí)控制。
- 參數(shù)調(diào)整和優(yōu)化: 在實(shí)際運(yùn)行中,監(jiān)測(cè)系統(tǒng)的響應(yīng)并進(jìn)行 PID 參數(shù)調(diào)整。根據(jù)系統(tǒng)的實(shí)際表現(xiàn),可以使用手動(dòng)調(diào)整或自動(dòng)調(diào)參算法來優(yōu)化 PID 參數(shù)。
- 系統(tǒng)穩(wěn)定性和魯棒性測(cè)試: 在集成過程中,進(jìn)行系統(tǒng)穩(wěn)定性測(cè)試和魯棒性測(cè)試。這涉及到系統(tǒng)對(duì)參數(shù)變化和外部干擾的響應(yīng)。
- 迭代和改進(jìn): 根據(jù)實(shí)際測(cè)試結(jié)果,可能需要進(jìn)行多次迭代和改進(jìn),以確保系統(tǒng)達(dá)到所需的性能指標(biāo)。
在實(shí)際應(yīng)用中,集成 PID 控制算法需要結(jié)合領(lǐng)域知識(shí)、系統(tǒng)特性和控制要求。通過不斷的實(shí)驗(yàn)和調(diào)整,可以使系統(tǒng)穩(wěn)定、響應(yīng)迅速,并達(dá)到預(yù)期的控制效果。
比如,仿真一個(gè)簡(jiǎn)單倒立擺系統(tǒng),可以使用如下代碼:
import numpy as np
import matplotlib.pyplot as plt
# Constants
g = 9.81 # Acceleration due to gravity (m/s^2)
m = 1.0 # Mass of the pendulum (kg)
l = 1.0 # Length of the pendulum (m)
c = 0.1 # Damping coefficient
# PID parameters
kp = 100.0
ki = 0.0
kd = 0.0
# Initial conditions
theta0 = np.pi / 4 # Initial angle of the pendulum (45 degrees)
theta_dot0 = 0.0 # Initial angular velocity
# Time parameters
dt = 0.01 # Time step
total_time = 10.0 # Total simulation time
# Initialize variables
theta = theta0
theta_dot = theta_dot0
integral = 0
prev_error = 0
# Lists to store data for plotting
time_values = []
angle_values = []
for t in np.arange(0, total_time, dt):
# Calculate error and integral
error = -theta
integral += error * dt
# Calculate derivative
derivative = (error - prev_error) / dt
# Calculate control input using PID formula
control_input = kp * error + ki * integral + kd * derivative
# Update system dynamics using Euler's method
theta_double_dot = -g / l * np.sin(theta) - c / (m * l**2) * theta_dot + control_input
theta_dot += theta_double_dot * dt
theta += theta_dot * dt
# Store data for plotting
time_values.append(t)
angle_values.append(theta)
# Update previous error for derivative term
prev_error = error
# Plot results
plt.plot(time_values, angle_values)
plt.xlabel('Time (s)')
plt.ylabel('Angle (radians)')
plt.title('Inverted Pendulum Control using PID')
plt.grid(True)
plt.show()
結(jié)果如下:
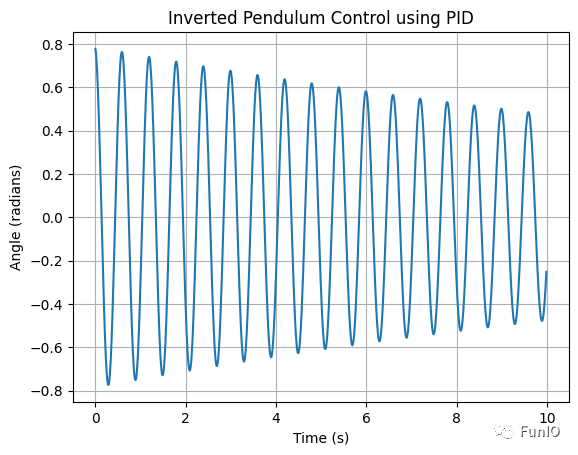
kp = 100.0, ki = 0.0, kd = 0.0
試了幾次,保持 kp 不變,ki = 0.1, kd = 50.0,結(jié)果如下:
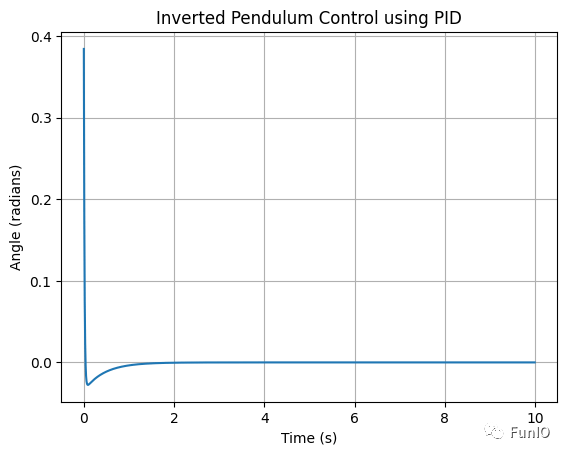
kp = 100.0, ki = 0.1, kd = 50.0
這個(gè)波形是不是有些眼熟?沒錯(cuò),跟 dcdc 穩(wěn)壓輸出的波形很像!
局限和改進(jìn)
局限性:
- 線性假設(shè): PID 控制是基于線性模型的假設(shè),對(duì)于非線性系統(tǒng)可能不適用或需要更復(fù)雜的控制方法。
- 固定參數(shù): 傳統(tǒng) PID 控制的參數(shù)是固定的,難以應(yīng)對(duì)系統(tǒng)參數(shù)變化或外部干擾。
- 復(fù)雜系統(tǒng): 在復(fù)雜的多變量系統(tǒng)中,單一的 PID 控制往往難以滿足需求。
- 不穩(wěn)定性: 不正確的參數(shù)調(diào)整可能導(dǎo)致系統(tǒng)的不穩(wěn)定,甚至失控。
- 不適合開環(huán)系統(tǒng): 對(duì)于開環(huán)系統(tǒng)(無反饋)或系統(tǒng)穩(wěn)定性差的情況,PID 控制效果有限。
改進(jìn)方法:
- 自適應(yīng) PID: 自適應(yīng) PID 控制根據(jù)系統(tǒng)實(shí)際響應(yīng)動(dòng)態(tài)調(diào)整 PID 參數(shù),適應(yīng)系統(tǒng)變化。
- 增加前饋控制: 前饋控制能夠在系統(tǒng)發(fā)生變化前預(yù)先調(diào)整控制輸出,提高系統(tǒng)的響應(yīng)速度和穩(wěn)定性。
- 模糊 PID: 將模糊邏輯與 PID 結(jié)合,使控制更適應(yīng)復(fù)雜和非線性系統(tǒng)。
- 神經(jīng)網(wǎng)絡(luò) PID: 使用神經(jīng)網(wǎng)絡(luò)模型來優(yōu)化 PID 參數(shù),適應(yīng)更廣泛的系統(tǒng)。
- 非線性 PID: 使用非線性 PID 方法,如廣義 PID,能夠更好地應(yīng)對(duì)非線性系統(tǒng)。
- 魯棒 PID: 魯棒 PID 控制考慮到參數(shù)不確定性和外部擾動(dòng),增強(qiáng)系統(tǒng)的穩(wěn)定性和魯棒性。
- 模型預(yù)測(cè)控制: 使用系統(tǒng)的數(shù)學(xué)模型進(jìn)行預(yù)測(cè),優(yōu)化控制輸出,適用于復(fù)雜動(dòng)態(tài)系統(tǒng)。
- 優(yōu)化算法: 使用優(yōu)化算法,如遺傳算法、粒子群算法等,自動(dòng)尋找最佳 PID 參數(shù)。
- 混合控制: 將多個(gè)控制方法結(jié)合,形成混合控制策略,以應(yīng)對(duì)復(fù)雜系統(tǒng)。
- 現(xiàn)代控制理論: 使用現(xiàn)代控制理論,如狀態(tài)反饋、輸出反饋等,適應(yīng)多變量和復(fù)雜系統(tǒng)。
盡管傳統(tǒng) PID 控制在許多應(yīng)用中仍然有效,但針對(duì)局限性和需求,不斷發(fā)展的改進(jìn)方法能夠使控制系統(tǒng)更加穩(wěn)定、快速和適應(yīng)不同情況。
-
控制系統(tǒng)
+關(guān)注
關(guān)注
41文章
6768瀏覽量
111890 -
PID
+關(guān)注
關(guān)注
37文章
1480瀏覽量
87557 -
編程語言
+關(guān)注
關(guān)注
10文章
1955瀏覽量
36280 -
控制算法
+關(guān)注
關(guān)注
4文章
170瀏覽量
22174 -
python
+關(guān)注
關(guān)注
56文章
4825瀏覽量
86374
發(fā)布評(píng)論請(qǐng)先 登錄
PID電機(jī)控制系統(tǒng)(控制原理+控制算法+程序范例)
【技術(shù)干貨】PID算法原理分析及優(yōu)化
模糊PID控制算法如何控制勻速升溫
智能PID算法在液位控制系統(tǒng)中的應(yīng)用
常用的PID控制系統(tǒng)技術(shù)及仿真
基于數(shù)字PID控制算法的溫度控制系統(tǒng)
位置式PID控制算法研究
基于Matlab的網(wǎng)絡(luò)控制系統(tǒng)模糊控制算法應(yīng)用研究
基于模糊PID算法的船舶錨機(jī)控制系統(tǒng)設(shè)計(jì)_李元貴
基于增量式PID算法的帆板控制系統(tǒng)的設(shè)計(jì)張存吉
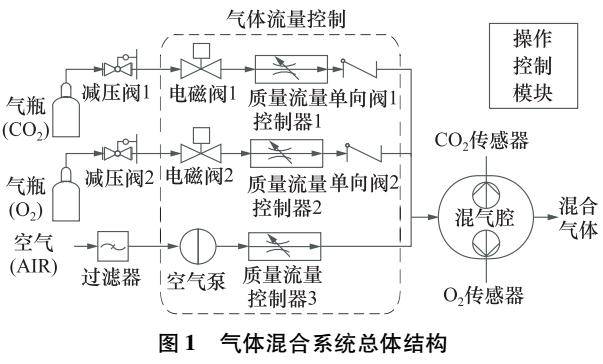
基于改進(jìn)遺傳算法的氣體混合控制系統(tǒng)的設(shè)計(jì)與仿真
如何使用免疫粒子群優(yōu)化算法實(shí)現(xiàn)增量式的PID控制
PID算法在控制系統(tǒng)中的特性和指標(biāo)






 如何使用PID控制算法優(yōu)化控制系統(tǒng)
如何使用PID控制算法優(yōu)化控制系統(tǒng)










評(píng)論