隨著數據集的規模和復雜性的增長,特征或維度的數量往往變得難以處理,導致計算需求增加,潛在的過擬合和模型可解釋性降低。降維技術提供了一種補救方法,它捕獲數據中的基本信息,同時丟棄冗余或信息較少的特征。
這個過程不僅簡化了計算任務,還有助于可視化數據趨勢,減輕維度詛咒的風險,并提高機器學習模型的泛化性能。降維在各個領域都有應用,從圖像和語音處理到金融和生物信息學,在這些領域,從大量數據集中提取有意義的模式對于做出明智的決策和建立有效的預測模型至關重要。
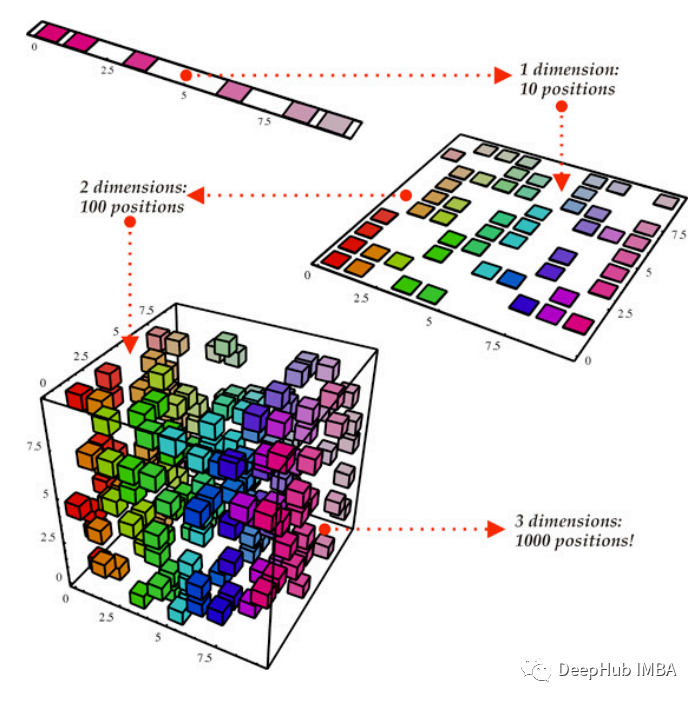
本文將深入研究三種強大的降維技術——主成分分析(PCA)、線性判別分析(LDA)和奇異值分解(SVD)。我們不僅介紹這些方法的基本算法,而且提供各自的優點和缺點。
主成分分析(PCA)
主成分分析(PCA)是一種廣泛應用于數據分析和機器學習的降維技術。它的主要目標是將高維數據轉換為低維表示,捕獲最重要的信息。
我們的目標是識別數據集中的模式,所以希望數據分布在每個維度上,并且在這些維度之間是有獨立性的。方差作為可變性的度量標準,本質上量化了數據集分散的程度。用數學術語來說,它表示與平均的平均平方偏差。計算方差的公式用var(x)表示如下:

協方差量化了兩組有序數據中對應元素相似的程度。用cov(x, y)表示變量x和y之間的協方差。xi表示第i維中x的值,而x柱和y柱表示它們各自的平均值。如果我們有一個維數為m*n的矩陣X,其中包含n個數據點,每個數據點有m維,那么協方差矩陣可以計算如下:

協方差矩陣包括
- 以尺寸方差為主要對角線元素
- 維度的協方差作為非對角線元素
我們的目標是確保數據廣泛分散,表明其維度之間的高方差,另外一個目標是消除相關維度,這意味著維度之間的協方差應為零(表明它們的線性無關)。所以對數據進行變換的目的是使其協方差矩陣具有以下特征:
- 作為主要對角線元素的顯著值。
- 零值作為非對角線元素。
所以必須對原始數據點進行變換獲得類似于對角矩陣的協方差矩陣。將矩陣轉換成對角矩陣的過程稱為對角化,它構成了主成分分析(PCA)背后的主要動機。
PCA的工作原理
1、標準化
當特征以不同的單位度量時,對數據進行標準化。這需要減去平均值,然后除以每個特征的標準差。對具有不同尺度特征的數據進行標準化的失敗可能導致誤導性的成分。
2、計算協方差矩陣
如前面討論的那樣計算協方差矩陣
3、計算特征向量和特征值
確定協方差矩陣的特征向量和特征值。

特征向量表示方向(主成分),特征值表示這些方向上的方差大小。
4、特征值排序
對特征值按降序排序。與最高特征值相對應的特征向量是捕獲數據中最大方差的主成分。
5、選擇主成分
根據需要解釋的方差選擇前k個特征向量(主成分)。一般情況下會設定閾值,保留總方差的很大一部分,例如85%。
6、轉換數據
我們可以用特征向量變換原始數據:
如果我們有m維的n個數據點X: m*n
P: k*m
Y = PX: (km)(mn) = (k*n)
新變換矩陣有n個數據點,有k維。
優點
降維:PCA有效地減少了特征的數量,這對遭受維數詛咒的模型是有益的。
特征獨立性:主成分是正交的(不相關的),這意味著它們捕獲獨立的信息,簡化了對約簡特征的解釋。
降噪:PCA可以通過專注于解釋數據中最顯著方差的成分來幫助減少噪聲。
可視化:降維數據可以可視化,有助于理解底層結構和模式。
缺點
原始特征的可解釋性可能在變換后的空間中丟失,因為主成分是原始特征的線性組合。
PCA假設變量之間的關系是線性的,但并非在所有情況下都是如此。
PCA對特征的尺度比較敏感,因此常常需要標準化。
異常值可以顯著影響PCA的結果,因為它側重于捕獲最大方差,這可能受到極值的影響。
何時使用
高維數據:PCA在處理具有大量特征的數據集以減輕維度詛咒時特別有用。
共線的特點:當特征高度相關時,PCA可以有效地捕獲共享信息并用更少的組件表示它。
可視化:它將數據投射到一個較低維度的空間,可以很容易地可視化。
線性關系:當變量之間的關系大多是線性的,主成分分析是一個合適的技術。
Python代碼示例
import numpy as np
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
# Load iris dataset as an example
iris = load_iris()
X = iris.data
y = iris.target
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Standardize the data (important for PCA)
scaler = StandardScaler()
X_train_std = scaler.fit_transform(X_train)
X_test_std = scaler.transform(X_test)
# Apply PCA
pca = PCA()
X_train_pca = pca.fit_transform(X_train_std)
# Calculate the cumulative explained variance
cumulative_variance_ratio = np.cumsum(pca.explained_variance_ratio_)
# Determine the number of components to keep for 85% variance explained
n_components = np.argmax(cumulative_variance_ratio >= 0.85) + 1
# Apply PCA with the selected number of components
pca = PCA(n_components=n_components)
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
# Display the results
print("Original Training Data Shape:", X_train.shape)
print("Reduced Training Data Shape (PCA):", X_train_pca.shape)
print("Number of Components Selected:", n_components)
上面代碼在最初應用PCA()時沒有指定組件的數量,這意味著它將保留所有組件。然后使用np.cumsum(pca.explained_variance_ratio_)計算累計解釋方差。確定解釋至少85%方差所需的分量數,并使用選定的分量數再次應用PCA。請注意PCA只應用于訓練數據,然后在測試數據應用轉換方法即可。
線性判別分析(LDA)
線性判別分析(LDA)作為一種降維和分類技術,目標是優化數據集中不同類別之間的區別。LDA在預先確定數據點類別的監督學習場景中特別流行。PCA被認為是一種“無監督”算法,它忽略了類標簽,專注于尋找主成分以最大化數據集方差,而LDA則采用“監督”方法。LDA計算“線性判別器”,確定作為軸的方向,以最大限度地分離多個類。我們這里使用“Iris”數據集的示例來了解LDA是如何計算的。它包含了來自三個不同物種的150朵鳶尾花的尺寸。
Iris數據集中有三個類:
- Iris-setosa (n=50)
- Iris-versicolor (n=50)
- Iris-virginica (n=50)
有四個特征:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
LDA的工作步驟
1、計算三種不同花類的平均向量mi, (i=1,2,3):
Mean Vector class 1: [ 5.006 3.418 1.464 0.244]
Mean Vector class 2: [ 5.936 2.77 4.26 1.326]
Mean Vector class 3: [ 6.588 2.974 5.552 2.026]
每個向量包含特定類的數據集中4個特征的平均值。
2、計算類內散點矩陣(Sw),它表示每個類內數據的分布

結果如下:
within-class Scatter Matrix:
[[ 38.9562 13.683 24.614 5.6556]
[ 13.683 17.035 8.12 4.9132]
[ 24.614 8.12 27.22 6.2536]
[ 5.6556 4.9132 6.2536 6.1756]]
3、計算類間散點矩陣(Sb), Sb表示不同類之間的分布,公式如下:

結果如下:
between-class Scatter Matrix:
[[ 63.2121 -19.534 165.1647 71.3631]
[ -19.534 10.9776 -56.0552 -22.4924]
[ 165.1647 -56.0552 436.6437 186.9081]
[ 71.3631 -22.4924 186.9081 80.6041]]
4、計算Sw-1Sb的特征值和特征向量(類似于PCA)。在我們的例子中,有4個特征值和特征向量
Eigenvector 1:
[[-0.2049]
[-0.3871]
[ 0.5465]
[ 0.7138]]
Eigenvalue 1: 3.23e+01
Eigenvector 2:
[[-0.009 ]
[-0.589 ]
[ 0.2543]
[-0.767 ]]
Eigenvalue 2: 2.78e-01
Eigenvector 3:
[[ 0.179 ]
[-0.3178]
[-0.3658]
[ 0.6011]]
Eigenvalue 3: -4.02e-17
Eigenvector 4:
[[ 0.179 ]
[-0.3178]
[-0.3658]
[ 0.6011]]
Eigenvalue 4: -4.02e-17
5、通過減少特征值對特征向量進行排序,并選擇最上面的k。
通過減少特征值對特征對進行排序后,基于2個信息量最大的特征對構建d×k維度特征向量矩陣(稱之為W)。在下面的例子中,得到了下面的矩陣:
Matrix W:
[[-0.2049 -0.009 ]
[-0.3871 -0.589 ]
[ 0.5465 0.2543]
[ 0.7138 -0.767 ]]
6、使用矩陣W (4 × 2矩陣)通過方程將樣本轉換到新的子空間:Y = X*W,其中X是矩陣格式的原始數據(150 × 4矩陣),Y是轉換后的數據集(150 × 2矩陣)。
優點
最大化類分離:LDA的目的是最大限度地分離不同的類,使其有效的分類任務。
降維:與PCA一樣,LDA也可用于降維,其優點是考慮了類信息。
缺點
對異常值的敏感性:LDA對異常值非常敏感,異常值的存在會影響方法的性能。
正態性假設:LDA假設每個類中的特征是正態分布的,如果違反了這個假設,它可能無法很好地執行。
需要足夠的數據:LDA在每個類只有少量樣本的情況下可能表現不佳。擁有更多的樣本可以改善類參數的估計。
何時使用
分類任務:當目標是將數據分類到預定義的類中時,LDA是有益的。
保存類信息:當目標是在降低維數的同時保留與區分類相關的信息時,LDA非常有用
正態性假設成立:當類別內的正態分布假設成立時,LDA表現良好。
監督降維:當任務需要在類標簽的指導下進行降維時,LDA是一個合適的選擇。
Python代碼示例
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.datasets import make_classification
from sklearn.preprocessing import StandardScaler
# Generate a sample dataset
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
# Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Standardize the features (important for LDA)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# Initialize LDA and fit on the training data
lda = LinearDiscriminantAnalysis()
X_train_lda = lda.fit_transform(X_train, y_train)
# Calculate explained variance ratio for each component
explained_variance_ratio = lda.explained_variance_ratio_
# Calculate the cumulative explained variance
cumulative_explained_variance = np.cumsum(explained_variance_ratio)
# Find the number of components that explain at least 75% of the variance
n_components = np.argmax(cumulative_explained_variance >= 0.75) + 1
# Transform both the training and test data to the selected number of components
X_train_lda_selected = lda.transform(X_train)[:, :n_components]
X_test_lda_selected = lda.transform(X_test)[:, :n_components]
# Print the number of components selected
print(f"Number of components selected: {n_components}")
奇異值分解(SVD)
奇異值分解是一種矩陣分解技術,廣泛應用于線性代數、信號處理和機器學習等領域。它將一個矩陣分解成另外三個矩陣,原始矩陣以簡化形式表示。

SVD的工作步驟
1、矩陣分解
給定大小為M × n的矩陣M(或有M行n列的數據),奇異值分解將其分解為三個矩陣:M = u *Σ *v *
其中U是一個m × m正交矩陣,Σ是一個m × r對角矩陣,V是一個r × n正交矩陣。r是矩陣M的秩。
Σ的對角線元素為原矩陣M的奇異值,按降序排列。U的列是m的左奇異向量,這些向量構成了m的列空間的正交基,V的列是m的右奇異向量,這些向量構成了m的行空間的正交基。
2、簡化形式(Truncated SVD)
對于降維,通常使用截斷版本的奇異值分解。選擇Σ中前k個最大的奇異值。這些列可以從Σ中選擇,行可以從V 中選擇。由原矩陣M重構出一個新的矩陣B,公式如下:
B = u *Σ,B = V *A
其中Σ只包含原始Σ中奇異值的前k列,V包含原始V中奇異值對應的前k行。
優點
降維:SVD允許通過只保留最重要的奇異值和向量來降低維數。
數據壓縮:SVD用于數據壓縮任務,減少了矩陣的存儲需求。
降噪:通過只使用最顯著的奇異值,奇異值分解可以幫助減少數據中噪聲的影響。
數值穩定性:奇異值分解在數值上是穩定的,適合于求解病態系統中的線性方程。
正交性:SVD分解中的矩陣U和V是正交的,保留了原矩陣的行與列之間的關系。
推薦系統中的應用:奇異值分解廣泛應用于推薦系統的協同過濾。
缺點
計算復雜度:計算大型矩陣的完整SVD在計算上是非常昂貴的。
內存需求:存儲完整的矩陣U、Σ和V可能會占用大量內存,特別是對于大型矩陣。
對缺失值的敏感性:SVD對數據中的缺失值很敏感,處理缺失值需要專門的技術。
何時使用
降維:當目標是在保留數據基本結構的同時降低數據的維數時。
推薦系統:在基于協同過濾的推薦系統中,SVD用于識別捕獲用戶-物品交互的潛在因素。
數據壓縮:在需要壓縮或近似大型數據集的場景中。
信號處理:在信號處理中,采用奇異值分解進行降噪和特征提取。
主題建模:SVD被用于主題建模技術,如潛在語義分析(LSA)。
Python代碼示例
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.decomposition import TruncatedSVD
from sklearn.datasets import make_classification
from sklearn.preprocessing import StandardScaler
# Generate a sample dataset
X, y = make_classification(n_samples=1000, n_features=20, n_classes=2, random_state=42)
# Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Standardize the features (important for SVD)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# Initialize SVD and fit on the training data
svd = TruncatedSVD(n_components=X_train.shape[1] - 1) # Use one less component than the feature count
X_train_svd = svd.fit_transform(X_train)
# Calculate explained variance ratio for each component
explained_variance_ratio = svd.explained_variance_ratio_
# Calculate the cumulative explained variance
cumulative_explained_variance = np.cumsum(explained_variance_ratio)
# Find the number of components that explain at least 75% of the variance
n_components = np.argmax(cumulative_explained_variance >= 0.75) + 1
# Transform both the training and test data to the selected number of components
X_train_svd_selected = svd.transform(X_train)[:, :n_components]
X_test_svd_selected = svd.transform(X_test)[:, :n_components]
# Print the number of components selected
print(f"Number of components selected: {n_components}")
總結
在主成分分析(PCA)、線性判別分析(LDA)和奇異值分解(SVD)之間的選擇取決于數據的具體目標和特征。以下是關于何時使用每種技術的一般指導原則:
主成分分析:
- 當目標是降低數據集的維數時。
- 在捕獲數據中的全局模式和關系至關重要的場景中。
- 用于探索性數據分析和可視化。
線性判別分析:
- 在分類問題中,增強類之間的分離。
- 當有一個標記的數據集時,目標是找到一個最大化階級歧視的投影。
- 當正態分布類和等協方差矩陣的假設成立時,LDA特別有效。
奇異值分解:
- 當處理稀疏數據或缺失值時。
- 推薦系統的協同過濾。
- 奇異值分解也適用于數據壓縮和去噪。
三個技術的對比:
無監督vs有監督學習:PCA是無監督的,而LDA是有監督的。根據標記數據的可用性進行選擇。
類可分離性:如果目標是改進類可分離性,那么首選LDA。PCA和SVD關注的是總體方差。
數據特征:數據的特征,如線性、類別分布和異常值的存在,會影響選擇。
特定于應用程序的需求:考慮應用程序的特定需求,例如可解釋性、計算效率或對丟失數據的處理。
綜上所述,PCA適用于無監督降維,LDA適用于關注類可分性的監督問題,而SVD具有通用性,可用于包括協同過濾和矩陣分解在內的各種應用。
-
PCA
+關注
關注
0文章
91瀏覽量
30093 -
SVD
+關注
關注
0文章
21瀏覽量
12310 -
機器學習
+關注
關注
66文章
8497瀏覽量
134231 -
LDA
+關注
關注
0文章
29瀏覽量
10787 -
python
+關注
關注
56文章
4825瀏覽量
86374
發布評論請先 登錄

基于圖嵌入和最大互信息組合的降維
一種融入PCA的LBP特征降維車型識別算法
軟件架構設計的三個維度
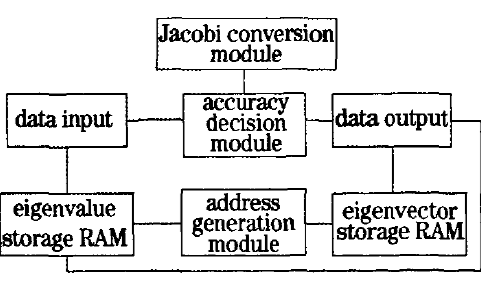
深入了解一下十大經典機器學習算法之一:PCA算法
基于Python查看SVD壓縮圖片的效果
如何使用FPGA實現高光譜圖像奇異值分解降維技術
元器件的三個降額等級資料下載






 三個主要降維技術對比介紹:PCA, LCA,SVD
三個主要降維技術對比介紹:PCA, LCA,SVD










評論