連續(xù)全通系統(tǒng)的零極點(diǎn)可以兩兩共軛對(duì)稱嗎?
連續(xù)全通系統(tǒng)的零極點(diǎn)可以兩兩共軛對(duì)稱。為了詳實(shí)地解釋這一觀點(diǎn),我將進(jìn)行詳細(xì)的闡述并提供背景知識(shí)和相關(guān)證明。
首先,讓我們了解什么是連續(xù)全通系統(tǒng)。連續(xù)全通系統(tǒng)是指由連續(xù)時(shí)間控制系統(tǒng)中的傳遞函數(shù)表示的系統(tǒng)。傳遞函數(shù)是輸入和輸出之間的數(shù)學(xué)關(guān)系,其中包含了系統(tǒng)的零點(diǎn)和極點(diǎn)。零點(diǎn)是傳遞函數(shù)等于0的輸入值,而極點(diǎn)是使傳遞函數(shù)趨近于無(wú)窮大的輸入值。
接下來(lái),讓我們來(lái)解釋兩兩共軛對(duì)稱的概念。在數(shù)學(xué)中,兩個(gè)數(shù)被稱為共軛對(duì)稱,當(dāng)且僅當(dāng)它們的虛部相等、實(shí)部互為相反數(shù)。這意味著如果我們有兩個(gè)共軛對(duì)稱的極點(diǎn),它們具有相同的虛部但實(shí)部互為相反數(shù)。
我們將說(shuō)明連續(xù)全通系統(tǒng)的零極點(diǎn)可以兩兩共軛對(duì)稱。為此,我們需要使用復(fù)數(shù)和復(fù)變函數(shù)理論。
首先,假設(shè)我們有一個(gè)連續(xù)全通系統(tǒng)的傳遞函數(shù)H(s)。這個(gè)傳遞函數(shù)可以寫成以下形式:
H(s) = (s - z1)(s - z2)(s - z3)...(s - zn) / (s - p1)(s - p2)(s - p3)...(s - pn)
其中zi是系統(tǒng)的零點(diǎn),pi是系統(tǒng)的極點(diǎn)。
現(xiàn)在,讓我們假設(shè)我們有一對(duì)共軛對(duì)稱的零點(diǎn)z1和z2,這意味著它們的虛部相等,且實(shí)部互為相反數(shù)。也可以表示為z1 = a + bi,z2 = a - bi,其中a和b是實(shí)數(shù),b≠0。
我們可以通過(guò)將這兩個(gè)零點(diǎn)相乘來(lái)表示它們的乘積:
z1 * z2 = (a + bi)(a - bi) = a^2 + b^2
這個(gè)結(jié)果是一個(gè)實(shí)數(shù),沒(méi)有虛部。這意味著z1 * z2是傳遞函數(shù)的一部分,但它不會(huì)引入額外的復(fù)雜度。類似地,對(duì)于其他共軛對(duì)稱的零點(diǎn)對(duì)也是如此。
現(xiàn)在,讓我們看看連續(xù)全通系統(tǒng)的極點(diǎn)是否也可以共軛對(duì)稱。我們假設(shè)我們有一對(duì)共軛對(duì)稱的極點(diǎn)p1和p2,這意味著它們的虛部相等,且實(shí)部互為相反數(shù)。同樣可以表示為p1 = c + di,p2 = c - di,其中c和d是實(shí)數(shù),d≠0。
我們可以通過(guò)將這兩個(gè)極點(diǎn)相乘來(lái)表示它們的乘積:
p1 * p2 = (c + di)(c - di) = c^2 + d^2
這個(gè)結(jié)果是一個(gè)實(shí)數(shù),沒(méi)有虛部。這意味著p1 * p2是傳遞函數(shù)的一部分,但它不會(huì)引入額外的復(fù)雜度。類似地,對(duì)于其他共軛對(duì)稱的極點(diǎn)對(duì)也是如此。
綜上所述,連續(xù)全通系統(tǒng)的零極點(diǎn)可以兩兩共軛對(duì)稱。無(wú)論是零點(diǎn)還是極點(diǎn),它們的共軛對(duì)稱性都不會(huì)增加系統(tǒng)的復(fù)雜度。
最后,我想強(qiáng)調(diào)一點(diǎn),對(duì)于連續(xù)全通系統(tǒng)來(lái)說(shuō),共軛對(duì)稱的零極點(diǎn)是一種較為簡(jiǎn)潔和優(yōu)美的表示方式。通過(guò)使用共軛對(duì)稱的零極點(diǎn),我們可以更方便地分析和設(shè)計(jì)連續(xù)全通系統(tǒng),使其性能更加可控和穩(wěn)定。
希望本文能夠詳實(shí)地解答你的問(wèn)題,并提供了足夠的背景知識(shí)和證明來(lái)支持這一觀點(diǎn)。如果你有任何其他疑問(wèn),請(qǐng)隨時(shí)提問(wèn)。
-
傳遞函數(shù)
+關(guān)注
關(guān)注
0文章
103瀏覽量
14245
發(fā)布評(píng)論請(qǐng)先 登錄
零極點(diǎn)仿真分析簡(jiǎn)介
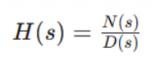
OCAD應(yīng)用:四組元連續(xù)變焦系統(tǒng)
開(kāi)關(guān)電源環(huán)路穩(wěn)定性分析——觀察法找零極點(diǎn)
雙面電極點(diǎn)焊電源技術(shù)研究與應(yīng)用實(shí)踐






 連續(xù)全通系統(tǒng)的零極點(diǎn)可以兩兩共軛對(duì)稱嗎?
連續(xù)全通系統(tǒng)的零極點(diǎn)可以兩兩共軛對(duì)稱嗎?











評(píng)論