1. 振蕩器原理
1.1 振蕩條件
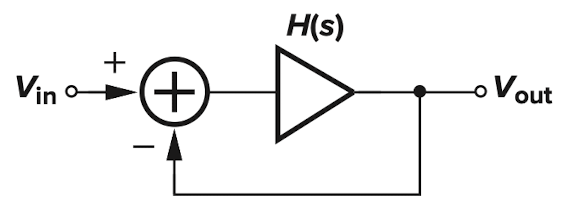
圖一
對圖一這樣的閉環系統,要想實現振蕩,最基本的就是要滿足不穩定的條件,也就是巴克豪森準則:

其中ω0即為振蕩頻率。也就是說,在整個環路相移360°時幅值不小于1。

圖二
假設H(s)為單極點系統,如圖二。由于系統在DC情況下是負反饋,默認有180°相移,而單個極點最多貢獻90°相移,加起來一共270°,達不到前面要求的360°,因而無法振蕩。那么,假設我們串聯兩級作為H(s),如圖三,會發現兩個極點最多貢獻180°,而現在在DC是正反饋,沒有默認的相移,因此也無法達到360°,所以無法振蕩。事實上,環形振蕩器至少需要3個極點,如圖四,三個極點一共可以貢獻270°,加上負反饋的180°,足以達到振蕩條件。

圖三

圖四
除了相位條件以外,還要滿足相應的幅值條件。假設每一級極點相同,均為ω0,將圖四的環路增益表達如下:

振蕩時總相移360°,除了本身的負反饋180°以外,每一級貢獻60°。可以計算得振蕩頻率ωosc和ω0的關系:


此時要求環路增益至少為1,可以求得對每一級低頻增益的要求:


因此,每一級低頻增益至少為2。
1.2 小信號與大信號
前面說了A0=2是保證振蕩的基本條件,那么如果A0>2呢?為了方便理解,我們將圖四的閉環傳遞函數推導如下:


有一個左半平面的閉環實極點,一對復極點。容易看出,A0=2時,這一對復極點位于虛軸上,處于臨界穩定態;A0>2時,復極點位于右半平面,系統不穩定。這兩種情況都可以保證振蕩。忽略s1的影響,可以將時域表達式推導出來:

因此,A0>2時,指數項隨時間增長而上升,最終趨于正無窮。這也說明系統是發散的,不穩定的。
事實上,由于電路的供電是一定的,振蕩器的輸出信號不可能真的到正無窮,最多只會飽和到電源電壓。此時已經脫離了小信號的范疇,從大信號的角度分析,假設每級延時為TD,三級振蕩器的振蕩周期為6TD,頻率為1/6TD。容易發現,這和前面的表達式里的頻率A0*√3/2不同,一般會比它更低。

圖五
怎么去理解這件事呢?如圖五,假設一開始每級輸出節點都處于中間電平,引入一點噪聲之后每個節點開始逐漸振蕩。一開始的幅度比較小,認為是小信號,振蕩頻率是A0*√3/2。隨著幅度增長,電路逐漸脫離線性系統的范疇,振蕩頻率更接近大信號分析的1/6TD。最終振蕩頻率為1/6TD。
2. 電路實現
根據文章,早在1953年的真空管時代,一位叫Galley的前輩就提出了一個九級的環形振蕩器專利,每一級本質上就是一個反相器。這種基于反相器的結構如圖六。

圖六
如前面所說,一共N級的話,振蕩頻率為1/(2NTD)。
除此之外,也可以用全差分的方式實現,如圖七。

圖七
由于篇幅所限,兩種電路的具體分析與對比就留到下次再補充了。
-
振蕩器
+關注
關注
28文章
3974瀏覽量
140539 -
小信號
+關注
關注
1文章
52瀏覽量
12362 -
大信號
+關注
關注
0文章
9瀏覽量
7565
發布評論請先 登錄
一文詳解振蕩器
振蕩器,振蕩器的分類,振蕩器的特性
振蕩器,振蕩器的分類和原理是什么?
壓控振蕩器,壓控振蕩器是什么意思
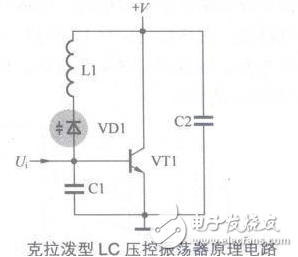
壓控振蕩器電路圖大全(八款壓控振蕩器電路設計原理圖詳解)





 振蕩器原理詳解(1)
振蕩器原理詳解(1)










評論