低通濾波器電路是一種能夠通過濾除高頻信號而通過低頻信號的電路。它廣泛應用于信號處理、音頻放大和通信系統中,用于去除噪音和不需要的高頻成分。低通濾波器的設計和傳遞函數計算是相關電子學和信號處理課程中的重要內容。下面,我將詳細介紹低通濾波器的電路特點及傳遞函數的計算方法。
首先,我們來了解一下低通濾波器的電路特點。
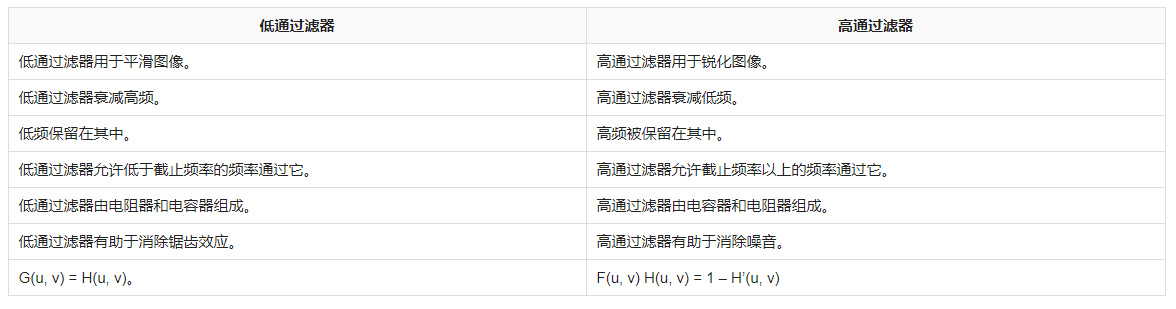
- 頻率響應:低通濾波器具有截止頻率,高于截止頻率的信號會被濾除,而低于截止頻率的信號會通過。這意味著低通濾波器可以去除高頻成分,僅保留低頻成分。
- 幅頻特性:低通濾波器在通過低頻信號時幅度基本保持不變,而隨著頻率的增加,幅度逐漸下降。這種幅頻特性使得低通濾波器可以用于音頻放大器中,使音頻信號放大時不會產生失真。
- 相頻特性:低通濾波器會引入相位延遲,隨著頻率的增加,相位延遲會逐漸增加。這對于某些特定應用,如音頻信號處理和通信系統是非常重要的。
- 階數:低通濾波器的階數決定了其頻率選擇性能和幅度下降速度。階數越高,濾波器的選擇性和幅度下降速度越大。
接下來,我們將介紹低通濾波器傳遞函數的計算方法。
傳遞函數是指輸入信號和輸出信號之間的數學關系,用于描述濾波器的工作原理。在信號處理中,傳遞函數通常以頻域表達,也稱作頻域傳輸特性。
低通濾波器的傳遞函數可以用各種方式表示,包括巴特沃斯(Butterworth)、切比雪夫(Chebyshev)、橢圓(Elliptic)等。下面,我們以巴特沃斯濾波器為例,介紹傳遞函數的計算方法。
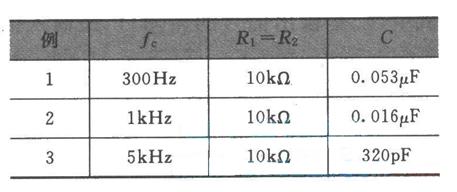
巴特沃斯濾波器是一種優化了幅度特性和相頻特性的低通濾波器。其傳遞函數公式為:
H(s) = 1 / (1 + (s/Wc)^2N)^0.5
其中,H(s)為傳遞函數,s為復頻率變量,Wc為截止頻率,N為濾波器的階數。
傳遞函數中的復頻率變量s可以表示為s = jω,其中j為虛數單位,ω為角頻率。將s替換為jω,并對傳遞函數進行數學運算,最終可以得到傳遞函數的頻域表達式。
通過計算傳遞函數的頻域表達式,可以獲得低通濾波器在不同頻率下的增益和相位特性。這些特性可以用來分析和設計低通濾波器,以滿足特定應用的要求。
除了巴特沃斯濾波器,切比雪夫和橢圓濾波器也有相應的傳遞函數表達式,具體計算方法類似,但是形式略有不同。針對不同的應用場景和性能需求,可以選擇合適的濾波器類型和相應的傳遞函數表達式進行設計。
總結起來,低通濾波器是一種能夠通過濾除高頻信號而通過低頻信號的電路,具有頻率響應、幅頻特性、相頻特性和階數等特點。傳遞函數是用于描述濾波器輸入輸出關系的數學表達式,可以通過不同濾波器類型的特定公式來計算。
-
低通濾波器
+關注
關注
14文章
485瀏覽量
47535 -
通信系統
+關注
關注
6文章
1204瀏覽量
53460 -
函數
+關注
關注
3文章
4346瀏覽量
62973 -
低頻信號
+關注
關注
2文章
49瀏覽量
8344
發布評論請先 登錄
相關推薦
無源低通濾波器電路,有源低通濾波器原理圖
四種低通濾波器的電路分析
低通濾波器傳遞函數
LC低通濾波器作用及應用案例
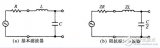
低通濾波器的設計與實現
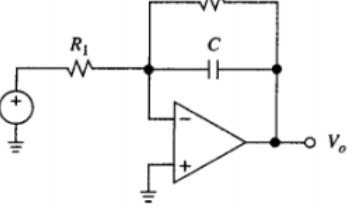
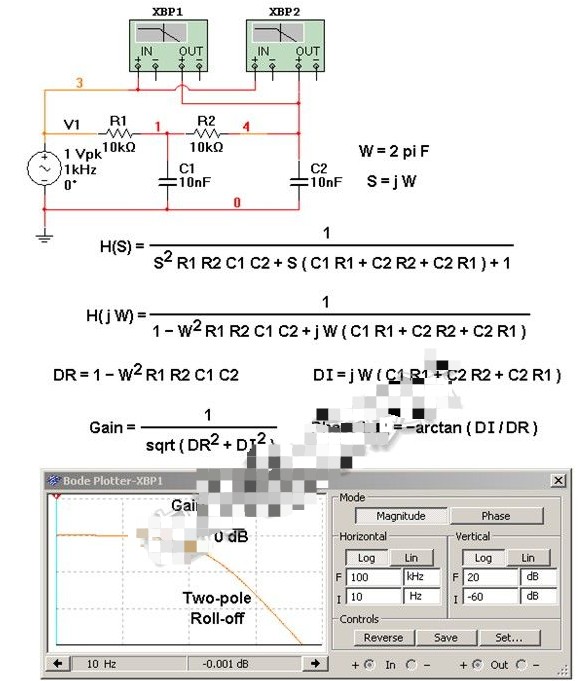
基于使用雙極點RC低通濾波器推導代數傳遞函數
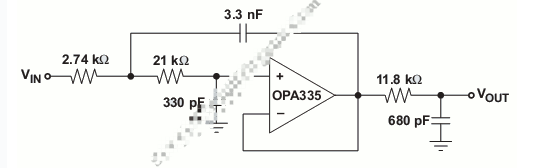
低通濾波器電路圖分享




 低通濾波器電路特點 低通濾波器傳遞函數怎么算
低通濾波器電路特點 低通濾波器傳遞函數怎么算

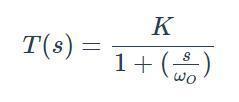











評論