拉格朗日乘子法無(wú)疑是最優(yōu)化理論中最重要的一個(gè)方法。但是現(xiàn)在網(wǎng)上并沒(méi)有很好的完整介紹整個(gè)方法的文章。所以小編整理了如下文章,希望能博得大家一贊。
在求取有約束條件的優(yōu)化問(wèn)題時(shí),拉格朗日乘子法(Lagrange Multiplier) 和KKT條件是非常重要的兩個(gè)求取方法,對(duì)于等式約束的優(yōu)化問(wèn)題,可以應(yīng)用拉格朗日乘子法去求取最優(yōu)值;如果含有不等式約束,可以應(yīng)用KKT條件去求取。當(dāng)然,這兩個(gè)方法求得的結(jié)果只是必要條件,只有當(dāng)是凸函數(shù)的情況下,才能保證是充分必要條件。
KKT條件是拉格朗日乘子法的泛化。之前學(xué)習(xí)的時(shí)候,只知道直接應(yīng)用兩個(gè)方法,但是卻不知道為什么拉格朗日乘子法(Lagrange Multiplier) 和KKT條件能夠起作用,為什么要這樣去求取最優(yōu)值呢?本文將首先把什么是拉格朗日乘子法(Lagrange Multiplier) 和KKT條件敘述一下;然后開始分別談?wù)劄槭裁匆@樣求最優(yōu)值。
一.拉格朗日乘子法(Lagrange Multiplier) 和KKT條件通常我們需要求解的最優(yōu)化問(wèn)題有如下幾類
:(i) 無(wú)約束優(yōu)化問(wèn)題,可以寫為:min f(x); (ii) 有等式約束的優(yōu)化問(wèn)題,可以寫為:min f(x),s.t. h_i(x) = 0; i =1, ..., n(iii) 有不等式約束的優(yōu)化問(wèn)題,可以寫為:min f(x),s.t. g_i(x) <= 0; i =1, ..., nh_j(x) = 0; j =1, ..., m對(duì)于第(i)類的優(yōu)化問(wèn)題,常常使用的方法就是Fermat定理,即使用求取f(x)的導(dǎo)數(shù),然后令其為零,可以求得候選最優(yōu)值,再在這些候選值中驗(yàn)證;如果是凸函數(shù),可以保證是最優(yōu)解。對(duì)于第(ii)類的優(yōu)化問(wèn)題,常常使用的方法就是拉格朗日乘子法(Lagrange Multiplier) ,即把等式約束h_i(x)用一個(gè)系數(shù)與f(x)寫為一個(gè)式子,稱為拉格朗日函數(shù),而系數(shù)稱為拉格朗日乘子。通過(guò)拉格朗日函數(shù)對(duì)各個(gè)變量求導(dǎo),令其為零,可以求得候選值集合,然后驗(yàn)證求得最優(yōu)值。
對(duì)于第(iii)類的優(yōu)化問(wèn)題,常常使用的方法就是KKT條件。同樣地,我們把所有的等式、不等式約束與f(x)寫為一個(gè)式子,也叫拉格朗日函數(shù),系數(shù)也稱拉格朗日乘子,通過(guò)一些條件,可以求出最優(yōu)值的必要條件,這個(gè)條件稱為KKT條件。
(a)拉格朗日乘子法(Lagrange Multiplier)對(duì)于等式約束,我們可以通過(guò)一個(gè)拉格朗日系數(shù)a 把等式約束和目標(biāo)函數(shù)組合成為一個(gè)式子L(a, x) = f(x) + a*h(x), 這里把a(bǔ)和h(x)視為向量形式,a是橫向量,h(x)為列向量,之所以這么寫,完全是因?yàn)閏sdn很難寫數(shù)學(xué)公式,只能將就了.....。然后求取最優(yōu)值,可以通過(guò)對(duì)L(a,x)對(duì)各個(gè)參數(shù)求導(dǎo)取零,聯(lián)立等式進(jìn)行求取,這個(gè)在高等數(shù)學(xué)里面有講,但是沒(méi)有講為什么這么做就可以,在后面,將簡(jiǎn)要介紹其思想。(b)KKT條件對(duì)于含有不等式約束的優(yōu)化問(wèn)題,如何求取最優(yōu)值呢?常用的方法是KKT條件,同樣地,把所有的不等式約束、等式約束和目標(biāo)函數(shù)全部寫為一個(gè)式子L(a, b, x)= f(x) + a*g(x)+b*h(x),KKT條件是說(shuō)最優(yōu)值必須滿足以下條件:
1. L(a, b, x)對(duì)x求導(dǎo)為零;2. h(x) =0;3. a*g(x) = 0;求取這三個(gè)等式之后就能得到候選最優(yōu)值。其中第三個(gè)式子非常有趣,因?yàn)間(x)<=0,如果要滿足這個(gè)等式,必須a=0或者g(x)=0. 這是SVM的很多重要性質(zhì)的來(lái)源,如支持向量的概念。
二. 為什么拉格朗日乘子法(Lagrange Multiplier) 和KKT條件能夠得到最優(yōu)值?
為什么要這么求能得到最優(yōu)值?先說(shuō)拉格朗日乘子法,設(shè)想我們的目標(biāo)函數(shù)z = f(x), x是向量, z取不同的值,相當(dāng)于可以投影在x構(gòu)成的平面(曲面)上,即成為等高線,如下圖,目標(biāo)函數(shù)是f(x, y),這里x是標(biāo)量,虛線是等高線,現(xiàn)在假設(shè)我們的約束g(x)=0,x是向量,在x構(gòu)成的平面或者曲面上是一條曲線,假設(shè)g(x)與等高線相交,交點(diǎn)就是同時(shí)滿足等式約束條件和目標(biāo)函數(shù)的可行域的值,但肯定不是最優(yōu)值,因?yàn)橄嘟灰馕吨隙ㄟ€存在其它的等高線在該條等高線的內(nèi)部或者外部,使得新的等高線與目標(biāo)函數(shù)的交點(diǎn)的值更大或者更小,只有到等高線與目標(biāo)函數(shù)的曲線相切的時(shí)候,可能取得最優(yōu)值,如下圖所示,即等高線和目標(biāo)函數(shù)的曲線在該點(diǎn)的法向量必須有相同方向,所以最優(yōu)值必須滿足:f(x)的梯度 = a* g(x)的梯度,a是常數(shù),表示左右兩邊同向。這個(gè)等式就是L(a,x)對(duì)參數(shù)求導(dǎo)的結(jié)果。

而KKT條件是滿足強(qiáng)對(duì)偶條件的優(yōu)化問(wèn)題的必要條件,可以這樣理解:我們要求min f(x), L(a, b, x) = f(x) + a*g(x) + b*h(x),a>=0,我們可以把f(x)寫為:max_{a,b} L(a,b,x),為什么呢?因?yàn)閔(x)=0, g(x)<=0,現(xiàn)在是取L(a,b,x)的最大值,a*g(x)是<=0,所以L(a,b,x)只有在a*g(x) = 0的情況下才能取得最大值,否則,就不滿足約束條件,因此max_{a,b} L(a,b,x)在滿足約束條件的情況下就是f(x),因此我們的目標(biāo)函數(shù)可以寫為 min_x max_{a,b} L(a,b,x)。如果用對(duì)偶表達(dá)式:?max_{a,b}?min_x ?L(a,b,x),由于我們的優(yōu)化是滿足強(qiáng)對(duì)偶的(強(qiáng)對(duì)偶就是說(shuō)對(duì)偶式子的最優(yōu)值是等于原問(wèn)題的最優(yōu)值的),所以在取得最優(yōu)值x0的條件下,它滿足 f(x0) =?max_{a,b}?min_x ?L(a,b,x) =?min_x max_{a,b} L(a,b,x) =f(x0),我們來(lái)看看中間兩個(gè)式子發(fā)生了什么事情:
f(x0) =max_{a,b}min_x L(a,b,x) =max_{a,b}min_x f(x) + a*g(x) + b*h(x) =max_{a,b} f(x0)+a*g(x0)+b*h(x0)= f(x0)
可以看到上述加黑的地方本質(zhì)上是說(shuō)min_xf(x) + a*g(x) + b*h(x) 在x0取得了最小值,用fermat定理,即是說(shuō)對(duì)于函數(shù)f(x) + a*g(x) + b*h(x),求取導(dǎo)數(shù)要等于零,即f(x)的梯度+a*g(x)的梯度+ b*h(x)的梯度 = 0
這就是kkt條件中第一個(gè)條件:L(a, b, x)對(duì)x求導(dǎo)為零。
而之前說(shuō)明過(guò),a*g(x) = 0,這時(shí)kkt條件的第3個(gè)條件,當(dāng)然已知的條件h(x)=0必須被滿足,所有上述說(shuō)明,滿足強(qiáng)對(duì)偶條件的優(yōu)化問(wèn)題的最優(yōu)值都必須滿足KKT條件,即上述說(shuō)明的三個(gè)條件。可以把KKT條件視為是拉格朗日乘子法的泛化。
-
機(jī)器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8499瀏覽量
134331
原文標(biāo)題:機(jī)器學(xué)習(xí)基礎(chǔ) 深入理解拉格朗日乘子法
文章出處:【微信號(hào):weixin21ic,微信公眾號(hào):21ic電子網(wǎng)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
機(jī)器學(xué)習(xí)基礎(chǔ)|深入理解拉格朗日乘子法
條件編譯是先判斷變量是否被宏定義嗎
如何利用文件名來(lái)定義case結(jié)構(gòu)的條件
基于預(yù)條件共軛梯度法的混凝土層析成像
如何搞定機(jī)器學(xué)習(xí)中的拉格朗日?看看這個(gè)乘子法與KKT條件大招
基于KKT和SVM算法的云架構(gòu)入侵檢測(cè)系統(tǒng)
區(qū)間聯(lián)絡(luò)線選取方法

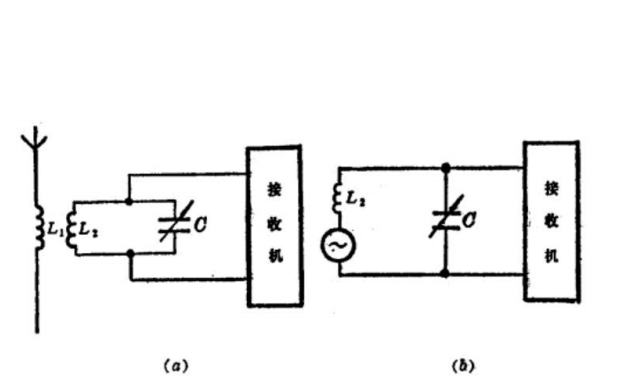
串聯(lián)諧振電路的定義條件和特點(diǎn)及應(yīng)用與選擇說(shuō)明
機(jī)器學(xué)習(xí)筆記之優(yōu)化-拉格朗日乘子法和對(duì)偶分解
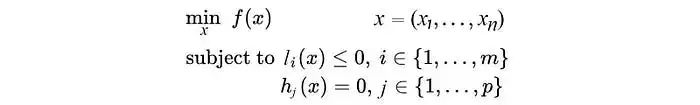





 拉格朗日乘子法和KKT條件的定義及選取原因
拉格朗日乘子法和KKT條件的定義及選取原因











評(píng)論