主要內(nèi)容：

為什么梯度的負(fù)方向是局部下降最快的方向？

剛接觸梯度下降這個概念的時候，是在學(xué)習(xí)機器學(xué)習(xí)算法的時候，很多訓(xùn)練算法用的就是梯度下降，然后資料和老師們也說朝著梯度的反方向變動，函數(shù)值下降最快，但是究其原因的時候，很多人都表達(dá)不清楚。所以我整理出自己的理解，從方向?qū)?shù)這個角度把這個結(jié)論證明出來，讓我們知其然也知其所以然~

這次從最優(yōu)化的角度切入來說明一下：

當(dāng)我們在某個要優(yōu)化的函數(shù)，這里設(shè)為f(x),我們在x點處，然后沿方向 v進(jìn)行移動，到達(dá)f(x+v)，圖示表示了移動過程：

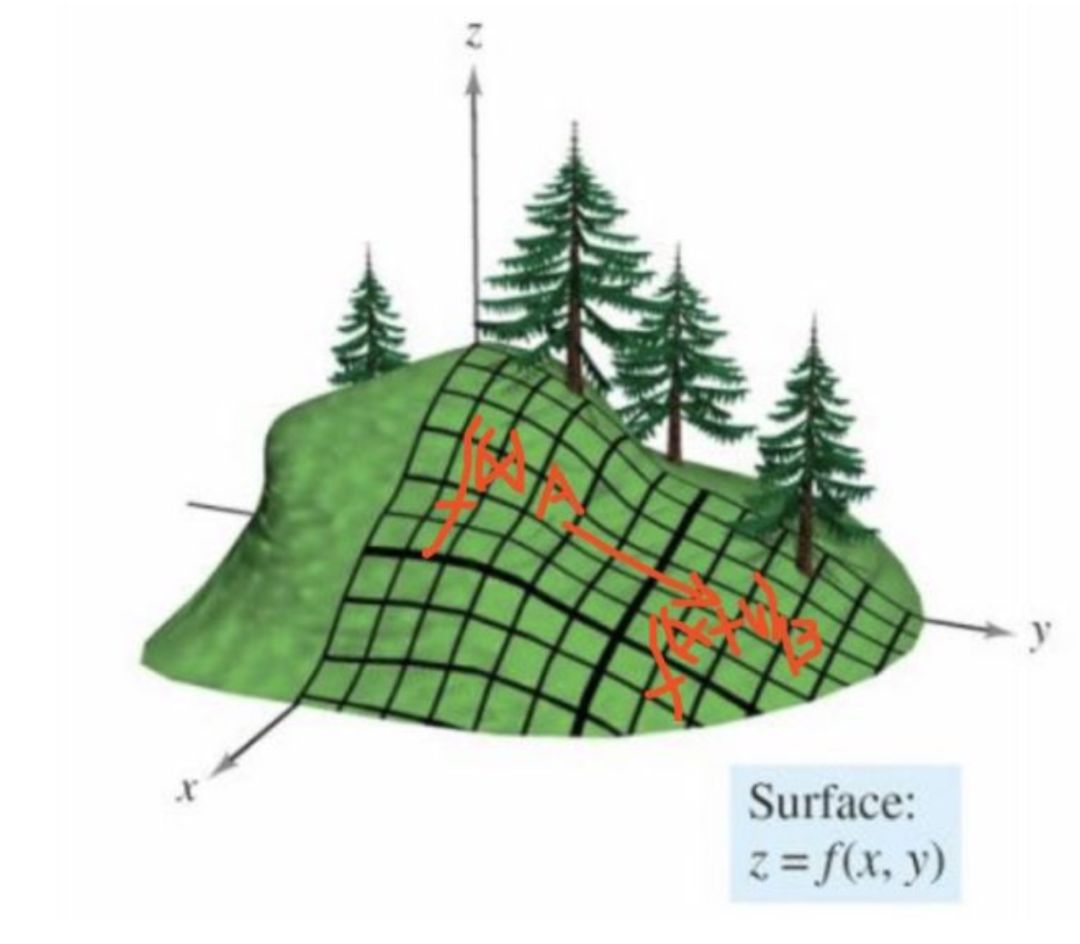
上圖顯示了從A點,移動到B點的過程。那么 v方向是什么的時候，局部下降的最快呢？

換成數(shù)學(xué)語言來說就是， f(x+v)-f(x)的值在 v是什么的時候，達(dá)到最大！

下面進(jìn)行講解：

則 f(x+v)-f(x)=d f(x)v ,則我們可以得出： d f(x)v 為函數(shù)值的變化量，我們要注意的是 d f(x) 和 v 均為向量， d f(x)v 也就是兩個向量進(jìn)行點積，而向量進(jìn)行點積的最大值，也就是兩者共線的時候，也就是說 v 的方向和 d f(x) 方向相同的時候，點積值最大，這個點積值也代表了從A點到B點的上升量。點積說明如下：

而 df(x)正是代表函數(shù)值在x處的梯度。前面又說明了v的方向和df(x)方向相同的時候，點積值（變化值）最大，所以說明了梯度方向是函數(shù)局部上升最快的方向。也就證明了梯度的負(fù)方向是局部下降最快的方向！