在現(xiàn)代通信和信號處理領(lǐng)域,傅里葉變換(FT)扮演著核心角色。它不僅幫助我們分析信號的頻率成分,還能用于濾波、壓縮和信號恢復(fù)等多種任務(wù)。
傅里葉變換的基本原理
傅里葉變換是一種將信號從時域轉(zhuǎn)換到頻域的數(shù)學(xué)方法。它基于傅里葉級數(shù)的概念,即任何周期函數(shù)都可以表示為正弦和余弦函數(shù)的和。對于非周期信號,傅里葉變換提供了一種將信號分解為不同頻率成分的方法。
應(yīng)用1:頻譜分析
頻譜分析是傅里葉變換最直接的應(yīng)用之一。通過傅里葉變換,我們可以將時間域中的信號轉(zhuǎn)換為頻率域中的頻譜,從而分析信號的頻率成分。這對于識別信號中的周期性成分、噪聲水平和信號的帶寬等特性至關(guān)重要。
應(yīng)用2:濾波
濾波是信號處理中的一個重要環(huán)節(jié),用于去除不需要的頻率成分或保留特定的頻率范圍。傅里葉變換使得濾波操作變得簡單,因為我們可以設(shè)計濾波器的頻率響應(yīng),然后通過傅里葉變換將其應(yīng)用于信號。
應(yīng)用3:信號壓縮
信號壓縮技術(shù)旨在減少信號的存儲或傳輸所需的數(shù)據(jù)量。傅里葉變換在信號壓縮中扮演著重要角色,尤其是在小波變換和離散余弦變換(DCT)等壓縮算法中。通過傅里葉變換,我們可以識別信號中的重要頻率成分,并僅保留這些成分以實現(xiàn)壓縮。
應(yīng)用4:信號恢復(fù)
在信號傳輸過程中,信號可能會受到干擾或失真。傅里葉變換可以幫助我們識別和補(bǔ)償這些失真。通過分析信號的頻譜,我們可以設(shè)計濾波器來消除或減少干擾,從而恢復(fù)信號的原始特性。
應(yīng)用5:圖像處理
傅里葉變換在圖像處理領(lǐng)域也有廣泛應(yīng)用,如圖像去噪、邊緣檢測和圖像壓縮等。通過將圖像轉(zhuǎn)換到頻率域,我們可以更容易地識別和處理圖像中的不同特征。
應(yīng)用6:語音處理
在語音處理中,傅里葉變換用于語音信號的分析和合成。通過傅里葉變換,我們可以提取語音信號的頻譜特征,用于語音識別、語音合成和語音編碼等應(yīng)用。
結(jié)論
傅里葉變換是信號處理領(lǐng)域的一項基礎(chǔ)技術(shù),它在頻譜分析、濾波、壓縮、信號恢復(fù)等多個方面都有著廣泛的應(yīng)用。隨著技術(shù)的發(fā)展,傅里葉變換的應(yīng)用領(lǐng)域還在不斷擴(kuò)展,對于提高信號處理的效率和質(zhì)量起著至關(guān)重要的作用。
-
信號處理
+關(guān)注
關(guān)注
48文章
1052瀏覽量
103749 -
頻率
+關(guān)注
關(guān)注
4文章
1551瀏覽量
59819 -
頻譜
+關(guān)注
關(guān)注
7文章
891瀏覽量
46166 -
傅里葉變換
+關(guān)注
關(guān)注
6文章
442瀏覽量
42909
發(fā)布評論請先 登錄
相關(guān)推薦
傅里葉變換和拉普拉斯變換有什么區(qū)別
小波變換思想及其在信號處理中的應(yīng)用
非周期信號的傅里葉變換
傅里葉變換與小波變換在信號去噪中的應(yīng)用
傅里葉變換的介紹傅里葉變換有什么意義和應(yīng)用






 傅里葉變換在信號處理中的應(yīng)用
傅里葉變換在信號處理中的應(yīng)用
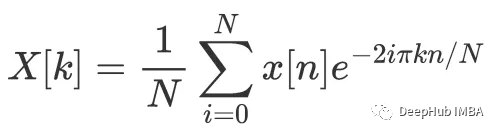










評論