本文針對航空發動機的轉子/整機動力學問題，使用兩自由度動力學模型對轉、靜子的振動耦合機理進行了解釋，指出傳統轉子動力學模型將導致最大67%的計算誤差，因此需要采用整機動力學模型對發 動機的振動特性進行求解。進一步明確了整機動力學有限元模型的簡化原則和模型功用，針對轉、靜子的 典型結構論述了詳細的建模方法。采用整機三維模型對雙轉子渦扇發動機的固有振動特性進行了計算和評估，結果表明，慢車至最大轉速區間內只存在一階高壓轉子平動振型，轉子系統總應變能不超過20%，共 振裕度大于20%，滿足航空發動機的轉子動力學設計要求。

與地面燃氣輪機相比，現代航空發動機的一個典型特點是轉子系統與靜子系統的剛度接近，因而轉靜子之間的振動耦合問題突出。不能夠準確合理的考慮靜子剛度、質量特征對轉子振動特性的影響，將帶來轉子臨界轉速、不平衡響應等計算結果的較大誤差。雖然可以采用支承動剛度對此問題進行近似考慮，但臨界轉速附近的振動響應求解不準確， 同時無論采用測試方法還是數值仿真計算，都很難 獲得真實發動機各支點的動剛度值。

為避免上述問題，航空發動機設計中可采用梁單元對渦扇發動機建立整機動力學分析模型，其中機匣被等效為零轉速的轉子 。陳果，Philip利用梁單元建立了整機動力學模型，并計入了滾動軸承和擠壓油膜阻尼器的非線性，獲得了整機模態特征。但基于梁單元的有限元模型卻存在如下局限性：①高壓壓氣機的大直徑鼓筒并不滿足長徑比足夠大的梁單元假設，會帶來彎曲模態頻率求解誤差偏大；②不能精確刻劃轉子中錐形殼體的質量和剛度沿軸向的變化；③不能考慮離心預應力的剛度增 強效應。因此近年來國外均發展了整機的三維動力學模型建立與分析方法。Romuald采用三維殼單元整機模型對 EJ200渦扇發動機的振動響應等問題進行了計算，并與臺架試車結果進行了對比。Jose， Garcia針對航空發動機的建模方法進行了系統的研究，并采用整機三維殼體模型對其在沖擊載荷下的振動響應特征進行了分析。

本文使用兩自由度動力學模型對航空發動機中轉、靜子的振動耦合機理進行解釋，并給出整機動力學模型的建立方法和功用，最后通過算例給出順轉 雙轉子發動機的臨界轉速確定方法。

1 轉靜子振動耦合機理

航空發動機系統由于轉子系統的剛度、質量與靜子系統相接近，因此需要采用整機模型對其振動特性進行求解，否則將帶來不可接受的誤差。對于此誤差的產生機理，可使用如下力學模型給予類別分析和說明。

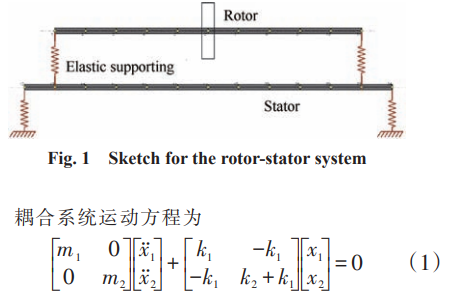
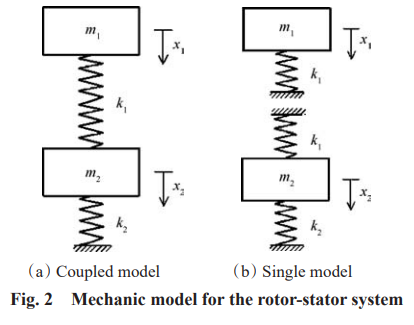
轉子軸系通過彈性支承與靜子系統相連接，如圖1所示。其對應力學模型如圖2所示，圖中m1為轉子軸系總質量；k1為彈性支承的剛度；m2為靜子系統質量；k2為靜子系統剛度。其中圖 2（a）為耦合模型， 對應于整機動力學模型；圖 2（b）為獨立模型，對應于傳統的轉子動力學模型。

通過頻率特征方程，可得特征值（即固有頻率）為

由于式（2）（3）的結果不夠直觀，下面對兩種假設情況進行對比。

對于地面旋轉機械 k2>> k1,m2>> m1，可假設 k2=100k1，m2=m1，則有式（4），可見對于轉子的固有頻率 ω1 ，采用兩種模型獲得的結果相差很小，相對誤差為 5%。

由上述分析可知，只有使用整機動力學模型，才可以準確地獲得航空發動機轉子系統的固有頻率， 才可以進一步準確地求解轉子系統臨界轉速。

2 整機動力學有限元模型建立方法

2.1 模型簡化的必要性與基本原則

采用實體單元模型可以更為準確地描述航空發動機轉靜子系統的復雜結構特征，但必須進行適當合理的等效簡化。其一是由于發動機結構復雜，如果過于考慮圓角、小孔等細節因素，將導致所建立的模型自由度過多，計算經濟性差，甚至無法完成計算。其二是由于目前的有限元軟件中固有模態求解模塊是無法對局部振動和整體振動進行區分的，因而會導致計算結果中局部模態過于豐富，使轉子/整機振動模態被盤片耦合等局部振動模態所湮沒， 很難完成關心模態的提取工作。

因此，在整機動力學模型建立中，必須大幅度的簡化以控制模型的自由度數。為保證動力學特征的準確性，應重點保證模型質量、剛度與實際結構的相 似性 。具體而言，①應保證模型的質量分布與實際結構相似，尤其是質量沿軸向的分布特征、重心位置；②應保證轉動慣量的分布與實際結構相似，尤其 是轉子軸系的轉動慣量的軸向分布特征；③抗彎剛度的分布相似。

2.2 整機動力學模型的功用

整機動力學有限元模型并非適用于所有的強度、振動問題，追求功用過多只會導致模型自由度過大，無法完成計算。本文方法所建立的模型重點在于實現如下功用：

①可以準確考慮轉/靜子之間的振動耦合，獲得更為準確的轉子臨界轉速以及發動機整機振動特性。

②可為部件計算提供準確的邊界條件。整機動力學模型不能考慮圓角、小孔等局部細節對應力分布的影響，本身并不 適用于靜強度分析。但根據子模型原理，可以根據其計算獲得的位移分布為部件計算提供準確的邊界條件定義。

③用于分析因振動引起的轉靜子間隙變化。

④為安裝節設計與飛發協調設計提供準確的等效模型和載荷條件。在飛機總體設計中是將發動機作為質量塊和激勵參數處理的，應用整機模型可以計算得到各種工況下的外傳力大小及頻率特征，提供準確的飛發載荷。

⑤可用于計算發動機轉/靜子軸向力，獲得機匣載荷的準確分布特征，為發動機總體結構中傳力路線的設計提供技術支撐。

下面以 ANSYS 通用有限元程序為例，對航空發動機典型結構建模方法進行詳細論述。

2.3 轉子典型結構建模方法

（1）轉子葉盤結構

葉盤結構是航空發動機轉子軸系的主要部件， 一些文獻在葉片處理上，將其直接等效為集中質量單元，而輪盤使用實體單元，由于不同單元類型的節 點自由度不同，因此將帶來轉動慣量的誤差，高壓壓氣機葉片較小，此影響不大，而風扇/渦輪葉片，其影響很大。在整機三維動力學模型中，建議采用等效環處理方法，以準確考慮各級葉片轉動慣量的動力學影響，并且可以降低自由度和剔除盤片耦合振動。

等效環處理方法是在輪盤外圈建立一個圓環結構以模擬葉片對轉子橫向振動的影響。所建立等效圓環的極轉動慣量 Jp和總質量 m 如式（6）和（7）所示

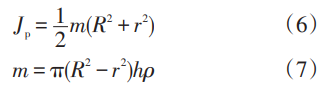
式中 r 是等效圓環的內徑，由輪盤實際外緣半徑 確定；R 是等效圓環外徑，由葉片長度確定；h 是等效 圓環的厚度，ρ是等效圓環密度。所建立圓環的 Jp和 m 應與實際結構整圈葉片的數值相同，因此聯立式（6）和（7）可求得等效環的關鍵參數：厚度 h 和密度 ρ 。據此可在各級輪盤外緣建立等效環。

（2）套齒連接結構

套齒連接結構是低壓轉子系統常用的連接方式，橫向載荷、定位面配合緊度、預緊力、定位間距和接觸面積等諸多參數都對套齒結構的連接剛度存在 影響，進而影響整個轉子的動力學特性。采用 接觸模型雖然可以準確考慮套齒結構的剛度影響， 但無法應用于整機模型。整機有限元模型中，可使用當量剛度方法，即首先采用接觸模型獲得套齒連接剛度的關鍵影響參數和影響規律，再根據實際工作狀態，確定當量剛度值，在模型中通過修改套齒材料彈性模量參數的方法，以獲得相應的當量剛度值。

（3）支承剛度

在ANSYS 中可采用 COMBIN14 模擬一般的線性支承單元，采用 COMBIN40 模擬帶有間隙的支承，采用 COMBIN214 模擬隨轉速變化支承剛度的支承，即 COMBIN214 可以對轉子支承的動剛度進行模擬。值得注意的是，在整機動力學模型中，無論采用哪種單元，其剛度應為鼠籠或彈性環等彈性支承的剛度；而在傳統的轉子動力學模型中，COMBIN 單元應為“彈性支承+承力機匣”的串聯剛度，以降低轉子振動特 性的求解誤差。

2.4 靜子典型結構建模方法

類似渦輪導向葉片的搭接、銷接等柔性連接結構，在 ANSYS 中可使用 MPC184 多點約束單元來對其力學影響進行等效；靜子葉片可采用集中質量法或前文提到的等效圓環法，關鍵是準確考慮葉片質量對靜子動力特性的影響；幅板結構，可參考文獻提出的簡化原則，保證簡化前后的橫截面積不變，彎曲剛度不變，剪切模量不變，沿縱向的質量分布不變；類似火焰筒的帶小孔結構，可直接忽略小孔對振動特性的影響；附件系統可采用子結構法來考慮其剛度和質量對機匣的動力特性影響。

3 算 例

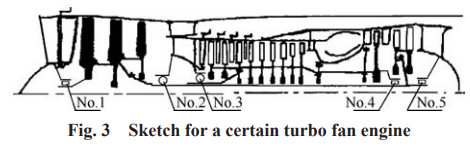
某雙轉子渦扇發動機的總體結構簡圖如圖3所示，高、低壓轉子同向旋轉，高壓轉子支承于 3 號和 4 號支點，其中 4 號為中介支點，低壓轉子支承于 1 號、 2 號和 5 號支點。對其采用八節點六面體實體單元建立整機動力學有限元模型，總自由度數為 621，280， 其中轉子系統自由度數為 211，630。

3.1 正反進動頻率曲線

采用 ANSYS固有模態求解模塊，代入高低壓轉速關系，考慮陀螺力矩的影響，獲得轉子振動為主的各階模態正、反進動隨低壓轉速變化曲線如圖 4 所示。可見，由于高低壓轉子之間以及與靜子系統的振動耦合影響，轉子振動的動頻曲線非常密集，各階振動隨轉速變化規律也各不相同。

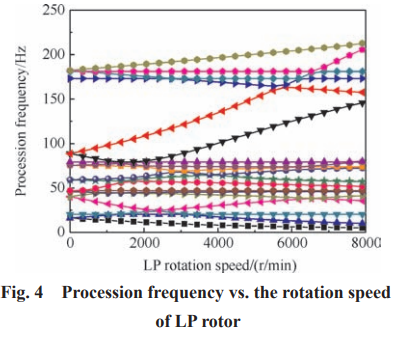
3.2 臨界轉速分析

在圖 5 基礎上進一步繪制轉子不平衡激勵隨轉速的變化曲線 ，即可以求 得雙轉子系統的臨界轉速。值得注意的是：①由于此發動機為順轉轉子，因 此高、低壓不平衡激勵只能激起系統的正進動臨界轉速，在圖 4 中所有反進動曲線可以被剔除。②航空發動機的轉子動力學設計中，主要關心的是不平衡激勵引起的轉子橫向振動，因此在臨界轉速求解時， 軸向振動和扭轉振動可以被剔除。軸向振動由于不受陀螺力矩的影響，因此在圖 5 中，其動頻曲線特征是不分叉的，并且隨轉速增加基本不變。③由于兩個轉子通過中介軸承相連，高壓的不平衡激勵將通過中介支點傳至低壓轉子，反之亦然。因此在 Camp? bell 圖繪制中，需要同時考慮高、低壓轉子的不平衡 激勵。

綜合考慮上述因素，代入高低壓轉速關系曲線， 繪制 Campbell 圖如圖 5 所示。圖中，n=1，…，7 為轉 子系統的各階正進動頻率曲線；低壓激勵為一條射線，其與各階正進動曲線的交點即為低壓轉子激起的臨界轉速，如圖中圓點所示。由于發動機主要工作于慢車至最大轉速區間，因此臨界轉速點 A 應給與重視，求得在慢車轉速工作時，其共振裕度為21.1%， 在巡航轉速工作時，其共振裕度為 22.3%，滿足大于 20%的臨界轉速裕度設計要求。

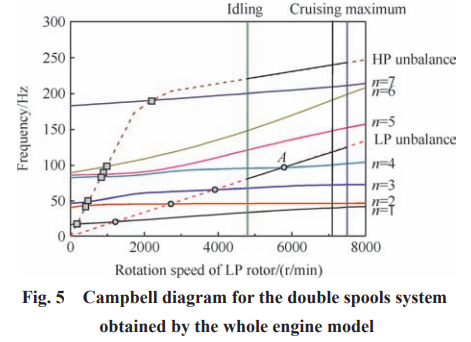
圖 5 中高壓激勵為一條復雜變化的曲線，由高低壓轉速匹配關系所決定。其與各階正進動曲線的交點為高壓轉子激起的臨界轉速，如圖 5 中方塊所示。對此發動機而言，在啟動過程中將快速通過多階高壓激起臨界轉速，但在慢車至最大轉速區間，并不存在臨界轉速，并且在各穩定轉速工況，滿足大于 20% 的裕度要求。

3.3 振型與應變能分析

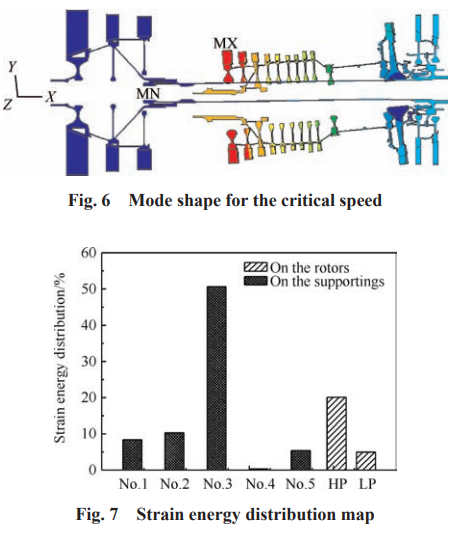
對于臨界轉速點 A，給出其臨界轉速振型如圖 6 所示，可見，此階臨界轉速對應振型以高壓轉子為主（平動），而低壓轉子風扇段基本沒有變形，只是渦輪段略有平動，整體而言屬于轉子的剛體振型。

在該振型下，整機應變能分布如圖 7 所示。高壓壓氣機前支點的應變能最大，即圖 3 中的 3 號支點，達到了整個系統應變能的 50％以上，而高壓轉子本身的應變能較小，占系統的15％左右，在 3 號支點處合理設計支承剛度和阻尼結構是振動抑制的有效措施。總體而言，發動機的應變能主要集中于靜子系統，而轉子系統的總應變能不超過 20%，因此發動機雖然變轉速工作，反復通過臨界轉速點 A，但不會引 起轉子軸系的有害應變積累，滿足航空發動機對臨界轉速點的應變能設計要求。

3.4 與傳統模型計算結果對比

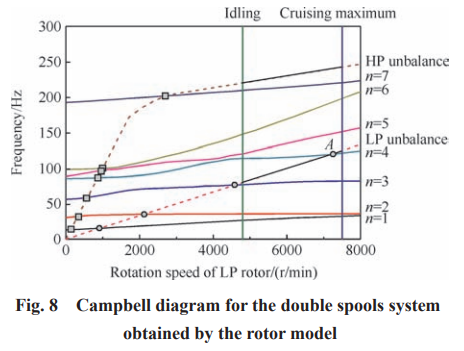
前文給出了采用整機模型獲得的低壓轉子激起 臨界轉速值（5770r/min）。如果將靜子系統考慮為支 點靜剛度，采用傳統的轉子動力學模型求解，最終獲得 Campbell 圖如圖 8 所示，對應低壓轉子激起臨界轉 速為 7243r/min，兩者相對誤差為 25.5%。工程實踐表明，整機模型的計算結果具有更高的精度。

4 結 論

航空發動機由于轉、靜子剛度接近，傳統轉子動力學模型將導致最大 67%的固有模態頻率的計算誤差，因此需要采用整機動力學模型對發動機的臨界轉速進行計算分析。

雙轉子渦扇發動機的高、低壓轉子不平衡激勵 可能激起轉子系統的多階臨界轉速，但在慢車至最大轉速區間內只存在一階高壓平動振型，并且在各 轉速工況均滿足大于 20%的共振裕度要求。對應的應變能分布主要集中于靜子系統，而轉子系統的總應變能不超過 20%，因此在發動機反復通過臨界轉 速點 A 的工作過程中，不會引起轉子軸系的有害應變積累。