1蒙特卡羅賭場
蒙特卡羅(Monte Carlo)是摩納哥公國(Principality of Monaco)的一座城市。摩納哥公國坐落在法國的東南方,總面積為2.02平方公里,是世界上第二小的國家,也是一個從地圖上看容易被忽略的國家。
摩納哥的位置非常小,不仔細看都發現不了

傍晚時分,靜謐的蒙特卡羅賭場
重新豪裝后的蒙特卡羅賭場吸引來了無數賭客,成為當時有名的不夜城。
在蒙特卡羅賭場中,輪盤(Roulette)一直是最受歡迎的項目,因為賭客一直覺得這種賭法有較大的獲勝機會。原來輪盤上有37個格子,其中有18紅格,18個黑格,1個綠格。賭客隨意押注紅格或者黑格。理論上說,出現紅色的概率和黑格的概率是一樣的,一旦出現黑色的次數超過了5次,那都是一個非常小概率的事件,而在這種情況下很多賭徒會賭紅色,即執行這類反方向的策略。
輪盤賭具
1913年的8月13日,賭客還是像往常一樣賭輪盤,其中有不少人拿著紙和筆不停記錄每次輪盤轉下來的結果。但就在當天,輪盤上的小球連續26次落在了黑格上。而這樣事件發生的概率僅為0.00000149%(比中雙色球一等獎的概率還小),這種情況可以說幾乎不可能出現,但確確實實是出現了。賭徒因此損失了大量的財富,因為他們錯誤地認為,先前結果的不平衡性一定導致后面出現相反的結果。
這或許就是人類思維和數據思維差異。實際上,每一次輪盤的轉動都是獨立事件,前面一次小球停留的位置,和下一次小球停留的位置不會有任何關聯。無論小球停在紅色或者黑色的位置,都是隨機的,并不會受到之前結果的影響。
當然,從更宏觀的角度來說,無論賭局規則怎么變化,賭場必定要賺錢的。賭場精心設計各種規則的賭局,讓人們樂在其中的同時,賭場收取少許手續費。正是這種少許的手續費,讓賭場經營者得以生存和擴大,而賭客之間則進行負和博弈,從長期來看,賭客是虧損的。
2蒙特卡羅方法誕生
時間來到1946年,也是蒙特卡羅大賭場誕生的90周年。

烏拉姆急沖沖地把這個方法告訴給他的同事,著名數學家馮·諾依曼(John von Neumann),馮諾依曼確定這個方法是一個重大突破,并且很快在ENIAC(ENIAC是世界上最早期的計算機)電腦上完成了編程。
ENIAC,世界上最早期的電腦,可以占據一個超大房間
為了保密起見,需要給這個程序起一個名字。烏拉姆和馮諾依曼的同事,著名物理學家尼古拉斯·梅特羅波利斯(Nicholas Metropolis)提議名字取為Monte Carlo,以紀念蒙特卡羅大賭場,原因是烏拉姆的叔叔不了解概率,經常在那里輸錢。
但這個蒙特卡羅方法(Monte Carlo Method)需要大量的隨機數,而真實的隨機數并沒有那么多,怎么辦呢?當然在數學家們面前這不可能成為一個障礙,馮諾依曼順手解決了這個問題,進一步發展了隨機數生成器技術(Pseudorandom number generator, PRNG)。
隨后,蒙特卡羅方法被大量地用于曼哈頓計劃(Manhattan Project)中的各項計算和模擬,解決了大量以往確定性方法不能解決的計算問題。20世紀50年代,在LANL實驗室中被用于氫彈的研發,再往后開始在各個領域被大規模地運用,帶來了一場新的思想革命。人們發現,除了傳統確定性方法以外,原來還有一種有效的計算方法,叫蒙特卡羅方法。
曼哈頓計劃集中了大量優秀的科學家,利用核裂變反應來研制原子彈,最后取得圓滿成功
3蒙特卡羅算法是怎么回事
事實上,蒙特卡羅方法非常簡潔。我們用一個例子來說明,如何用蒙特卡羅方法近似得到圓周率?
我們先設置一個1×1的空間,在這個空間中以點(0,0)為圓心,畫一個半徑為1的圓,在1×1空間中留下四分之一圓。
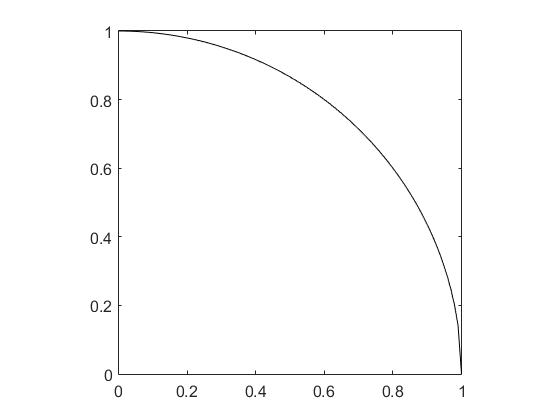
從理論上分析,在1×1的空間的空間中,有這樣的關系:

只要得到四分之一圓的面積與正方形的面積之比,所以可以知道圓周率是多少。
從蒙特卡羅方法的角度看,在1×1這個區間上可均勻地投放大量的點。這些點投到四分之一圓內的概率,近似等于投到四分之一圓內點的比例,即:

所以,我們可以通過計算點個數的方式,來近似得到圓周率的數值。
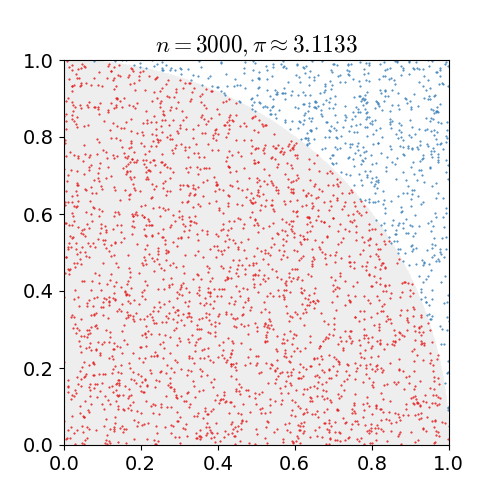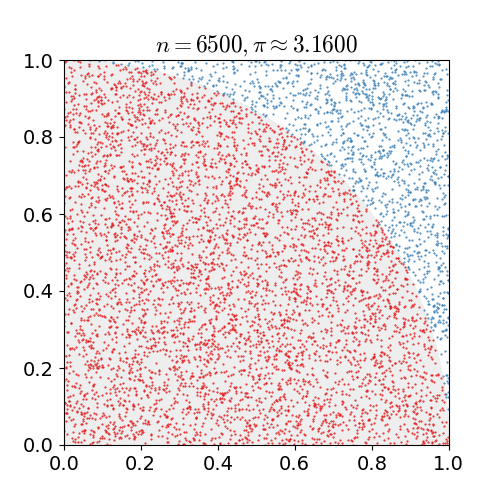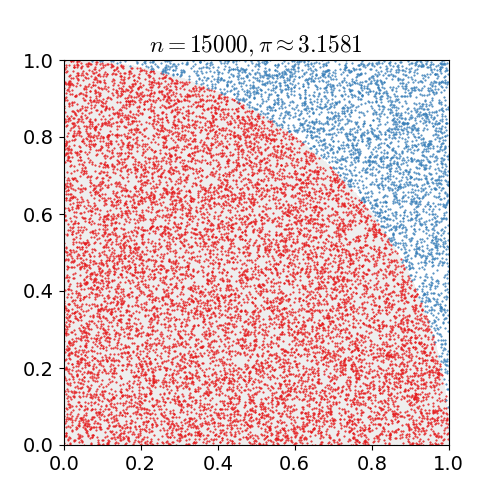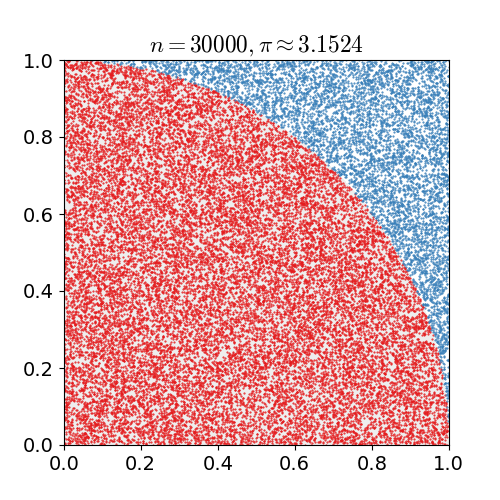
把大量的點投在1×1的空間中,計算落在圓弧內的數量,以估算圓周率π
這種數點的方式雖然簡單,但看起來不是那么靠譜,能否證明蒙特卡羅方法的有效性呢?
實際上已經證明,隨著模擬次數N的增加,蒙特卡羅所得到的近似值與目標值的誤差將以N-0.5的速度降低,結果將越來越精確(可用方差的定義展開進行證明)。

誤差隨著模擬次數的增加而不斷下降,速率為N-0.5
4蒙特卡羅算法的案例
隨著蒙特卡羅方法的成熟及更廣泛的使用,便出現了很多基于蒙特卡羅方法的新算法,用一個時髦的名詞就是:蒙特卡羅“硬分叉”了。
蒙特卡羅積分(Monte Carlo intergration)
在低維的情況下,用確定性的方法來計算積分效果非常好。但到高維的時候,一方面計算難度呈指數級增加,產生維數災難(curse of dimensionality),另一方面在多維的情況下,邊界的確定非常困難,100維以上基本不可能用確定性方法來計算。
蒙特卡羅方法跳出了維數災難的想法,提供了一個新的思路:在高維空間中產生大量的點,采用類似近似計算圓周率的方法,計算高維積分。使用蒙特卡羅方法,誤差將以N-0.5的速度降低,不管維數是多少,只要提升4倍數量的點,誤差將降低一半。因此蒙特卡羅方法非常適合運用在高維的積分計算當中。
如何計算小沙堆體積?用蒙特卡羅積分法即可

一個可愛的機器人,它會識別眼前的環境
在這個一維空間上,機器人通過前期的探索,已經知道這個空間一共有3個外觀都是一樣的門,并記錄了門口的樣子。
問題來了,機器人怎么確定自己在哪里呢?
Step 1:機器人在這個一維空間上隨機生成大量的粒子,每一個粒子分別代表一種位置的可能性(稍后將闡述實際含義)。

Step 2:機器人通過攝像頭發現自己站在一個門口前面。由于機器人已經知道室內地圖,知道門口具體在哪幾個位置,因此機器人重新分配所有粒子的權重,將室內地圖門口所在位置范圍的粒子權重相應提升上來。

Step 3:機器人根據權重分布,重新生成新的粒子。權重越大的地方獲得的粒子越多。

假設機器人繼續往前移動一小段距離:
Step 4:機器人到了一個沒有門口的地方,同時所有的粒子跟隨著機器人移動。

Step 5:機器人發現眼前沒有東西。由于機器人已經知道室內地圖,知道門口具體在哪幾個位置,因此機器人重新分配所有粒子的權重,將室內地圖門口所在位置范圍的粒子權重相應降低下來。


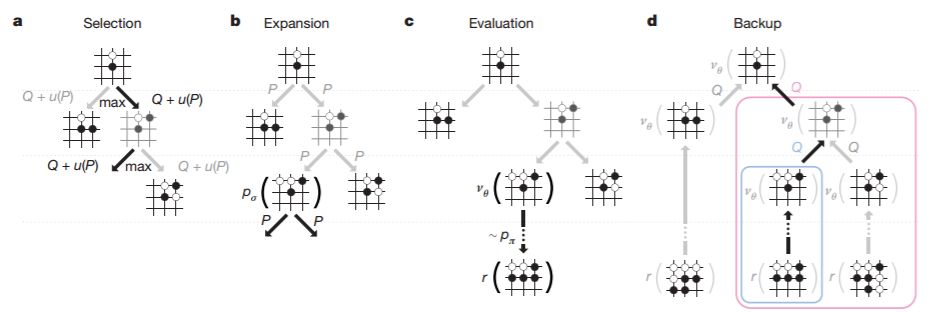
AlphaGo當中的MCTS
元啟發式算法(Metaheuristic)
自從蒙特卡羅方法誕生后,元啟發式算法的發展才正式開始。比如模擬退火算法(Simulated Annealing)、遺傳算法(Genetic Algorithm)、螞蟻算法(Ant Colony Optimization)等等,這些帶有隨機性的算法都是解決組合優化問題的好方法。
2006年NASA在ST5航天器上搭載了一個特別的天線,其形狀由進化算法設計而成
在過去漫長的歲月當中,人們都認為必須要經過嚴謹的推理和計算,才能得到最后正確的答案。直到最近的數十年,隨著計算機的誕生,還有烏拉姆、馮諾依曼以及眾多理解蒙特卡羅方法的科學家的努力下,隨機性的運用才逐漸走進我們的視野。人們意想不到地發現隨機性是一個如此重要的思維,隨機性并非如想象中那樣是一個不好的事物,合理地利用隨機性,能夠幫助我們探索前所未有的世界。
蒙特卡羅方法的發明,是人類思維史上的一個重大突破。一個隨機性的構想,打破了過去的思考空白區,開啟了人類新的思維空間。
-
機器人
+關注
關注
213文章
29756瀏覽量
213041 -
蒙特卡羅
+關注
關注
0文章
11瀏覽量
21331
原文標題:一個徹底改變世界的思想
文章出處:【微信號:WW_CGQJS,微信公眾號:傳感器技術】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
機器人測試:從虛擬到現實,機器人如何才能變成真正的打工牛馬?

盤點#機器人開發平臺
【「# ROS 2智能機器人開發實踐」閱讀體驗】機器人入門的引路書
馬拉松賽場“掉鏈子”?解鎖人形機器人通信穩定秘籍!






 從賭具演變成一個改變機器人發展歷史的思想深挖
從賭具演變成一個改變機器人發展歷史的思想深挖












評論