本文提出雙向塊浮點（BBFP）量化格式及基于其的LLMs加速器BBAL，通過雙向移位與重疊位設計顯著降低量化誤差，提升非線性計算效率，實現精度、吞吐量和能效的顯著優化，相關成果被國際頂級會議 DAC 2025 接收。

序言

在自然語言處理、文本生成和機器翻譯等諸多任務領域，大型語言模型（Large Language Models, LLMs）已然取得了令人矚目的顯著進展，其強大的建模能力與泛化能力展露無遺。然而，隨著模型參數規模的持續攀升，LLMs在計算與存儲資源消耗方面呈現出急劇上升的態勢，這嚴重制約了LLMs在移動設備、嵌入式系統等資源受限環境中的應用拓展。因此，如何在確保模型推理質量不受損的前提下，有效降低計算和存儲開銷，已然成為當前LLMs研究領域亟待攻克的難題之一。

量化技術（Quantization）因其在減少模型大小和計算復雜度方面的有效性，被廣泛用于LLM的高效推理優化。傳統的浮點量化方法（如FP16或FP8）雖然能夠保持較高的精度，但由于其計算復雜度較高，難以在硬件層面高效執行。相比之下，整型量化（如INT8或更低的INT4）能夠大幅降低計算資源需求，提高推理速度。然而，LLMs中的權重和激活值通常具有較大的數值范圍，并且存在顯著的離群值（outliers），這使得簡單的整型量化容易造成信息丟失，從而導致嚴重的精度下降。為了解決這一問題，研究人員提出了更具適應性的量化方法，如Block Floating Point（BFP），該方法允許一組數值共享相同的指數部分，從而在保持相對較高精度的同時降低計算復雜度。

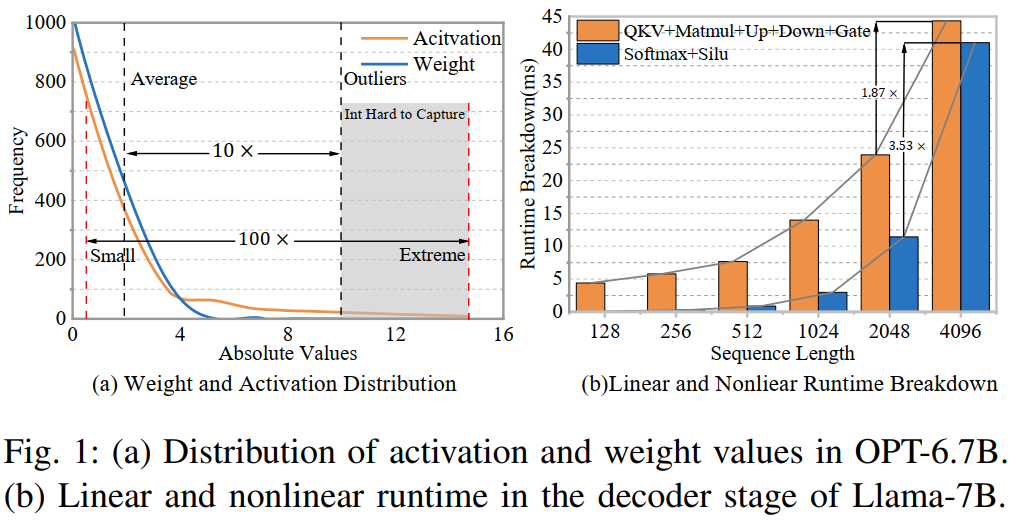
盡管BFP在理論上具備良好的計算效率，但其在實際應用中仍然面臨諸多挑戰。首先，BFP通常通過將所有數值對齊到該塊內的最大指數，以確保數值范圍的統一性。然而，這種策略會導致較小數值的信息丟失，進而引入額外的量化誤差。其次，現代Transformer架構中包含大量非線性運算，如Softmax和SiLU等函數，這些運算通常依賴高精度的浮點計算。由于BFP的舍入誤差較大，直接應用于非線性層可能會導致模型性能的顯著下降。此外，現有的BFP加速器大多專注于線性層的優化，而忽略了非線性層的計算需求，這使得其在整體推理效率上的提升受到限制。

在此背景下，本文提出了一種名為雙向塊浮點（Bidirectional Block Floating Point, BBFP）的新型數據格式，旨在解決BFP在小值和中等值表示上的不足。BBFP通過引入標志位（Flag Bit）和重疊位（Overlap Bits），實現了雙向移位機制，從而增強了對異常值的保護能力并顯著降低了量化誤差。此外，基于BBFP的特性，本文設計了一個高效的非線性計算單元，并最終構建了一個專為LLMs優化的加速器，命名為BBAL（Bidirectional Block Floating Point-based Accelerator for LLMs）。BBAL通過集成優化的處理單元（PE）陣列和非線性計算單元，實現了高效的LLMs推理，為邊緣設備上的模型部署提供了新的思路和技術支持。

本文的主要貢獻可以總結為以下三點：

BBFP數據格式：提出了一種新型量化格式BBFP，通過雙向移位和重疊位設計，增強了對小值、中等值及異常值的表示能力，相較于傳統BFP顯著降低了量化誤差。

非線性計算單元：基于BBFP的共享指數特性，設計了一個高效的非線性計算單元，采用分段查找表（Segmented Lookup Table）方法，降低了資源消耗和延遲，同時保持高精度。

LLMs加速器：構建了BBAL加速器，集成了基于BBFP優化的PE陣列和非線性計算單元，在精度、吞吐量和能效等方面實現了顯著提升。

相關工作

2.1 量化技術

隨著深度學習模型的參數規模不斷擴大，計算和存儲效率成為影響模型部署的關鍵因素。在眾多優化策略中，量化技術因其在降低模型計算復雜度和存儲需求方面的有效性，被廣泛應用于大規模神經網絡的優化。量化的基本思想是將高精度的浮點數（如FP32或FP16）轉換為低比特的數值表示形式（如INT8、INT4甚至更低的BIT-NET），從而減少計算過程中的位寬需求，提高計算吞吐量，并降低內存帶寬占用。對于大型語言模型（LLMs）而言，量化技術尤為重要，因為LLMs通常包含數十億甚至上百億個參數，直接使用高精度浮點運算會帶來巨大的計算開銷。

近年來，針對LLMs的量化技術取得了重要進展。例如，SmoothQuant通過平滑異常值分布來提高量化精度，而GPTQ則利用混合精度方法在低位寬下實現高效量化。盡管這些方法在一定程度上緩解了精度損失問題，但在極低位寬（如4位或更低）下，仍然難以完全滿足LLMs的高精度需求。此外，量化方法通常分為訓練后量化（Post-Training Quantization, PTQ）和量化感知訓練（Quantization-Aware Training, QAT）。QAT通過在訓練過程中引入量化約束，能夠在低位寬下保持較高精度，但其訓練成本對于參數量巨大的LLMs而言往往過高。因此，PTQ因其簡潔性和高效性成為更實用的選擇。本文采用PTQ方法，并提出BBFP以實現無需校準的權重-激活量化。

2.2 塊浮點（BFP）

塊浮點（BFP）是一種介于浮點數和定點數之間的量化格式，旨在結合兩者的優勢。在IEEE-754標準中，單精度浮點數由1位符號位（Sign Bit）、8位指數（Exponent）和23位尾數（Mantissa）組成，其值表示為（v= (-1)s× 1.m×2e-ebias）。BFP通過讓一組數據共享一個最大指數，將浮點運算簡化為定點運算。例如，對于一個向量，其BFP表示可以寫為：

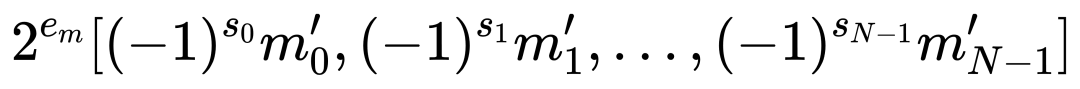
其中，(em)為塊內最大指數，(m'i)為對齊后的尾數。這種設計顯著提高了計算效率和內存密度，因為浮點數的點積運算可以簡化為：

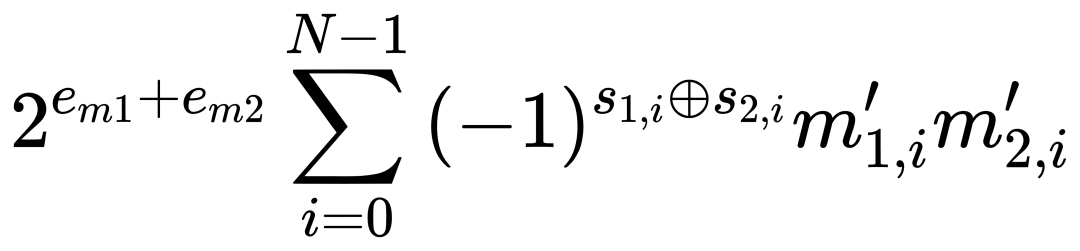
BFP的優勢在于其能夠在保持較高精度的同時降低計算開銷。由于BFP在同一塊內的所有數值共享指數，因此可以將浮點計算轉化為定點計算，從而減少乘法和加法的計算復雜度。此外，BFP的動態范圍比INT更大，使其在處理具有離群值的LLMs時更具優勢。然而，標準BFP仍然存在一定的局限性。例如，在BFP中，所有數值都會被對齊到該塊的最大指數，這意味著較小的數值會被右移，從而可能導致精度丟失。這種現象在LLMs的線性層中尤為明顯，因為它會影響模型的整體推理精度。此外，BFP在非線性層（如Softmax、GELU等）中的應用也面臨挑戰，因為這些層通常涉及超越函數的計算，而BFP的舍入誤差可能放大這些計算的不確定性，導致模型性能下降。因此，如何在保留BFP優勢的同時降低其量化誤差，成為當前研究的重點。

本文方法

3.1 雙向塊浮點（BBFP）數據格式

為了降低傳統塊浮點（BFP）量化過程中由于強制對齊所有數據到最大指數而引起的量化誤差，本文提出了一種改進的量化數據格式——雙向塊浮點（Bidirectional Block Floating Point, BBFP）。BBFP的核心思想是通過引入一個1位標志位（flag bit）來區分高尾數（high mantissa）和低尾數（low mantissa），從而避免所有數值都必須對齊到最大指數。此外，BBFP還采用重疊位（overlap bits）機制，以減少因左移或右移操作帶來的精度損失。

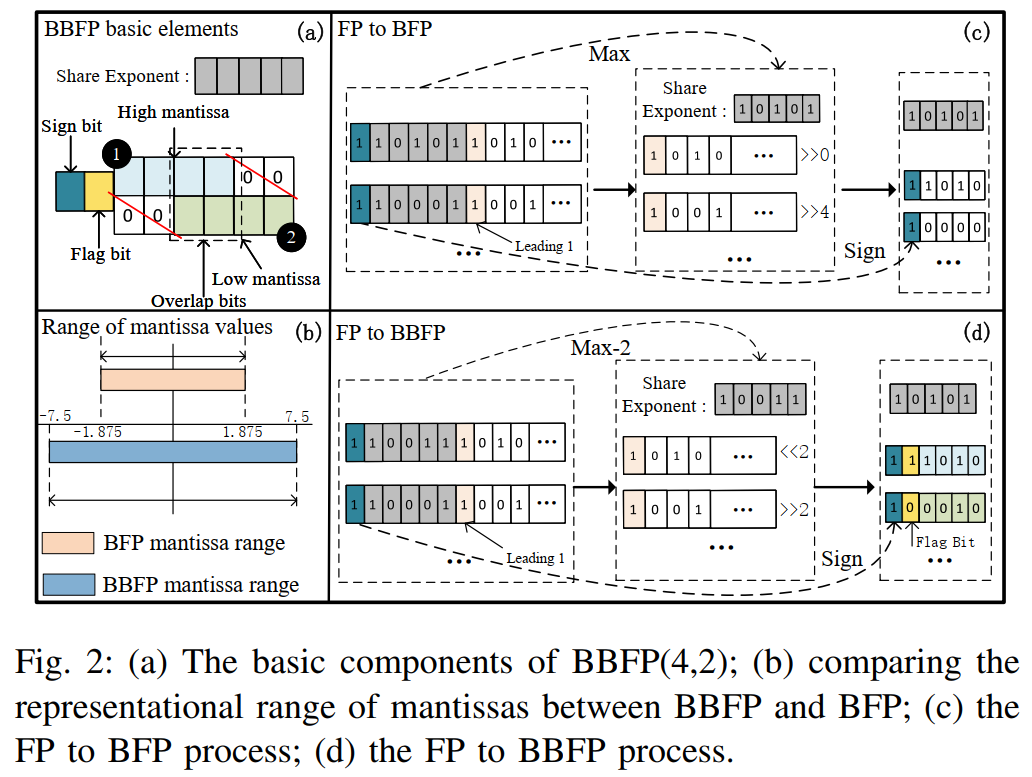
BBFP的結構如圖2(a)所示，它由以下幾個部分組成：

符號位（Sign Bit）：1位，表示數值的正負。

標志位（Flag Bit）：1位，用于指示尾數是否經過左移（高尾數）或右移（低尾數）。

共享指數（Shared Exponent）：固定位數（本文實驗中為5位），用于表示該塊內所有數值的共享指數。

尾數（Mantissa）：m位，表示數值的有效數字部分。

重疊位（Overlap Bits）：o位，用于減少移位操作帶來的精度損失。

BBFP的不同配置可以表示為BBFP(m,o)，其中m表示尾數的位寬，o表示重疊位的位寬。例如，BBFP(4,2)表示尾數為4位，重疊位為2位。與傳統的BFP相比，BBFP的尾數表示范圍更廣（如圖2(b)所示），因為它允許一部分尾數向左偏移，而不是全部向右對齊到最大指數。

在FP16到BBFP(4,2)的轉換過程中，原始FP16值首先被截斷，然后根據共享指數與原始指數的關系決定是否左移或右移。具體而言，轉換公式如下：

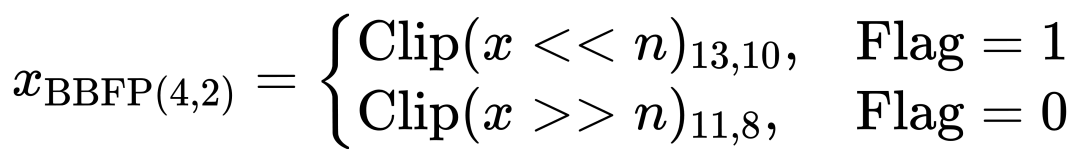
其中，Clip(?)a,b表示從位a到b的截斷操作，n表示移位次數，Flag是1位標志位，用于區分高尾數和低尾數。重疊位的引入使得左移時能夠保留更多高位信息，從而減少截斷誤差。

BBFP的轉換過程如圖2(d)所示：首先確定共享指數（如Max - 2），然后根據原始指數與共享指數的大小關系調整尾數，并通過標志位記錄移位方向，最后將尾數截斷至指定位寬。BBFP的值表示為：

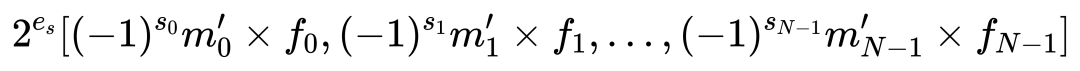
其中，移位因子fi 定義為：

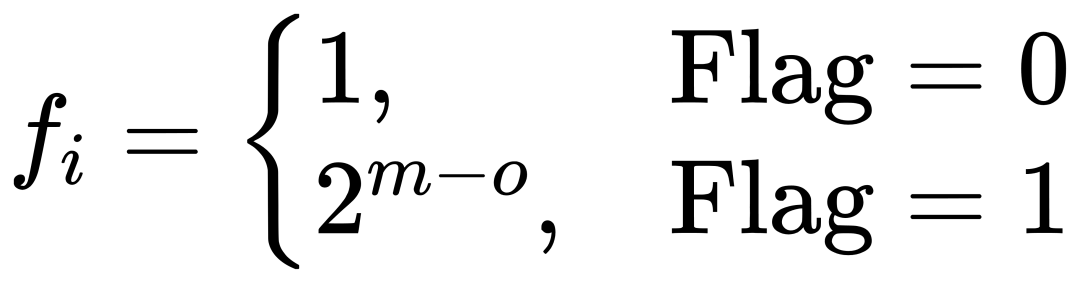
相比BFP，BBFP在相同尾數位寬下顯著提升了表示范圍（如圖2(b)所示），從而更好地保護了小值和異常值。

3.1.1 BBFP的點積計算

BBFP保留了BFP將浮點運算轉換為定點運算的特性，其點積計算公式為：

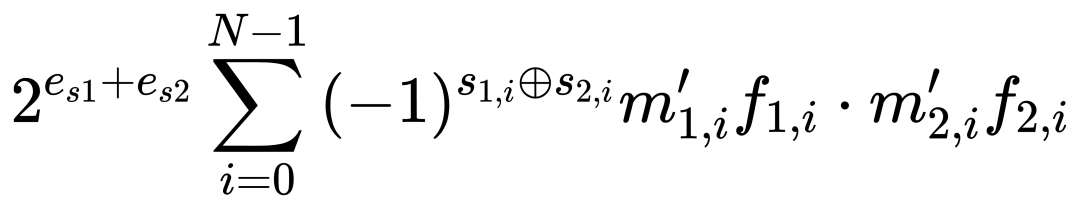
其中，f1,i和f2,i根據標志位確定移位量。通過引入多路選擇器和移位模塊，BBFP將尾數表示范圍擴展了4倍，同時保持了高效的定點計算特性。

3.1.2 量化誤差分析

為了評估BBFP相較于傳統BFP在量化誤差方面的改進，本文對兩種方法的量化誤差進行了理論分析。假設使用最近舍入（round to nearest）策略，BFP的量化誤差服從零均值分布，其方差 σ2可以表示為：

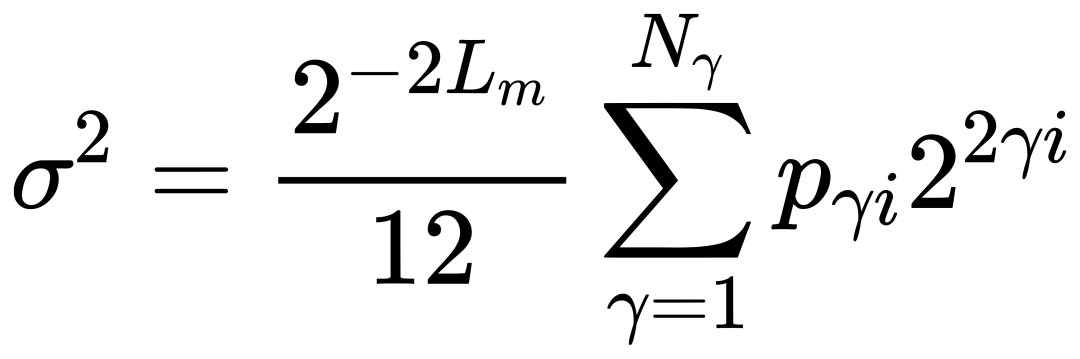
其中Lm表示尾數的長度，pγi表示塊指數的概率質量函數，Nγ=2LE表示可用的塊指數級別數量。當BFP和BBFP使用相同的尾數位寬時，唯一的區別在于pγi的分布情況。由于BBFP減少了對最大指數的依賴，其量化誤差方差也會相應降低。

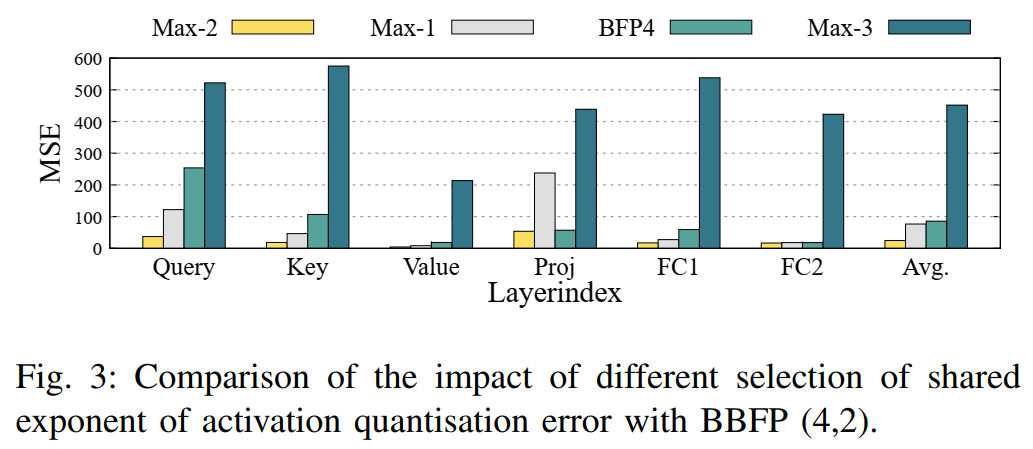
為了驗證這一理論，本文進行了實驗分析。圖3展示了BBFP(4,2)與BFP4在不同共享指數策略下的量化誤差對比。實驗結果顯示，當使用Max?3（即Eshared= Max(E) - 3）作為共享指數時，由于左移操作可能導致最高位溢出，量化誤差顯著增加。相反，當使用Max?1（即Eshared= Max(E) - 1）時，量化誤差較低，但仍高于BBFP自適應選擇共享指數的方式。

3.1.3 共享指數選擇策略

BBFP的共享指數選擇策略對量化誤差有直接影響。本文提出了一種基于尾數位寬和重疊位數量的共享指數選擇方法，即：

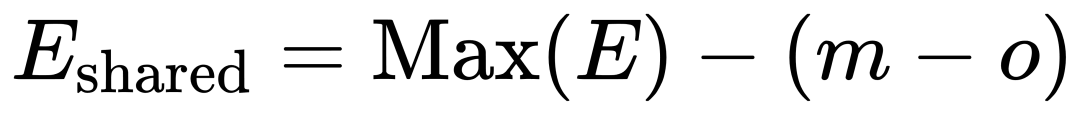
其中，Max(E)表示該塊內的最大指數，m表示尾數位寬，o表示重疊位數量。該公式的核心思想是，通過減少對最大指數的依賴，使部分數值的尾數向左偏移，而不是全部右移對齊。這樣可以有效減少中小數值的精度損失。

3.1.4 重疊位寬度選擇

重疊位的引入有助于減少移位操作帶來的精度損失，但同時也增加了硬件開銷。為了在量化誤差和硬件成本之間取得最佳平衡，本文提出了一種基于模型特性和量化誤差的重疊位選擇方法。具體而言，該方法通過調整算法1中的開銷權重，可以在準確率優先或硬件成本優先之間進行權衡。

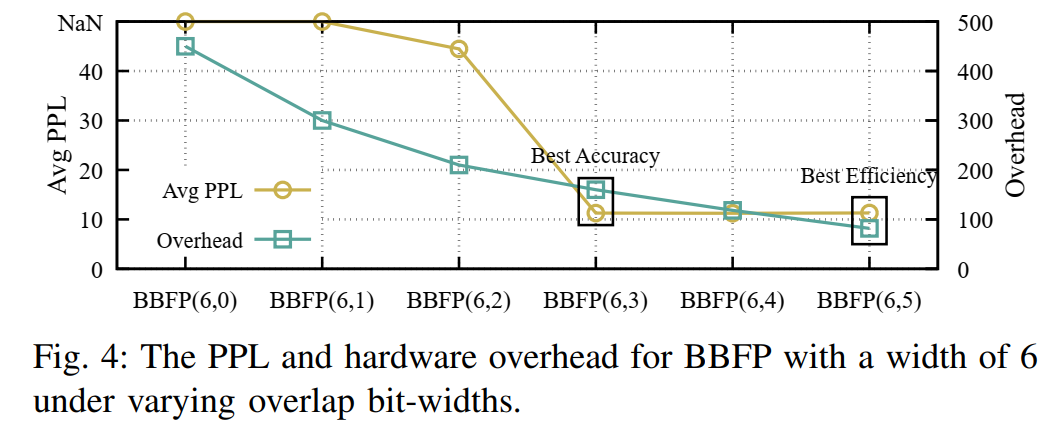
圖4展示了在BBFP(6,0)到BBFP(6,5)不同重疊位配置下的模型困惑度（PPL）和硬件開銷。實驗結果表明，適當增加重疊位的數量可以顯著降低量化誤差，提高模型精度。然而，過高的重疊位數量會增加硬件資源消耗，因此需要根據實際應用場景進行優化。

3.2 數據格式驅動的硬件設計

基于BBFP的特性，本文設計了一種高效的硬件架構，包括優化的乘法累加（Multiply and Accumulate, MAC）模塊和非線性計算單元。

3.2.1 線性計算單元

1. 塊內乘法

BBFP的塊內矩陣乘法分為共享指數加法和尾數乘法。尾數乘法公式為：

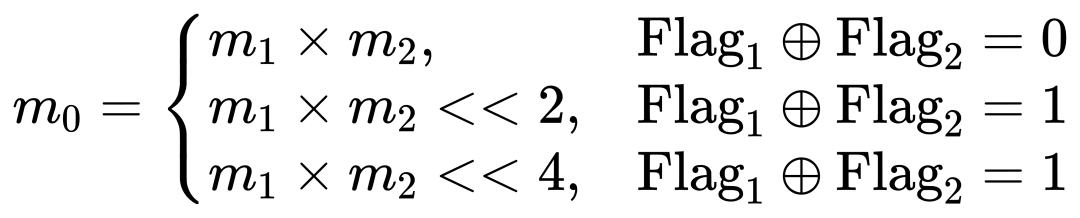
對于BBFP(4,2)，兩個4位尾數的乘法通過4位乘法器實現，隨后進行移位操作得到12位結果（圖5(a)）。為提高內存密度，移位后的零位被移除，并用2位標志表示零元素位置，最終輸出為包含2位標志、1位符號和8位尾數的BBFP格式。

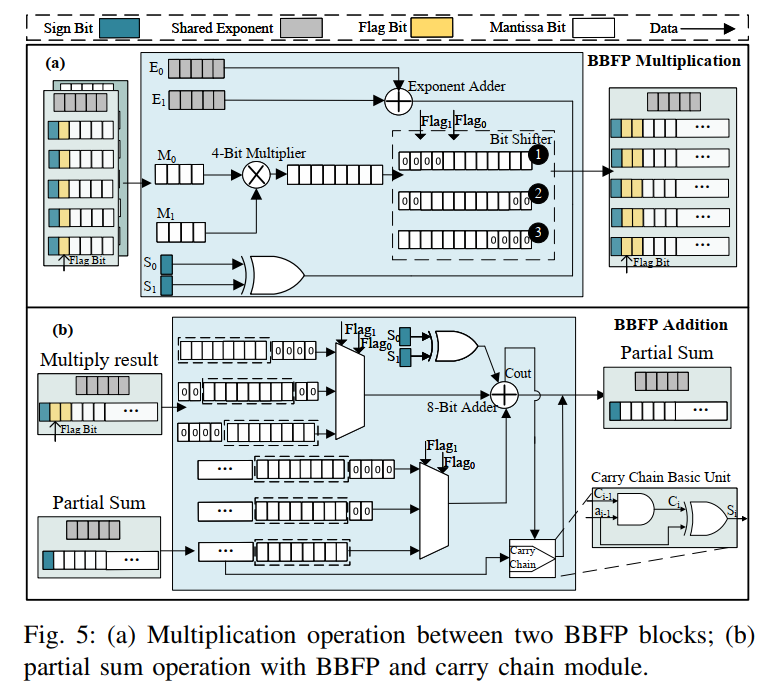
2. 部分和加法

塊內乘法后需進行部分和加法。BBFP的計算結果具有規則的位級稀疏性，本文利用稀疏加法器減少加法器位寬（圖5(b)）。例如，用8位加法器和n位進位鏈替代 ( 12+n ) 位加法器，其全加器表達式為：

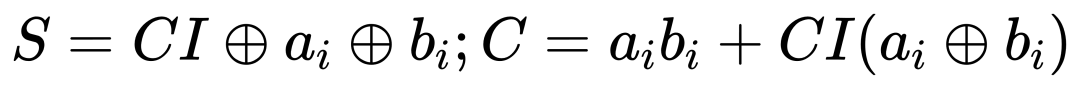
在稀疏模式下，加法器可簡化為：

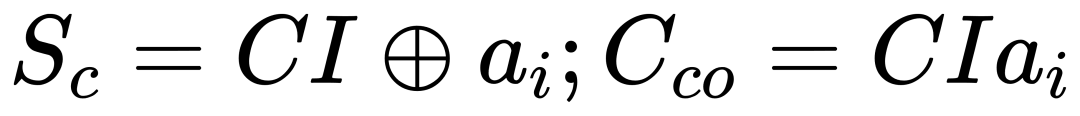
通過這種優化，例如用8位加法器和4位進位鏈替代12位加法器，可減少15%的資源消耗。表I展示了不同數據格式下MAC單元的面積和內存效率，BBFP(6,3) 在面積更小的情況下提供了比BFP8更高的表示能力。

3.2.2 非線性計算單元

1. 分段查找表

BBFP利用共享指數特性，將函數值按指數分段存儲于外部內存。例如，5位指數可生成(25×2 ) 個子表。在對齊階段計算共享指數后，加載對應子表，并直接以尾數作為查找地址，避免了浮點LUT的額外映射開銷。

2. 流水線設計

為提高吞吐量并掩蓋LUT加載延遲，非線性計算單元采用流水線架構，各模塊配備緩沖區。單元支持多種超越函數（如Sigmoid、Softmax），通過可調計算順序和冗余單元實現靈活性。

3. INT計算

數據通過對齊模塊轉換為BBFP后，LUT中的條目也預轉換為BBFP格式，確保計算一致性。圖6展示了以Softmax為例的非線性單元流程。

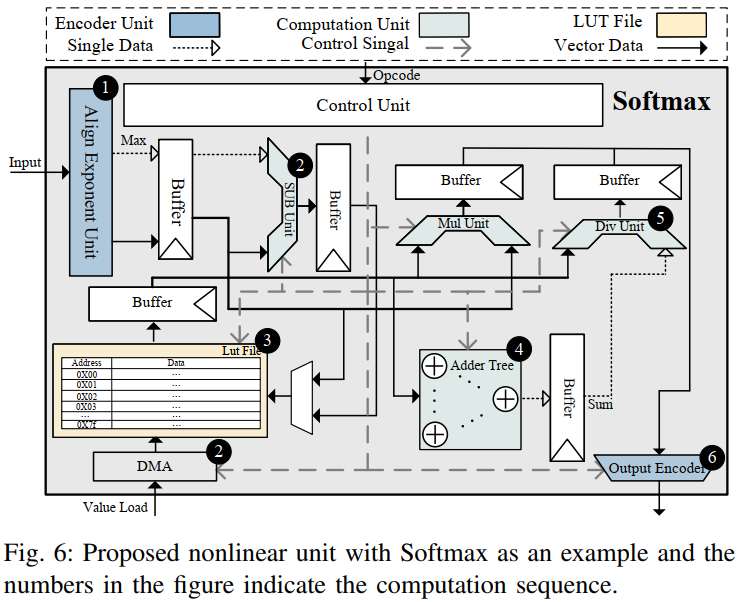
3.2.3 LLMs加速器

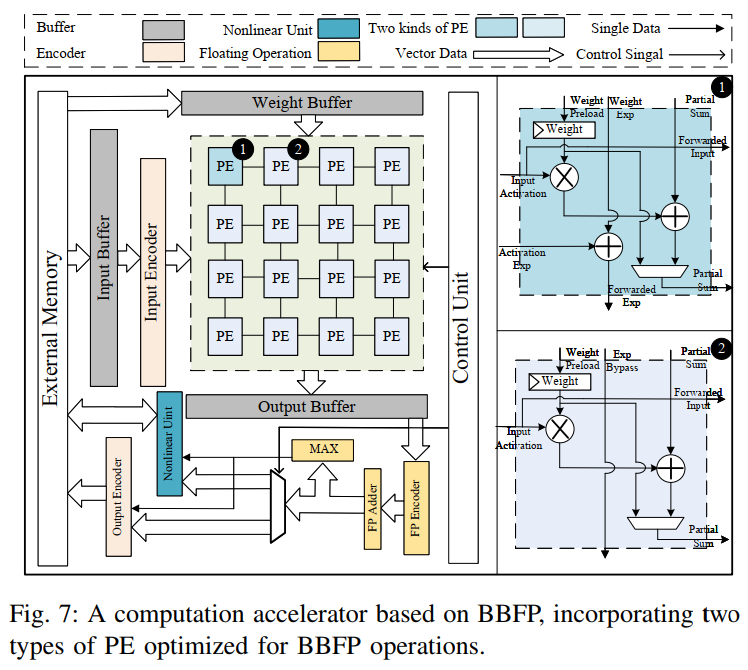
基于上述模塊，本文構建了BBAL加速器（圖7），其核心包括：

PE陣列：基于BBFP優化的處理單元陣列，支持高效線性計算，包含共享指數加法器和旁路單元兩種版本。

非線性計算單元：集成上述設計，實現低成本非線性操作。

其他模塊：輸入編碼器、緩沖區、輸出編碼器等，支持完整推理流程。

3.3 實驗評估

3.3.1 非線性單元的精度與效率分析

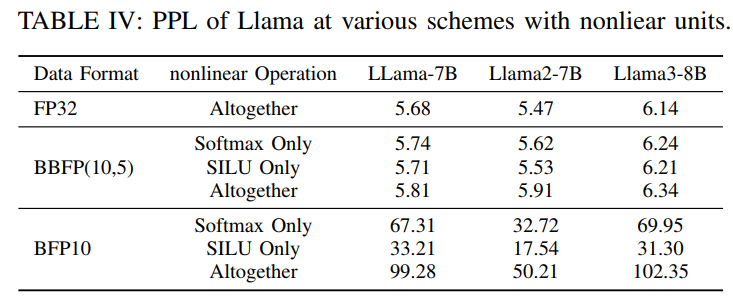
為了驗證BBFP在非線性層中的有效性，本文在Llama-7B、Llama2-7B和Llama3-8B模型上進行了實驗，比較了基于BBFP(10,5)和BFP10的非線性計算單元在困惑度（Perplexity, PPL）方面的表現。實驗結果如表IV所示，可以看出，采用BBFP(10,5)量化策略的模型在使用Softmax和SiLU非線性函數時，PPL的增長幅度遠低于BFP10方案。例如，在Llama-7B模型上，使用BFP10進行Softmax計算會導致PPL增加至67.31，而BBFP(10,5)僅使PPL增加至5.74，接近FP32基線水平。同樣，在Llama2-7B和Llama3-8B模型上，BBFP(10,5)的PPL增長幅度也明顯小于BFP10，表明BBFP在非線性層計算中能夠有效減少量化誤差，保持較高的模型精度。

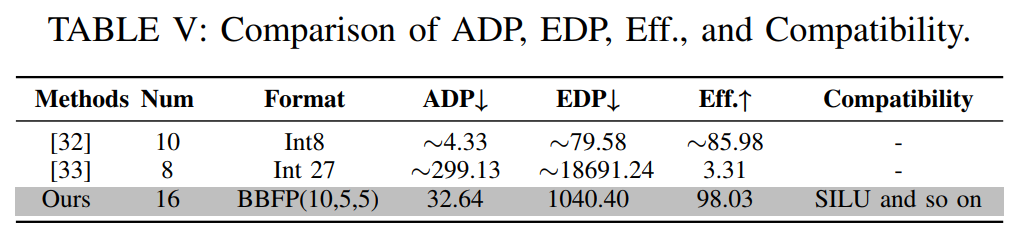
除了精度分析，本文還評估了所提出的非線性計算單元的能效比。表V展示了不同方法在面積延遲乘積（Area Delay Product, ADP）、能量延遲乘積（Energy Delay Product, EDP）以及計算效率（Throughput/(Area×Power)）等方面的對比。實驗結果表明，盡管BBFP(10,5)的ADP和EDP略高于低精度近似算法，但其計算效率顯著優于現有方法。這是因為BBFP(10,5)采用了分段指數動態查找策略，減少了昂貴的片上存儲需求，同時保持了較高的計算兼容性。此外，由于BBFP的尾數表示范圍更廣，其在非線性計算中的精度損失較小，從而減少了對額外校正電路的需求，進一步降低了硬件開銷。

3.3.2 線性單元的面積與精度對比

為了評估BBFP在線性層中的性能，本文在WikiText2數據集上測試了不同量化策略對Llama和OPT系列模型的影響。表II展示了FP16基線模型、BFP4、BFP6以及不同BBFP配置的PPL結果。實驗結果顯示，BBFP在保持較低PPL的同時，能夠有效減少量化誤差。例如，BBFP(4,2)在Llama-7B上的PPL為5.80，而BFP6的PPL為5.61，兩者差距較小，但BBFP(4,2)的計算效率更高。此外，BBFP(6,3)在Llama-7B上的PPL僅為5.48，與FP16基線（5.47）幾乎持平，顯示出其在高精度場景下的優越性。

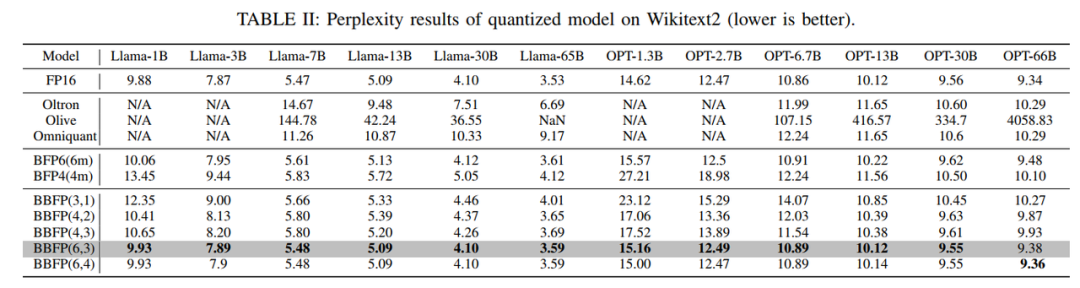
為了進一步分析BBFP的硬件成本，表III列出了不同量化策略下處理單元（Processing Element, PE）的面積消耗。實驗結果表明，BBFP的PE面積略高于BFP4，但相較于BFP6仍然具有優勢。例如，BBFP(3,1)的PE面積僅為77.69 μm2，而BFP4的PE面積為215.23 μm2。這是因為在BBFP中，尾數的高位和低位分別對應不同的移位方向，使得乘法和加法運算的位寬需求有所降低。此外，BBFP的1位標志位雖然增加了少量存儲開銷，但由于其在精度上的提升，使得整體硬件成本得到了優化。

3.3.3 吞吐量與準確率的平衡

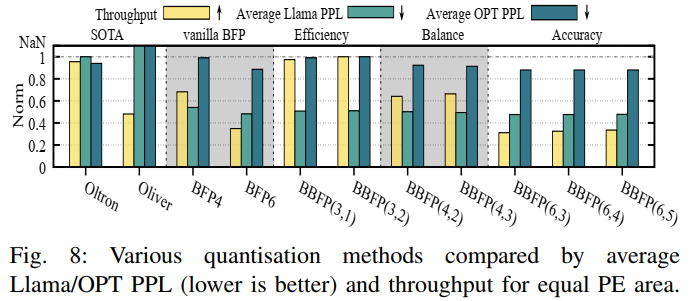
為了評估不同量化策略在吞吐量和準確率之間的平衡，本文在相同PE面積條件下進行了比較分析。圖8展示了不同量化方法在Llama和OPT系列模型上的平均PPL和吞吐量表現?？梢钥闯觯珺BFP(3,1)和BBFP(3,2)在保持較高吞吐量的同時，其PPL遠低于Oltron和Olive等基于離群值感知的量化方法。此外，BBFP(3,1)和BBFP(3,2)的吞吐量與Oltron相當，但準確率更高，這證明了BBFP在吞吐量和準確率之間取得了較好的平衡。

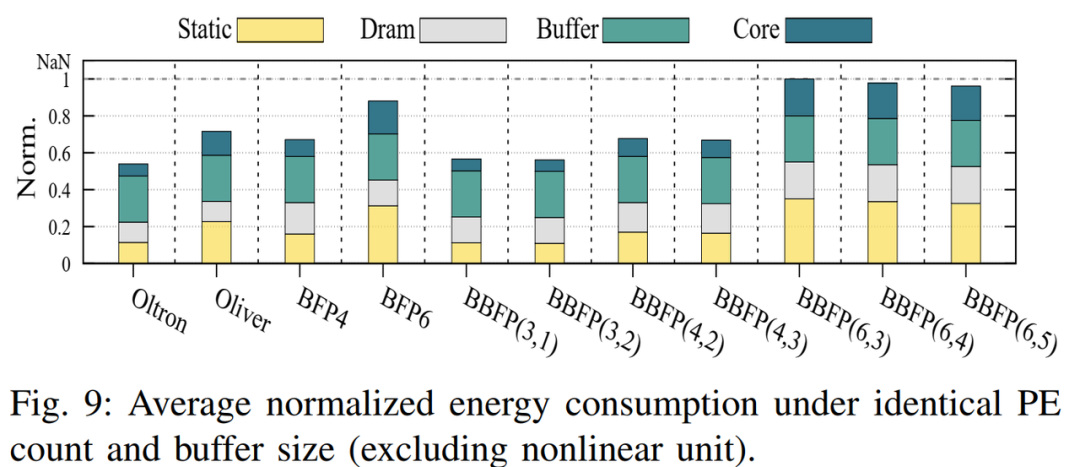
3.3.4 能源效率分析

除了吞吐量和準確率，能源效率也是衡量加速器性能的重要指標。圖9展示了相同PE數量和緩沖區大小下的能耗。BBFP(3,1)相較BFP4降低13%的能耗，主要得益于靜態和核心能量的減少。BBFP與相同位寬BFP的能耗增幅在5%以內，額外標志位對DRAM功耗影響較小。

結論

本文提出了一種改進的塊浮點量化方法——雙向塊浮點（Bidirectional Block Floating Point, BBFP），并基于該方法設計了一款高效的大型語言模型（LLMs）加速器BBAL。BBFP通過引入1位標志位和重疊位機制，有效降低了傳統塊浮點（BFP）量化過程中因強制對齊所有數據到最大指數所帶來的量化誤差。此外，BBFP還優化了共享指數選擇策略，使部分數值的尾數向左偏移，避免了中小數值的精度損失?；贐BFP的特性，本文進一步設計了一種高效的非線性計算單元，該單元結合了基于查找表（Look-Up Table, LUT）的計算方法，能夠在保持較高精度的同時降低計算開銷。最終，本文構建了一個完整的LLM加速器架構BBAL，其中包含了優化的處理單元（Processing Element, PE）陣列和非線性計算單元。實驗結果表明，BBAL在保持與現有加速器相當的計算效率的同時，其模型精度提升了22%；而在保持相近精度的情況下，其計算效率提高了40%。