在一個萬物生發陽光燦爛的日子里,我正規劃著將要設計的電路模塊。這次需要做的是一個高精度高負載調整率帶片外大電容的LDO,來為整顆芯片的低壓部分供電。LDO的IP是剛剛從同事那里Kiang來的,采用了Miller補償的結構,雖然這是一個很靠譜的同事,雖然看上去其中有一些做的比較巧妙的地方,但內心不免是有些疑惑的:面對這么大的輸出電容,Miller補償真的可以嗎?這顆疑問的種子其實早在一個月前就已生根發芽。完整的故事開頭是這樣的,曾經做過一個由DAC控制的Buffer,正負高壓間ClassAB輸出并帶有一個10uF大電容,一般情況下空載,輸出電平調整或者開關機時需要比較大的SR,那么當輸出電流回歸到限流值以內后可以認為開啟了Settling的過程(輸出不再限流表明gm退出了飽和狀態),此時負載電流仍會有一個由較大值變為空載的過程,需要Buffer穩定。考慮到輸出有10uF電容,大部分情況下空載,那么粗算下來輸出極點頻率位置會低到約0.03Hz,并且還有負載電流變化的過程,因而覺得采用Miller補償可能會比較困難,同時考慮到高壓電容的開銷會很大,所以當時決定采用最土鱉的補償辦法(在敲下這段文字的當下,忽然想到其實可以采用分壓和源級跟隨器組合的方式把Miller電容的兩端都放在低電壓域,不禁感覺到一口老血要吐出來了,當年竟如此業余)。
不久前正好有人問起這個電路為什么不采用Miller補償呢?這個電路的應用跟LDO有什么區別呢?雖然巴拉巴拉把上述考慮又搬出來講了一番,但其實我內心疑問的小情緒已然波動起來:是啊,為什么不能采用Miller補償呢?很多時候一提到帶片外大電容的LDO,作為一個沒有正兒八經做過的人,腦海里的第一印象總是先浮現出那些“ESR固定零點”、“零極點追蹤”等等名詞,甚至還沒有經過仔細的推敲就“憑感覺”否定了Miller補償的可能性。事實上,最近找來一些論文看過之后才發現,原來在LDO領域有大量的基于Miller補償的設計方法和案例,還是怪自己書讀的太少了啊!不過機緣巧合的是,上述問題因為前些日子的一個錯誤仿真而得以被仔細捋了一遍,用了盡可能簡單且直觀的方式把Miller效應及補償又翻出來好好理解了一下,現在我把其中仿真錯誤的教訓以及由此而發散的一些思考分享出來,當然有可能理解正確也有可能給出錯誤的解釋,之所以還要厚著臉皮寫出來,權當是希望可以給大家拋磚引玉,作出一點點唯小的貢獻!
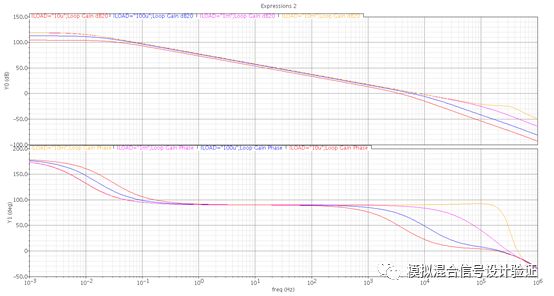
圖1
好了,前戲到此結束,正片開始:拿到同事IP之后,道理我都懂,于是人狠話不多,直接上了手!但是跑完stb仿真之后如圖1所示,當一根略顯完美的單位增益帶寬內單極點的增益曲線躺在你面前時,其實我整個人內心是不安的,原本在極低頻的輸出極點真的能一下子被推到單位增益帶寬以外嗎,即便是在幾乎空載的情況下?恍惚間覺得是不是環路的斷點設置錯了?一直以來都是把環路斷點設置在FB的高阻點,可偏偏這次不自信了,于是把斷點改到了輸出,得到了如圖2的仿真結果。在這樣的斷點條件下仿真發現主極點位置能和輸出極點吻合,但是卻看到多了一個較近的零點和次極點。于是又一次陷入到了深深的疑惑中:次極點難道是因為負載電容太大而使Miller補償失效了的反饋節點處的極點?那么這個零點又是個什么鬼?因為這個Miller補償采用的是接到第一級運放折疊點cascode管源極的Ahuja接法,如圖3所示,第一反應是不是這種接法有什么隱藏的Bug,比如折疊點下方電流源管漏端輸出阻抗下降等。
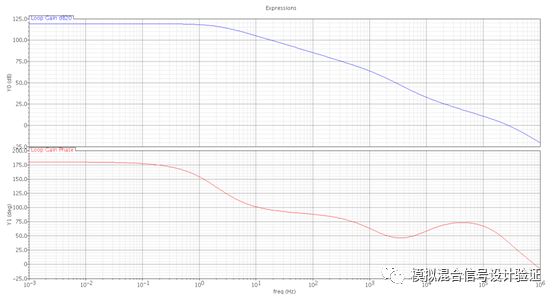
圖2
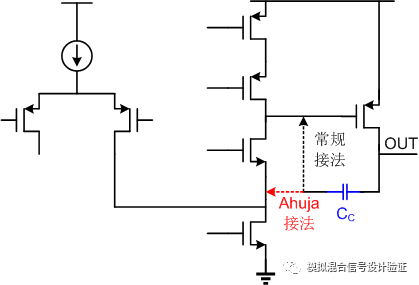
圖3
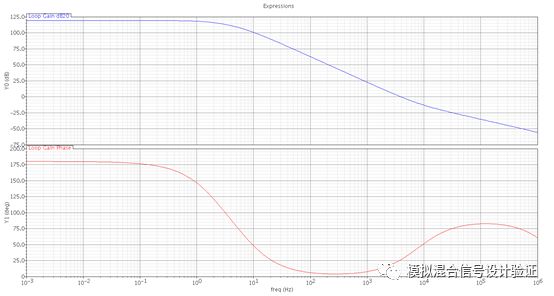
圖4
于是嘗試著將Ahuja接法換成常規接法,仿真stb后發現在低頻有兩個挨得很近的極點,如圖4所示,一個頻率跟輸出極點吻合,另一個看起來像是Miller效應產生的極點,一度以為Ahuja接法由于某種原因讓Miller補償失效了。求助了IC群里的一些朋友,大家給出的答案也并沒能盡釋其中的疑惑。于是我把上述仿真到的現象跟同事一起探討了下,剛開始他在看到波形的時候也是十分懵逼的,或者說被我先入為主的判斷帶溝里了。過了兩天,同事發現了一個突破點,就是他用AC做閉環仿真,帶寬位置是可以跟Miller補償帶寬對得上的。于是,經過與模擬設計人民的老朋友——Paper、書籍還有另一半大腦的一番深入交流之后找到了問題之所在:1.環路斷點確實設錯了; 2. Miller補償在這種負載電容下還沒有失效; 3. 輸出極點被Miller補償推遠了。
這個結論其實非常簡單,也許你會說不就是犯了個低級錯誤所以弄錯了嘛。但是這些天仔細回顧了問題發展的整個過程,我覺得之所以會犯這樣的錯誤,實際上還是學藝不精,并沒有真正吃透Miller效應和Miller補償的原理所致!我們常常都善于去記住一些簡單的結論卻沒有多問一聲“為什么”進而再去dig more。回到結論中的三個點,對于第一個問題,我們可能都有這樣的經驗,環路斷的位置不對經常會出現一些異常的結果,但又不是很明確到底斷在哪里是對的哪里是錯的,為什么是錯的,所以為保險起見常常會挑選一個高阻點,比如電阻分壓反饋FB到運放輸入端的柵極,抑或是同樣為高阻的第一級運放輸出到第二級運放輸入的柵極,如圖5所示。
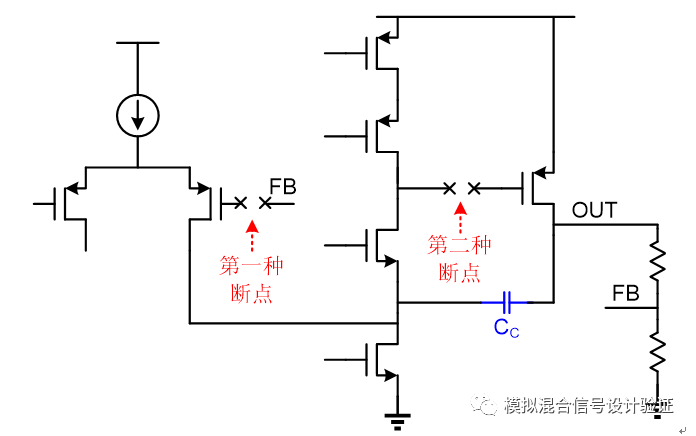
圖5
對本例而言,按第一種方式斷開環路是正確的,而按后者方式斷開環路是錯誤的。那么環路究竟該如何斷開才是合理的呢?從理論上而言,不管系統內部斷開后某個通路歸于前向通路還是反饋通路,雖然計算的環路曲線會不同,但最終計算的閉環曲線應該是能夠殊途同歸的。然而實際中,由于很多電路既有反饋又有前饋,同時還要考慮斷點左右的負載和驅動效應,容易導致仿真器"認錯",所以應該盡量保證內部嵌套的“Local loop”的完整性,斷點也應盡量設置在一條接近純數值比例的路徑,比如電阻反饋到輸入端的通路,使得可以比較清晰簡單的來分析計算環路增益,避免仿真器迭代出一個“看起來不對”的結果。論文“ATransient-Enhanced Low-Quiescent Current Low-Dropout Regulator With BufferImpedance Attenuation”中的Fig.5很好的顯示了這一特點(不過論文中Fig.5有一點小問題,重畫如下圖6所示)。
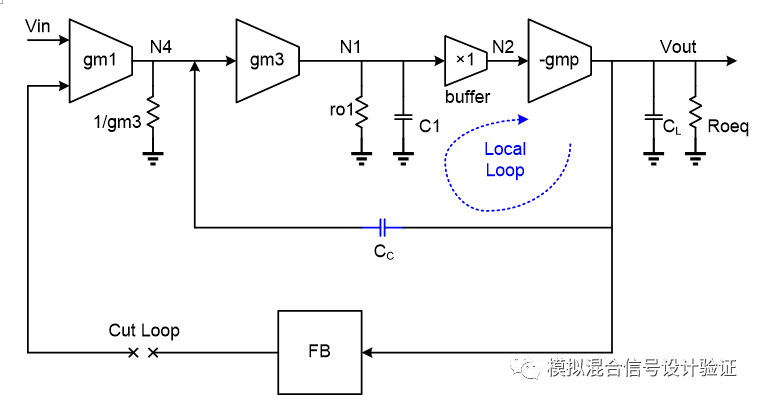
圖6
所以,針對帶有Miller補償的環路,在如何設置斷點這方面,我認為最為重要的原則就是保持Miller反饋小環路的完整性,并且盡可能把斷點設置在常系數的路徑,以免仿真器將來在報道上出現偏差!對于本例而言,上述兩種斷點方案之所以后者也不行是由于這種方式把帶有Miller反饋的小環路給斷開了(跨接電容的第二級運放柵極輸入被斷開了)。
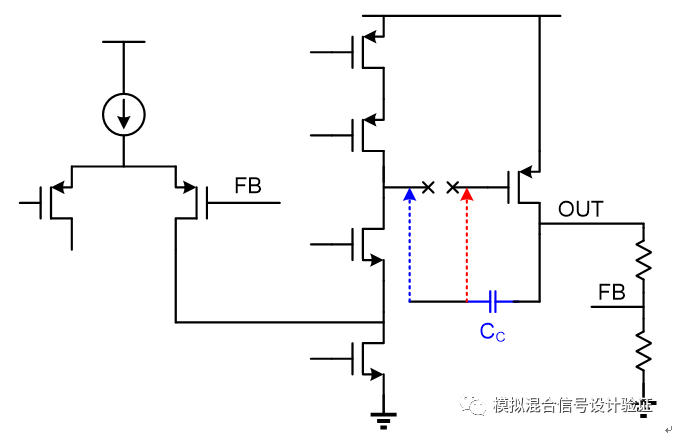
圖7
假設同樣是把環路斷點設置在第一級運放的輸出端,如圖7所示僅僅只是把Miller電容的反饋端分別接到斷點的左右兩側就可以得到完全不同的仿真結果,這就是因為接回到斷點右側時保持了Miller小環路的完整性。上文提到了兩種不同接法的Miller補償仿真得到了兩個巨大差異的結果,也是因為環路斷點被錯誤的設置在了LDO輸出端(嘗試過斷點設置在第一級運放輸出端也是同樣的結果,除非Miller反饋接回點在環路斷點的右側從而保持小環路完整)。由于斷點破壞了Miller補償所在小環路,所以兩種不同接法的Miller補償電路仿真得到的主極點都變成了輸出極點,而次極點在電路中的位置處于電容反饋端,Ahuja的接法電容反饋端接的是低阻點,因此相比于另一種接法所看到的次極點要遠得多。之所以要保證Local Loop的完整性是由于其輸入輸出阻抗由于反饋的作用發生了改變,這個小環路是作為一個整體接入到前向通路中的,如果將其斷開將無法獲得這一特性,因而影響了整條路徑的計算結果,在看完整篇文章的分析后會使你有一個更清晰的認識。
對于前文所提出的第二和第三個結論,實際上可以歸結為同一個問題,也就是Miller極點跟輸出極點的關系,簡單來說是不是當Miller極點與輸出極點相近時就認為Miller補償失效了?我們都知道,采用Miller補償時不僅僅會產生一個Miller極點,同時還會讓主次極點分離。Miller效應會使得在電容所跨接的運放輸入端看到了一個被放大了AM倍的等效電容(AM是跨接在電容兩端運放的開環增益),但是僅僅只做這樣一個理解實在是太過于簡單粗陋了。另一方面,當輸出負載電容增大時,會使得Miller電容兩端所跨接的運放增益在相同頻率下變得更小,導致這個增益會在更低的頻率點下降到1。至于輸出負載電容大到多少,或者說上述增益下降到多少會另Miller補償失效,許多課程和書上并沒有給出一個很好的判斷標準,常常以“輸出電容非常大”就一帶而過了。至于說兩個極點的分離機制,Razavi和Sansen的書都只扔出了公式,沒有給出從電路原理的角度去分析這個問題的簡單方法。總之,當初在遇到問題的過程中,既沒有清晰地理解透徹Miller效應,也沒有梳理清楚Miller補償的機制,從而造成了許多困惑和不解。
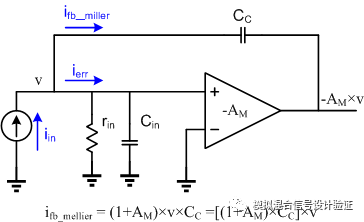
圖8
如圖8所示,Miller效應及其電容等效的原理最經典的解釋就是當輸入有一個電壓變化時,由于放大器的作用在輸出產生了一個-AM倍的電壓變化,于是在電容兩端看到了-(1+AM)倍的壓差變化,從而使得這個電容“看上去”大了(1+AM)倍,那么就相當于在輸入端等效地接了一個(1+AM)倍的電容。我們常常只關注到這個等效電容,卻忽略了流過Miller電容的電流才是問題的關鍵!從圖8中不難看出,Miller效應實質上是一種Shunt—Shunt的電壓檢測—電流反饋,我認為理解Miller效應最好的方式應該回歸到反饋的本質,去觀察各個節點電流的特性,可以獲得更豐富的內容。將一個純粹的電容與一個具有Miller效應的電容相比,之所以說等效的Miller電容要大AM倍,是由于在給定一個相同的輸入變化下,Miller電容“吃掉”的電流要大AM倍,而這個倍增的系數AM則完全由跨接在Miller電容兩端的放大器開環增益所決定。

圖9
那么再來看一下極點是如何定義的,如圖9所示,如果從電流的角度來說,極點頻率的本質實際上是指在某個節點中,讓流過電容的傳導電流模值與流過電阻的電流模值相等的頻率點。換句話說,就是隨著頻率的增加,流過電容的傳導電流增加,當頻率增加到某一個值時,流過電容的容性特征電流(電壓電流有特定的相位差)等于流過電阻的阻性電流(電壓電流同相),那么這個頻率就是所謂的極點頻率。從電流的角度來理解一下Miller極點這個概念即為什么Miller效應可以讓極點頻率低AM倍。在相同的輸入信號變化幅度跟觀察頻率下,流過Miller電容的電流會是一個純粹的電容的AM倍,那么要達到與電阻相同的電流時,Miller電容所需要的頻率自然會比一個純粹的電容小AM倍。這樣去理解Miller極點的好處是,可以很直觀的來對比各種不同接法的Miller補償間的極點位置和優缺點,比如對比Ahuja接法和電容反饋接到第一級運放輸出端的傳統接法。因為極點頻率取決于信號電流、電阻電流跟電容電流三者間模值的關系,假定信號電流的模值是固定的,那么無論是何種接法的Miller補償,在給定的頻率下,只要流過電容的反饋電流在兩種接法下保持一致或者流過電阻的誤差電流保持一致,那么兩者的極點頻率就是相等的。Ahuja接法是在第一級運放折疊點即cascode管的源極產生誤差電流,這個誤差電流流過cascode管后到達第一級運放的輸出,這個過程中電流增益“幾乎”為1,因為從第一級輸出到Miller電容另一個極板(即所接運放輸出端)間的跨阻增益在兩種接法下都是相同的,那么流過Miller電容的電流與電容反饋端產生的誤差電流之比也“幾乎”一樣。如圖10所示,因為反饋作用的存在,會使得誤差電流跟反饋電流在兩種不同的Miller補償接法下分別相等,誤差電流即流過該節點電阻的電流,那么說明兩者的極點頻率是一樣的。
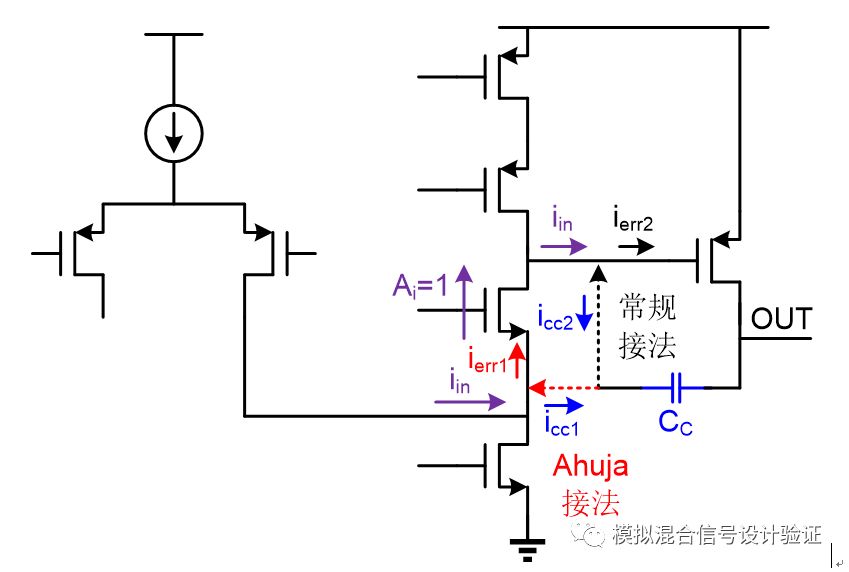
圖10
我們可以進一步做一個推論:即在保持后面跨阻不變的條件下,只要Miller電容的反饋端接到通路上等電流增益的地方,這些不同的接法所得到的Miller極點頻率是一樣的,只是Miller極點在電路上的位置不一樣(但都是在電容反饋端)。比如說在第一級運放的折疊點到第一級輸出之間插入更多的cascode管,如圖11所示,無論Miller電容的反饋端接到這兩點間所插入的任何一個cascode管的源極,所得到的Miller極點頻率是一樣的(雖然第一級運放的輸出電阻會增大從而使Miller極點頻率相比插入cascode管前要低,但是對比電容反饋端在不同的接法下是一致的)。當然,你也可以從另一個角度來理解Ahuja接法跟傳統接法兩者的等效關系,比如圖在10中,雖然Ahuja接法電容兩端看到的運放開環增益大了gm_cas×ro1倍,但是在cascode管源極看到輸出的電阻對比在第一級運放輸出端看到的輸出電阻要小ro1/(1/gm_cas)=gm_cas×ro1倍,所以兩者抵消使得極點頻率一致(gm_cas代表cascode管的跨導,ro1代表第一級運放輸出端看到的輸出電阻)。這樣的理解實際上是不那么清晰準確的,因為達到極點頻率始終取決的是相對關系而不是絕對量,隱含的條件是兩種接法在同樣的頻率使得電容電流等于電阻電流,在輸入同樣的信號電流下,他們在電流求和節點處產生的電壓由于輸出阻抗的不同而不同。
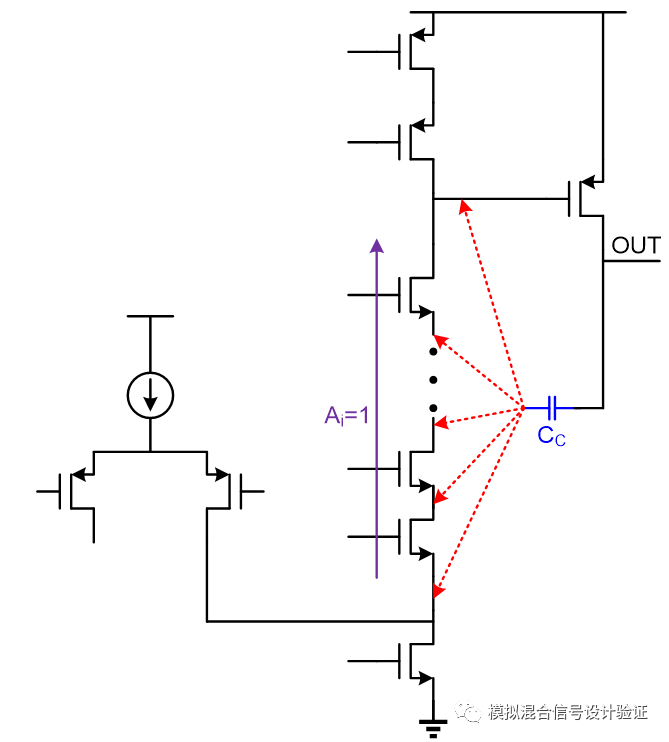
圖11
一旦從電流和反饋的角度梳理清Miller效應的原理后,你會發現一切都會變得豁然開朗。顯然,在Miller電容反饋端可能會接的一段通路上,尋找到通路上等電流增益的最前端是比較有效的Miller反饋接法,因為在保持Miller極點不變的情況下,跨接在電容兩端的電壓增益AM可能是不一樣的。例如從圖10中可以看到,相比于傳統接法,Ahuja接法的AM要大gm_cas×ro1倍,這樣會帶來兩個好處:一由于反饋和低阻點的關系讓啟動建立的過程更容易;二是對輸出極點的影響,也是我們下面想要討論的另一個問題。
我們先來看如何理解極點分離這件事情,很多Paper跟書籍會直接拋出一個公式告訴你推導一下就是這么個結論,比如Sansen書中就先給了個公式和近似條件,然后再給出一個計算結果,進而得到一個結論:“如果電路中的某個參數的改變引起了系數a的改變,兩個極點都會受到影響,朝著相反的方向移動,這就是極點分離的理論基礎”,雖然書上也給出了一張圖來描繪整個分離的軌跡過程,但是相信你看到上述文字圖片時,心里仍舊會留有一句mmp的,因為既沒有解釋“某個參數”是哪個參數,也沒有說明圖中線的斜率、間距跟拐點的意義。另一方面,雖然我們知道當輸出電容很大的時候Miller補償有可能會失效,但這個“很大”究竟是多大,有沒有什么判斷條件呢?從反饋的角度,這個問題就變得比較容易理解了:當頻率大于Miller極點頻率后,Miller電容反饋系數接近于1(假設Miller補償小環路運放輸入節點寄生電容很小),此時整個反饋環路完全建立起來,環路增益T=AM×fM,只要這個頻率下T足夠大,那么輸出等效電阻RLeq就會因為這個小環路反饋的原因而減小(1+T)倍,約為1/gmp(gmp為輸出級跨導),那么輸出極點就被推遠了(1+T)倍,這個結論在Gray書的第九章中有具體計算。因為Miller效應導致主極點低了AM倍,而輸出極點由于Miller效應被推遠了約AM倍,所以總體獲得了約AM2倍的極點分離。那么Miller補償會不會失效取決于在Miller極點頻率下所看到的小環路增益是不是遠大于1,如圖12所示可以用增益帶寬積的辦法來簡單評估多大的AM能使得分離足夠遠(假定分離前miller極點比輸出極點高了m倍),也就是分離后輸出極點至少應該比Miller極點大DC增益ATOT倍(整個運放的總增益),即AM2/m>ATOT=gm1/CC,gm1表示第一級運放輸入對的跨導,CC代表Miller電容。例如Miller電容反饋端接在第一級運放高阻輸出點的時候(輸出電阻為ro1),AM=gmpRL,m=(RLCL)/(ro1CC),所以CC>1/gmp×√((gm1×CL)/(ro1×RL)),其中RL和CL分別表示整個LDO輸出級等效電阻和負載電容。在我們的應用條件下,CL是非常非常大的,CC相比于其所接反饋節點的寄生電容也是較大的,因此后面很多分析做了一些簡化得到了一些簡單的結果,本文中如不做特殊說明則默認這樣的電容條件。當電路中這些容值的量級比較接近的時候,可以把這些特殊的結果中容值的部分用“退化”到實際電路下的等效電容值去替代就行。
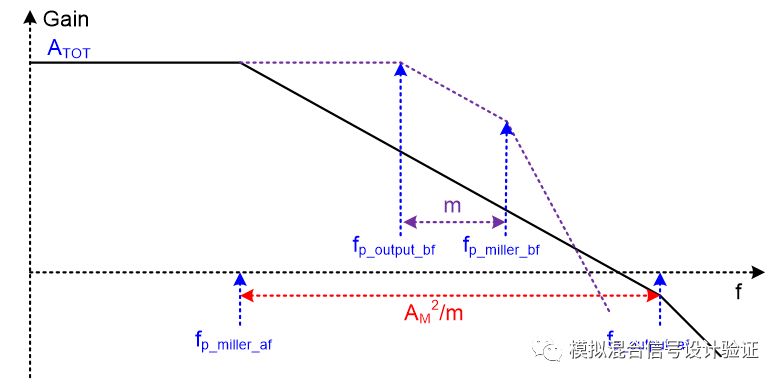
圖12
看到這里,一定會有人產生這樣一個疑問:輸出電阻因為反饋的緣故而減小了(1+T)倍,那么輸入電阻是不是也同樣的會被減小(1+T)倍呢?如此一來,豈不是輸入電阻的減小跟Miller電容的倍增相互“抵消”了?Gray并沒有給出說明,或許是他覺得這個問題太過簡單了。總之,我們知道實際中顯然不是這樣的結果,所以嘗試著做了如下的分析。
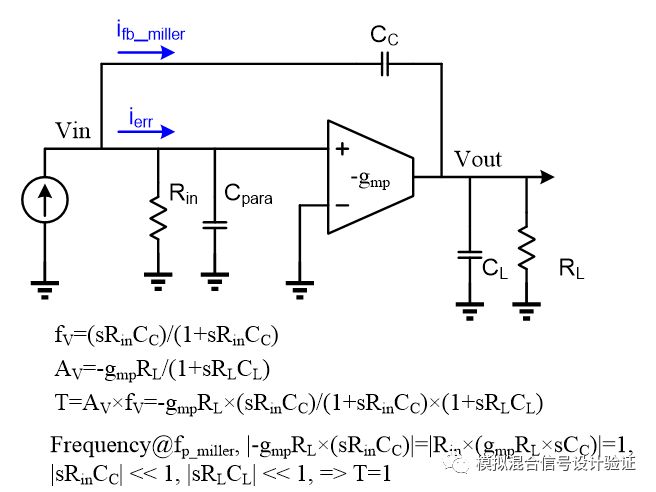
圖13
我們從低頻到高頻來仔細的捋一下Miller補償變化的整個過程:首先在低頻時,Miller電容的反饋系數是很小的,環路增益T很小,因此絕大部分的信號電流作為誤差電流流入到了運放的輸入電阻,雖然也在電容兩端產生了一個較大的壓差,但是由于頻率很低使得流過Miller電容的電流還遠小于流過輸入電阻上的電流。隨著頻率的上升,總能找到一個頻率點使得流過Miller電容的電流等于流過輸入電阻上的電流。此時雖然反饋系數很小,但環路增益T為1,因而幾乎不會降低輸入電阻,這符合原先的預期,在沒有考慮負載效應的條件下如圖13做了一個簡化的近似計算來說明環路增益T為1的情況。隨著頻率的繼續升高,流過輸入電阻的電流越來越小,輸入阻抗漸漸由輸入端寄生電容占據主導,因而反饋系數很快由于電容分壓的原因接近于1(考慮Miller電容遠大于節點寄生電容的情況),此時的環路增益T已經足夠大了,使得輸入輸出阻抗都被降低了(1+T)倍。但是,輸入阻抗降低的是容性的部分,也就是把電容增大了(1+T)倍,對于一個電流反饋系統其看進去的輸入阻抗之所以會變小,是因為在同樣大小的輸入電流信號下,大部分的電流被反饋網絡給shunt掉了而使得進入運放的電流很小產生一個很小的輸入電壓。這個被反饋網絡“吃”掉的電流是流入輸入端看到的電容中的,屬于容性成分的電流,因此這并不會改變Miller極點的位置,但卻推遠了輸出極點!輸出極點的等效阻抗被也被反饋給減小了,那為什么其s減小的是阻性阻抗而不是容性阻抗呢?首先,我們知道從輸出端的角度看過去,無論Miller電容CC還是負載電容CL都沒有因為反饋的作用而有“倍增”的效應,也就是說當輸出電壓有一個變化時,有沒有這個反饋的作用流過它們的電流是一樣的。那么所謂“由于反饋的作用減小了輸出阻抗”到底體現在什么地方呢?這其實是由于在同樣的一個電流輸入信號下,由于反饋的作用,當環路增益足夠大時,絕大部分輸入電流通過反饋網絡流到了輸出,使得輸入到運放的“誤差電流”ierr變小了(1+T)倍,從而導致輸出的電壓信號相比沒有反饋時小了(1+T)倍。等效的來說就是在“相同的輸出電壓變化下”,輸出電阻+反饋網絡“吃掉”的電流比沒有反饋時大了(1+T)倍。
雖然反饋網絡shunt的電流是容性電流,但是由于整個反饋系統先遇到的是Miller極點,所以當我們把“觀察頻率”增加到Miller極點頻率以上去尋找下一個極點時,在輸出級見到的信號電流“本身就應該”是一個容性電流,也就是說Miller電容所在的反饋網絡從輸入端shunt過來的容性電流是和信號電流保持一致的。我們可以從另一個角度再來理解一下,即當頻率高過Miller極點之后,輸入端流入容性部分的電流相比于流入阻性部分的電流會越來越多,使得流入系統的輸入電壓信號跟電流的相位關系越來越表現出“電容性質的相位關系”,那么如果在系統輸出端也展現出這樣的相位關系,則表明放大器和反饋網絡所組成的整體表現出了阻性的特征(保持輸入輸出電壓電流相位關系不變)。也就是說反饋使得在輸出端所看到阻抗的整個等效的阻性部分變小了,從而推遠了輸出極點。
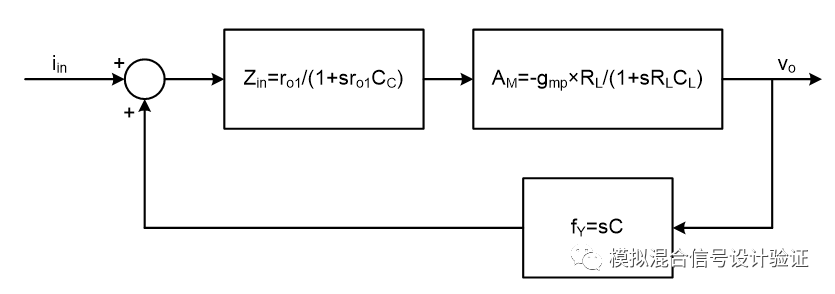
圖14
圖13只是一個非常簡化近似的計算用來舉例說明Miller極點跟輸出極點隨補償的變化,下面從系統拓撲的角度來詳細分析一下,如圖13這樣一個帶有Miller電容補償的系統結構可以用圖14中的拓撲來表示。其中ro1代表圖中輸入電阻Rin可以看作是運放的輸入電阻,假設Cpara相比CC很小可以忽略,所以系統看進去的考慮到了反饋網絡負載影響后的開環輸入阻抗Zin是輸入電阻跟電容CC的并聯。
如果我們僅僅想從輸入電壓到輸出電壓的角度來看系統前向AV和反饋網絡對極點分離的作用,那么我們可以做一個簡單的變換得到如圖15的拓撲。
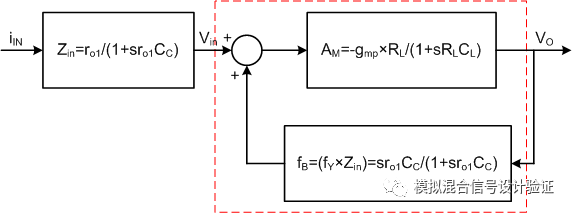
圖15
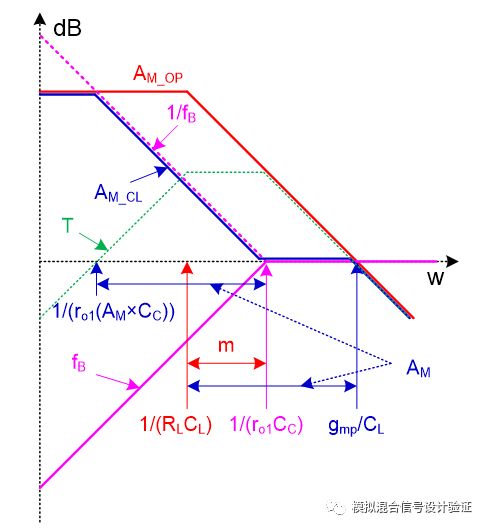
圖16
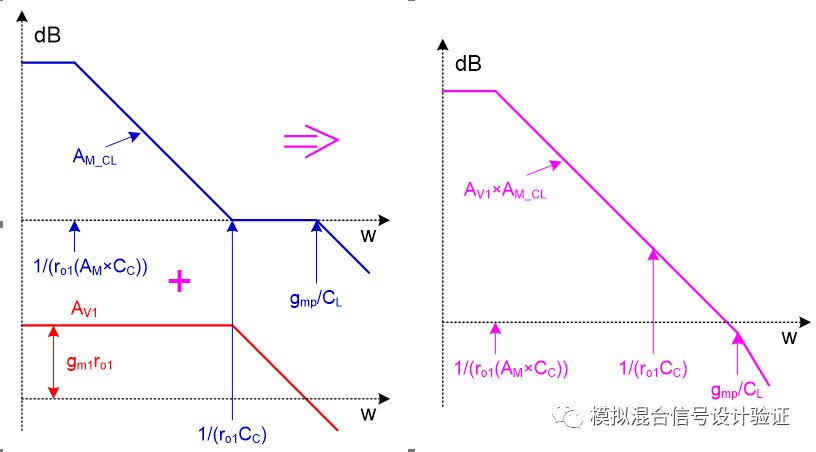
俗話說千言萬語不如一張圖,我們可以將圖15中的各個部分如運放開環電壓增益AM、反饋網絡電壓增益fB、其倒數1/fB、環路增益T=AM×fB還有圖中紅框里整個系統的閉環增益等參量隨頻率變化的曲線都描繪在一起,并將它們結合起來,最終可以得到Miller補償小環路的一個近似的傳遞函數曲線,如圖16所示。
圖中紅色AM_OP代表跨接在Miller電容兩端的運放開環增益曲線,AM代表其DC值;紫色fB表示反饋網絡的增益曲線;綠色的T代表圖15中紅框所包含系統的環路增益曲線;藍色AM_CL表示的就是圖15中紅框所包含系統的閉環增益曲線。圖16中線條較多有些復雜,不過如果能將所有線條、拐點、斜率的意義搞明白,那么Miller效應和Miller補償也就能理解的差不多了。從圖中不難看出,環路增益T在Miller極點處超過1,又在被推遠了的輸出極點處回落到1,整個閉環系統在T遠大于1時的中間部分follow曲線1/fB,在兩頭T遠小于1時follow曲線AM_OP。所以,藍色的閉環增益曲線具有兩個極點,分別是補償后的Miller主極點和在單位增益處的被推遠了的輸出次極點,整條曲線展現出的是一個“形似”積分器的形式,低頻時候受限運放增益,主極點后增益單調下降直到單位增益,次級點后增益繼續下降(因為只是為了觀察圖15中紅色框里系統的特性沒有將輸入阻抗Zin考慮進來因而相比真正的積分器曲線有一段增益為1的平臺)。從圖中我們可以清晰的看到兩個極點分離的情況,同時也可以印證,在斷開環路做仿真時,應該保持這個帶有Miller電容的補償小環路的完整性,也就是因為反饋的原因其閉環特性需要被整體來看待。兩極點最終分離之后的距離為AM2/m,試想一下將粉色反饋網絡增益曲線左右移動一下,不難發現其中還隱含著Miller補償失效的條件為m>AM,即ro1CC
當然圖16也只是一個簡化的分析,有許多未考慮的因素,比如沒有把反饋節點處的寄生電容跟輸出負載電容受反饋網絡影響的情況計算進去,比如忽略了其他較遠的次級點,并且也沒能解釋實際中為什么增大CC可以將次級點推得更遠(這是因為從負載端看到的等效電容還需要把帶有CC的反饋網絡看進去的等效電容給考慮進去,如CC串聯Cin_para后與CL并聯,這里因為CL非常大而做了簡化),當然本例中能看到次級點被推遠的極限為gmp/CL,這還決定了整個LDO最大能夠做到的帶寬。我們還可以進一步把前面的輸入阻抗Zin和前級的gm1都考慮進來,把gm1×Zin當成一個整體看作是前級運放的開環增益,得到如圖17所示的拓撲結構,同時也可以在圖16的基礎上繪制出帶Miller補償的兩級運放的整個前向通路的增益曲線,如圖18所示,這基本上就是一個積分器的樣子了(如果有興趣的話還可以嘗試著畫一下無源RC濾波電路和有源RC濾波器的波特圖)。
圖17
圖18
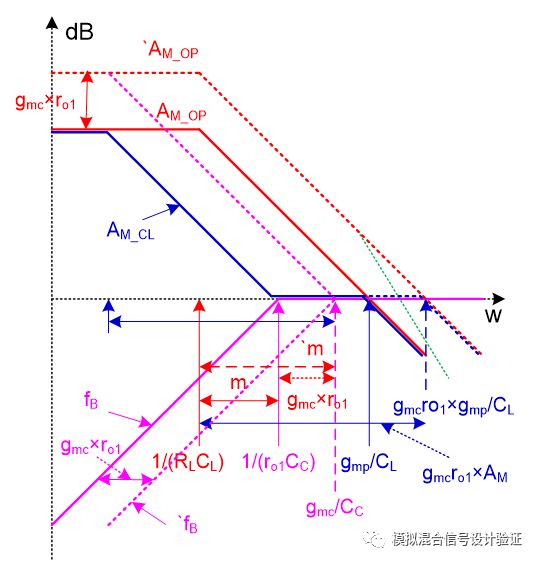
圖19
從圖16出發,我們可以更進一步的來分析對比Ahuja接法的Miller補償跟常規接法的Miller補償,如圖19所示。相對于常規接法,Ahuja接法由于電容反饋點從第一級運放輸出移到了第一級運放的折疊端cascode管源極,所以跨接在電容兩端的運放增益相比要大gmc×ro1倍。其中gmc表示cascode管跨導,ro1則代表了第一級運放的輸出端電阻(上下兩個cascode結構輸出阻抗的并聯),因為兩個節點之間電流增益為1,所以可以知道cascode管源端的輸出電阻要小gmc×ro1倍,那么從圖中可以看到反饋網絡的零點右移了gmc×ro1倍,從粉色實線變為了粉色虛線,同理可推其他曲線的變化,最終可以看到Miller極點的位置并沒有發生改變,而輸出次級點被推得更遠了。至此,我們可以很清楚的理解到Ahuja接法的優勢,因為Miller補償所在環路的運放開環增益AM相比傳統接法大了gmc×ro1倍,雖然圖中m值也大了這么多倍,但分離后的距離為AM2/m,總體變大了gmc×ro1倍,這是由于輸出極點相比被推的更遠了!
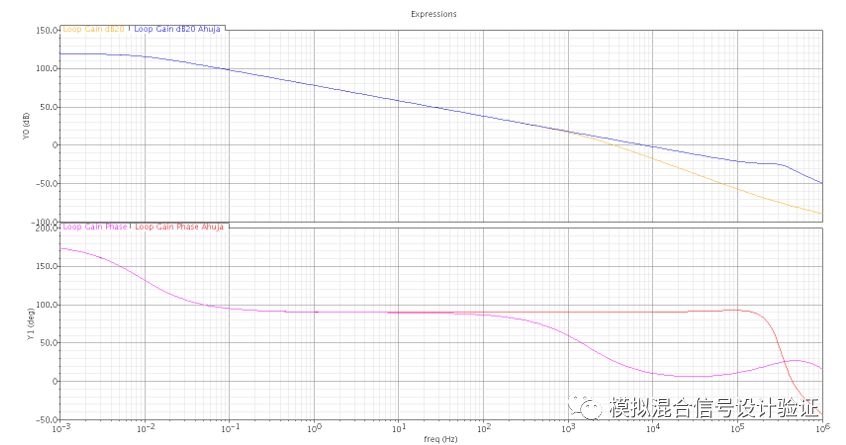
同樣,我們也可以把前面的輸入阻抗Zin和前級跨導gm1包含進來,就可以繪出類似于圖18右側這樣的曲線,只是其次級點會被推得更遠,這里不再累述,具體的仿真結果對比如圖20所示。這里會衍生出一個問題:是不是只要往跨接在Miller電容兩端的電路中間不斷插入更多的cascode管就可以一直將補償后的單位增益帶寬推得更遠呢?這顯然是不行的,因為級聯不斷增加的cascode結構會在其最后一個MOS管的漏端產生一個很大的輸出端阻抗引入到AM中從而使其在單位增益帶寬前不再保持單極點曲線,如圖19中綠線所示那樣,那么就有可能影響次級點被推遠的距離、帶寬跟穩定性。為了讓AM不引入太大的次級點,中間插入多個單級運放可能是更好的選擇,因此我猜測Nested Miller補償大概是基于這樣的考慮吧,類似于多級級聯的Buffer電路意圖以此合理分配不同級間的驅動能力,本文里對Miller效應和補償的一些思考相信可以對理解Nested Miller補償有所幫助,但是具體的原理應該還是需要從Huijsing的書中去尋找答案。
圖20
通過上述深入的剖析,我們可以發現從電流和反饋的角度能夠更好的理解Miller效應和Miller補償,同時也獲得了一些直觀的認識和結論:1.仿真分析在斷開環路時應盡量保持Miller補償所在小環路的完整性,因為嵌套的內部閉環會對其輸入輸出阻抗產生影響,同時盡可能把斷點設置在純系數反饋的位置;2.Miller等效的輸入電容是由跨接在其兩端的運放開環增益所決定的;3.只要保持后面的跨阻一致,把Miller電容的反饋端接到跨阻前的這段通路的任何等電流增益位置,都能獲得一樣的Miller極點頻率;4.輸出極點因為Miller反饋的作用被推遠了(1+T)倍,可以從增益帶寬積的角度結合圖12或圖16來推算有效的極點分離需要多大的Miller電容和補償小環路里多大的環路增益T,判斷是不是一定可以補償的了,在什么條件下會失效;5.Ahuja接法優點多多,暫時沒有看到明顯的缺點;6.通過Shift一個DC電壓(比如用源極跟隨器)并配合反饋系數的放大或縮小,可以將Miller電容的兩端都放到合適的電壓域,通過阻抗變換(還比如插入一個源極跟隨器),可以隔離Miller電容的前饋效應,或者說僅引入反饋或僅引入前饋。7.可以嘗試利用這些關于單個Miller反饋的思考來進一步幫助分析和簡化Nested Miller補償的原理,比如把嵌套在最里面的Miller環路作為一個整體的積分器,像圖16和圖18一樣,一步步地“組合”出最終整個前向通路的增益曲線。
至此,雖然還不能說已經將Miller補償完全搞懂了,但是通過一些有意義的思考還是能有效的幫助我們看清其中的一些門道,并在具體實踐中提供一些有用的判據和簡化計算的結果。雖然整個過程有點燒腦,但花了幾個夜晚最終寫出這些文字的時候感覺還是非常值得的!最后,還要感謝我的同事江文平、馬吉和金津所提供的熱情的幫助、探討和給予的建議!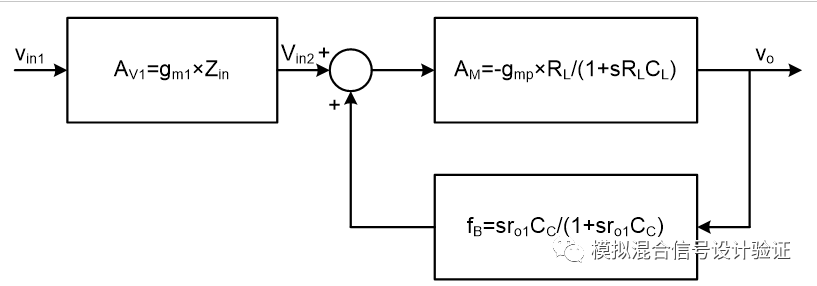
-
ldo
+關注
關注
35文章
2295瀏覽量
155918 -
補償
+關注
關注
1文章
107瀏覽量
19930 -
大電容
+關注
關注
0文章
12瀏覽量
8622
原文標題:一次錯誤的仿真所引發的血案——對Miller效應及補償的重新思考
文章出處:【微信號:all4lib,微信公眾號:開源Block】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
音頻信號采集為什么要用專用的CODEC來實現,普通高精度高采樣率ADC可以嗎?
[最新資料]給各位推薦一個超高精度,帶過溫保護的45W降壓恒流驅動器方案!
[最新資料]給各位推薦一個超高精度的,帶過溫保護的,45W降壓恒流驅動器方案!
基于LDO穩壓器的帶隙基準電壓源設計
高精度高穩定功率測量技術
UC3842 Boost開關電源電壓調整率和負載調整率很差
國際一流寬電壓高精度響應快OC4001升降壓恒流方案
電源的負載調整率怎么提高?
國巨高精度高容值貼片電容有哪些?






 高精度高負載調整率帶片外大電容的LDO也可以使用Miller補償嗎?
高精度高負載調整率帶片外大電容的LDO也可以使用Miller補償嗎?










評論