以下文章來源于瘋狂的FPGA,作者CrazyFPGA
前面發過中值、均值、高斯濾波的文章,這些只考慮了位置,并沒有考慮相似度。那么雙邊濾波來了,既考慮了位置,有考慮了相似度,對邊緣的保持比前幾個好很多,當然實現上也是復雜很多。本文將從原理入手,采用Matlab與FPGA設計實現雙邊濾波算法。
1.雙邊波算法的實現
濾波算法的基本思路,就是采用周邊像素,加權平均計算一個新的像素,來緩減噪聲對當前像素的影響。我們已經介紹了均值濾波,中值濾波,高斯濾波算法。但這幾種算法都不夠完美,還有繼續提升的空間:
1)均值濾波:簡單粗暴的將窗口內的像素累加后求均值,將噪聲平均化,同時邊緣紋理也被抹平了,有模糊的作用,作為入門學習用。
2)中值濾波:采用窗口內中值的方法,有效剔除了異常高亮或過暗的噪聲,對椒鹽噪聲的去除效果比較好,但實際的圖像會伴隨著邊緣紋理,由于只考慮中值,也會將圖像細節去除,只是比均值濾波稍微好一點而已。
3)高斯濾波:采用歐氏距離,權重呈正態分布,相比均值/中值更優,因為均值/中值權重未考慮距離因素,而高斯噪聲則考慮了噪聲相對當前像素,呈高斯分布的特性,效果更佳。但高斯濾波也只是考慮了距離,未考慮邊緣紋理,對細節的保護仍然不佳。
那么,既考慮噪聲高斯分布特性,由將圖像邊緣紋理考慮進去的濾波算法應運而生。這里我們提出更進一步的濾波—雙邊濾波。
我們這里在前面高斯濾波的基礎上,追加實現雙邊濾波,計劃采用3*3的窗口,高斯濾波權重直接采用上一節的代碼生成,重點講解如何進行權重的計算,及Matlab&FPGA的實現。
1.1.高斯濾波算法理論
雙邊濾波是一種非線性濾波器,它可以達到降噪平滑,同時又保持邊緣的效果。和其他濾波原理一樣,雙邊濾波也是采用加權平均的方法,用周邊像素亮度值的加權平均,來代表某個像素的強度,所用的加權平均也是基于高斯分布。
這里雙邊濾波的權重,不僅考慮了像素的歐式距離(如高斯濾波),還考慮了像素范圍的輻射差異(比如像素與中心像素之間相似程度,也是高斯分布的),結合距離與相似度,最終計算得到最終的權重(距離與相似度的高斯分布)。
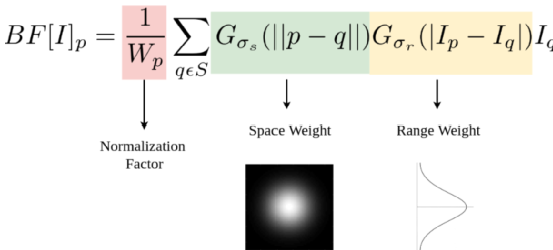
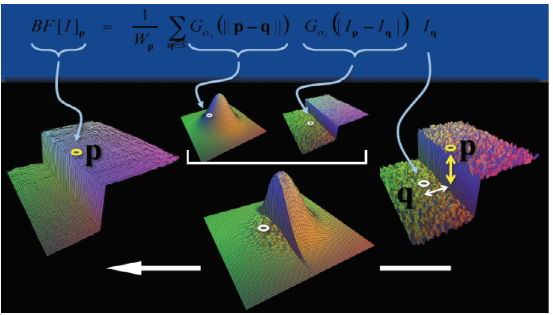
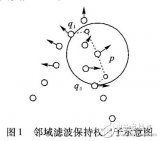
引用雙邊濾波算法相關圖解,如下所示,其中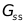 為只考慮與當前像素空間距離的權重(space weight),而
為只考慮與當前像素空間距離的權重(space weight),而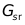 則為只考慮和當前像素相似度的權重(range weight),最后相乘,得到
則為只考慮和當前像素相似度的權重(range weight),最后相乘,得到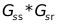 則為同時考慮了距離與相似度的權重,公式累加后最后歸一化,得到最終的權重(space & rang)。
則為同時考慮了距離與相似度的權重,公式累加后最后歸一化,得到最終的權重(space & rang)。
由于雙邊濾波同時考慮了空間距離和像素相似度的影響,因此尤其在具有邊緣梯度的圖像中,能夠有不錯的效果。即在平坦區域,空間距離占優勢,在邊緣區域,像素間相似度占優勢,可以直觀的用下面這個圖來表示(注明出處):
上述公式太抽象,我們進一步細化,并重新梳理如下。其中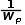 為歸一化因子,高斯分布參數
為歸一化因子,高斯分布參數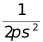 由于最終需要歸一化,就直接省略了:
由于最終需要歸一化,就直接省略了:
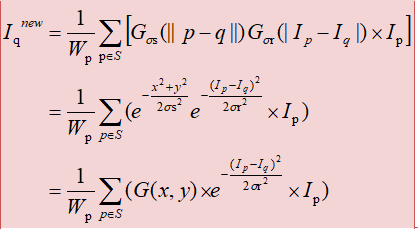
從公式可知,對于給定的窗口大小(比如3*3),以及確定的方差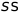 、
、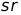 ,
,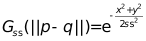 為常數,可以提前計算好高斯模板,具體的計算方式在高斯濾波中已經給出,以3*3窗口,
為常數,可以提前計算好高斯模板,具體的計算方式在高斯濾波中已經給出,以3*3窗口,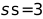 為例,采用Data_Generate_nxn.m生成模板,如下所示(擴大了1024倍后):
為例,采用Data_Generate_nxn.m生成模板,如下所示(擴大了1024倍后):
因此接下來需重點處理的是相似度權重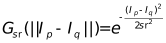 ,這也是我們Matlab與FPGA RTL實現的重點了。
,這也是我們Matlab與FPGA RTL實現的重點了。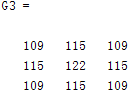
1.2.雙邊濾波Matlab實現
1.2.1.浮點雙邊濾波實現
首先,以3*3窗口,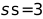 為例,采用Data_Generate_nxn.m生成3*3高斯模板定點化后的結果,相關代碼及生成的數據過程如下所示(擴大了1024倍后):
為例,采用Data_Generate_nxn.m生成3*3高斯模板定點化后的結果,相關代碼及生成的數據過程如下所示(擴大了1024倍后):
最終得到的G3高斯模板為定點化后的結果,因此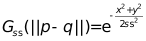 就不需要再計算,接下來只需要關心相似度權重即可,即
就不需要再計算,接下來只需要關心相似度權重即可,即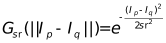 的計算。針對灰度圖像的權重計算,先計算當前像素的相似度分布權重,再計算最終的雙邊濾波,相關核心Matlab代碼如下所示:
的計算。針對灰度圖像的權重計算,先計算當前像素的相似度分布權重,再計算最終的雙邊濾波,相關核心Matlab代碼如下所示:

這里套用的仍然是我們濾波窗口處理的Matlab相關代碼,以3*3為例,具體解釋如下:
1)42行:獲取以當前像素為中心的n*n的圖像窗口A;
2)44行:計算以當前像素為中心的n*n窗口內的相似度權重;
3)45行:將高斯權重與相似度權重點乘,得到同時考慮距離與相似度的雙邊濾波權重;
4)46行:歸一化雙邊濾波權重;
5)47行:當前窗口與雙邊濾波權重卷積,累加后得到最終的結果。
這里44、45行是最重要的地方,最終結果就是完成上面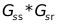 的計算結果。我們驗證一下效果如何,如下所示,左圖為原圖,右圖為3*3窗口,sigma_d = 3, sigma_r = 0.1的濾波結果:
的計算結果。我們驗證一下效果如何,如下所示,左圖為原圖,右圖為3*3窗口,sigma_d = 3, sigma_r = 0.1的濾波結果:
最后我們封裝function便于調用,再給出完整的代碼。如下所示。這里的sigma_d就是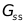 ,而sigma_r即是
,而sigma_r即是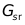 。 ?
。 ?
% 灰度圖像雙邊濾波算法實現
% I為輸入的灰度圖像
% n為濾波的窗口大小,為奇數
function B=bilateral_filter_gray(I,n,sigma_d, sigma_r)
% ---------------------------------------------------
% 僅供function自測使用
% clear all; close all;clc;
% I = rgb2gray(imread('../../images/Scart.jpg')); % 讀取jpg圖像
% n = 3; sigma_d = 3; sigma_r = 0.1;
dim = size(I); %讀取圖像高度、寬度
w=floor(n/2); %窗口 [-w, w]
% ---------------------------------------------------
% 計算n*n高斯模板
G1=zeros(n,n); %n*n高斯模板
for i=-w : w
forj=-w : w
G1(i+w+1,j+w+1) = exp(-(i^2 + j^2)/(2*sigma_d^2)) ;
end
end
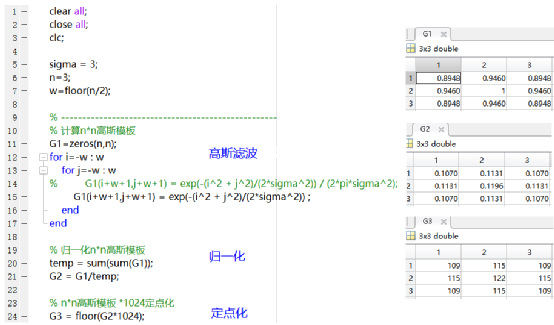
% 歸一化n*n高斯濾波模板
temp = sum(G1(:));
G2 = G1/temp;
% n*n高斯模板 *1024定點化
G3 = floor(G2*1024);
I = double(I);
% ---------------------------------------------------
% 計算n*n雙邊濾波模板+ 濾波結果
h = waitbar(0,'Speed of bilateral filter process...');%創建進度條
B = zeros(dim);
for i=1 : dim(1)
forj=1 : dim(2)
if(i
B(i,j)= I(i,j); %邊緣像素取原值
else
A= I(i-w:i+w, j-w:j+w);
% H =exp( -(I(i,j)-A).^2/(2*sigma_r^2)) ;
H= exp( -((A-I(i,j))/255).^2/(2*sigma_r^2));
F= G3.*H;
F2=F/sum(F(:));
B(i,j)= sum(F2(:) .*A(:));
end
end
waitbar(i/dim(1));
end
close(h); % Close waitbar.
I = uint8(I);
B = uint8(B);
% ---------------------------------------------------
% 僅供function自測使用
% subplot(121);imshow(I);title('【1】原始圖像');
% subplot(122);imshow(B);title('【2】雙邊濾波結果');
我們進一步進行測試,與遷移章中的高斯濾波,在相同窗口,及sigma_d下進行對比,相關代碼及結果如下所示(Bilateral_Filter_Test1.m):
clear all;
close all;
clc;
% -------------------------------------------------------------------------
% Read PC image to Matlab
% IMG1= imread('../../images/Lenna.jpg'); % 讀取jpg圖像
IMG1= imread('../../images/Scart.jpg'); % 讀取jpg圖像
IMG1 = rgb2gray(IMG1);
h = size(IMG1,1); % 讀取圖像高度
w = size(IMG1,2); % 讀取圖像寬度
imshow(IMG1);title('【1】原圖');
% -------------------------------------------------------------------------
figure;
% -------------------------------------------------------------------------
IMG2 = imfilter(IMG1, fspecial('gaussian',[3,3],1), 'replicate');
IMG3 = imfilter(IMG1, fspecial('gaussian',[3,3],2), 'replicate');
IMG4 = imfilter(IMG1, fspecial('gaussian',[5,5],3), 'replicate');
subplot(231);imshow(IMG2);title('【1】高斯濾波3*3, sigma = 1');
subplot(232);imshow(IMG3);title('【2】高斯濾波3*3, sigma = 2');
subplot(233);imshow(IMG4);title('【3】高斯濾波5*5, sigma = 3');
% -------------------------------------------------------------------------
IMG6 = bilateral_filter_gray(IMG1, 3, 1, 0.1);
IMG7 = bilateral_filter_gray(IMG1, 3, 2, 0.3);
IMG8 = bilateral_filter_gray(IMG1, 5, 3, 0.8);
subplot(234);imshow(IMG6);title('【4】雙邊濾波3*3, sigma = [1, 0.1]');
subplot(235);imshow(IMG7);title('【5】雙邊濾波3*3, sigma = [2, 0.3]');
subplot(236);imshow(IMG8);title('【6】雙邊濾波5*5, sigma = [3, 0.8]');
如上圖所示,第一行為高斯濾波,第二行為雙邊濾波,不難發現,雙邊濾波對邊緣的保護成都更好。那么邊緣濾波的3個參數:n、sigma_d、sigma_r對雙邊濾波強度的影響程度如何,我們進一步分析。
相關代碼詳見Bilateral_Filter_Test2.m首先是sigma_d,如下所示,可見濾波強度類似,sigma_d對雙邊權重的影響并不大。
其次是sigma_r,同時3*3窗口,sigma_d=3下對比,如下所示:
最后進行濾波窗口系數n的測試,磨皮的效果出來了,可見對濾波強度的影響最大。
綜上,感性的分析,對濾波強度的影響,首先是濾波窗口,其次是sigma_r,最后才是sigma_d。所以固定窗口下,sigma_r有較大的權重,也正是因此,相似度是雙邊權重的一個重要因素,當相似度高時,則權重收距離的影響更大;反之則收到相似度影響更大,因此也能有效地保護邊緣,這就是雙邊濾波。
1.2.2. 定點雙邊濾波實現
我們的目標是FPGA實現,但上述結Matlab計算中,主要是相似度權重計算中,仍然有浮點的參與。主要涉及公式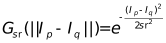 ,這里不難看出,相鄰2像素的插值的絕對值,一定∈[0,255],那么我們可以提前計算好
,這里不難看出,相鄰2像素的插值的絕對值,一定∈[0,255],那么我們可以提前計算好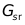 并定點化,那么就可以用查找表的方法來實現相似度權重的計算了。相關代碼如下所示: ?
并定點化,那么就可以用查找表的方法來實現相似度權重的計算了。相關代碼如下所示: ?
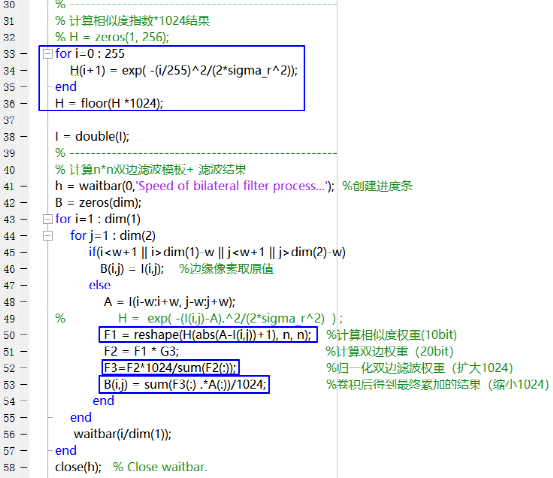
其中框框部分較為重要,詳解如下:
1)第一個框:實現的是0-255下,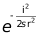 的查找表,同時為了避免出現浮點,將結果擴大了1024倍。
的查找表,同時為了避免出現浮點,將結果擴大了1024倍。
2)第二個框:根據查找表H,實現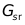 的計算,其結果位寬為10bit;
的計算,其結果位寬為10bit;
3)第三個框:仍然將F2擴大1024倍后再運算,防止歸一化出現浮點;
4)第四個框:將結果縮小1024倍,得到最終8bit的計算結果。
這樣采用查找表的方式,我們不僅避免了指數的運算,同時也避免了浮點的運算,那么得到了定點化的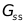 與
與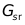 ,后續的計算都不在話下了。這是FPGA實現時通用的定點化方法,也是本文后續的實現方式。
,后續的計算都不在話下了。這是FPGA實現時通用的定點化方法,也是本文后續的實現方式。
再次封裝我們的函數,bilateral_filter_gray_INT(I,n,sigma_d, sigma_r),增加“_INT”與bilateral_filter_gray區分,Matlab代碼如下所示:
% 灰度圖像雙邊濾波算法實現
% I為輸入的灰度圖像
% n為濾波的窗口大小,為奇數
function B=bilateral_filter_gray_INT(I,n,sigma_d, sigma_r)
% clear all; close all;clc;
% I = rgb2gray(imread('../../images/Scart.jpg')); % 讀取jpg圖像
% n = 3; sigma_d = 3; sigma_r = 0.1;
dim = size(I); %讀取圖像高度、寬度
w=floor(n/2); %窗口 [-w, w]
% ---------------------------------------------------
% 計算n*n高斯模板
G1=zeros(n,n); %n*n高斯模板
for i=-w : w
forj=-w : w
G1(i+w+1,j+w+1) = exp(-(i^2 + j^2)/(2*sigma_d^2)) ;
end
end
% 歸一化n*n高斯濾波模板
temp = sum(G1(:));
G2 = G1/temp;
% n*n高斯模板 *1024定點化
G3 = floor(G2*1024);
% ---------------------------------------------------
% 計算相似度指數*1024結果
% H = zeros(1, 256);
for i=0 : 255
H(i+1)= exp( -(i/255)^2/(2*sigma_r^2));
end
H = floor(H *1024);
I = double(I);
% ---------------------------------------------------
% 計算n*n雙邊濾波模板+ 濾波結果
h = waitbar(0,'Speed of bilateral filter process...');%創建進度條
B = zeros(dim);
for i=1 : dim(1)
forj=1 : dim(2)
if(i
B(i,j)= I(i,j); %邊緣像素取原值
else
A= I(i-w:i+w, j-w:j+w);
% H =exp( -(I(i,j)-A).^2/(2*sigma_r^2)) ;
F1= reshape(H(abs(A-I(i,j))+1), n, n); %計算相似度權重(10bit)
F2= F1 * G3; %計算雙邊權重(20bit)
F3=F2*1024/sum(F2(:)); %歸一化雙邊濾波權重(擴大1024)
B(i,j)= sum(F3(:) .*A(:))/1024; %卷積后得到最終累加的結果(縮小1024)
end
end
waitbar(i/dim(1));
end
close(h); % Close waitbar.
I = uint8(I);
B = uint8(B);
% subplot(121);imshow(I);title('【1】原始圖像');
% subplot(122);imshow(B);title('【2】雙邊濾波結果');
調用如上函數,與bilteral_Filter_gray函數進行對比,顯示結果一致,驗證了我們的改進結果,是符合預期的。
最后,經常說雙邊濾波是一種磨皮算法,即去掉了斑紋又保持了邊緣,那我們不妨找一個美女的頭像測試一下,如下所示,為帶噪聲的神奇女俠(蓋爾.加朵),在3*3窗口,sigma_d=3, sigma_r=0.1下的雙邊濾波效果。可見噪聲被去除了,皮膚也變得光滑了,而且邊緣紋理得以保留了。
這里處理的是彩色圖像的雙邊濾波,需要RGB三通道,而我們的bilateral_filter_gray_INT()為灰度處理的函數,因此分3次分別處理了3個通道的數據,相關代碼如下所示。當然也可以另行設計支持彩色圖像的雙邊濾波函數,這個請讀者自己努力,加油!
clear all;
close all;
clc;
% -------------------------------------------------------------------------
% Read PC image to Matlab
IMG1= imread('../../images/girl.jpg'); % 讀取jpg圖像
% -------------------------------------------------------------------------
subplot(121);imshow(IMG1);title('【1】原圖');
IMG2(:,:,1) = bilateral_filter_gray_INT(IMG1(:,:,1), 3, 3, 0.1);
IMG2(:,:,2) = bilateral_filter_gray_INT(IMG1(:,:,2), 3, 3, 0.1);
IMG2(:,:,3) = bilateral_filter_gray_INT(IMG1(:,:,3), 3, 3, 0.1);
subplot(122);imshow(IMG2);title('【2】雙邊濾波3*3, sigma = [3, 0.1]');
1.3.雙邊濾波FPGA實現
我們整理上一節中高斯模板與相似度查找表的生成代碼,文件名:Data_Generate_nxn_BF.m,Matlab代碼如下所示。
clear all;
close all;
clc;
sigma_d = 3; sigma_r=0.1;
n=3;
w=floor(n/2);
% ---------------------------------------------------
% 計算n*n高斯模板
G1=zeros(n,n);
for i=-w : w
forj=-w : w
G1(i+w+1,j+w+1) = exp(-(i^2 + j^2)/(2*sigma_d^2)) ;
end
end
% 歸一化n*n高斯模板
temp = sum(sum(G1));
G2 = G1/temp;
% n*n高斯模板 *1024定點化
G3 = floor(G2*1024);
% ---------------------------------------------------
% 計算相似度指數*1024結果
H = zeros(1, 256);
for i=0 : 255
H(i+1)= exp( -(i/255)^2/(2*sigma_r^2));
end
H = floor(H *1024);
這里采用3*3的窗口,sigma_d=3, sigma_r=0.3的強度為例,高斯權重生成的數據如下所示:
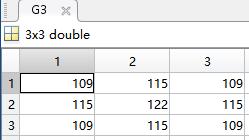
而相似度查找表直接寫入verilog文件,相關代碼如下所示(詳見Data_Generate_nxn_BF.m):
% ----------------------------------------------------------------------
fp_gray = fopen('.Similary_LUT.v','w');
fprintf(fp_gray,'//Sigma_r = %d ', sigma_r);
fprintf(fp_gray,'module Similary_LUT ');
fprintf(fp_gray,'( ');
fprintf(fp_gray,' input [7:0] Pre_Data, ');
fprintf(fp_gray,' output reg [9:0] Post_Data ');
fprintf(fp_gray,'); ');
fprintf(fp_gray,'always@(*) ');
fprintf(fp_gray,'begin ');
fprintf(fp_gray,' case(Pre_Data) ');
% -----------------------------
% 計算相似度指數*1024結果
Similary_ARRAY = zeros(1,256);
for i = 0 : 255
temp= exp( -(i/255)^2/(2*sigma_r^2));
if(temp== 1) %i=0
Similary_ARRAY(i+1)= 1023;
else
Similary_ARRAY(i+1)= floor(temp*1023);
end
fprintf(fp_gray,' 8''d%03d: Post_Data = 10''d%d; ',i, Similary_ARRAY(i+1) );
end
fprintf(fp_gray,' endcase ');
fprintf(fp_gray,'end ');
fprintf(fp_gray,' endmodule ');
fclose(fp_gray);
這里特別需要注意的是,為了最后的映射的數據保證10bit位寬(方便FPGA RTL設計),當Similary_ARRAY(i)=1時,其結果取1023,而非1024。
執行后生成Similar_LUT.v,完成查找表的映射,文件代碼如下,該文件可直接用于sigma_r下exp指數的運算。
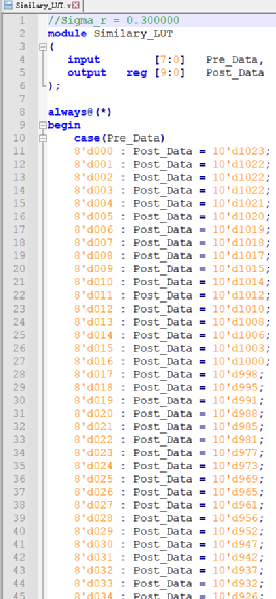
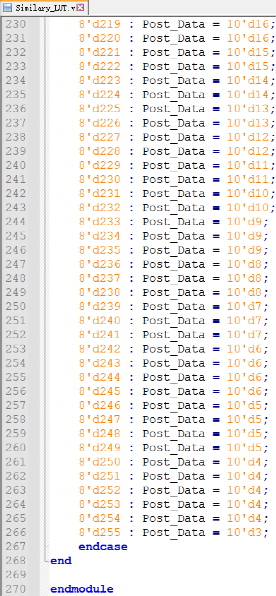
-
FPGA
+關注
關注
1645文章
22034瀏覽量
617892 -
matlab
+關注
關注
189文章
3001瀏覽量
233996 -
濾波算法
+關注
關注
2文章
90瀏覽量
13955
原文標題:基于Matlab與FPGA的雙邊濾波算法實現
文章出處:【微信號:HXSLH1010101010,微信公眾號:FPGA技術江湖】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
基于FPGA的中值濾波算法實現
介紹幾種嵌入式常用濾波算法的matlab實現
高階QAM定時同步算法的MATLAB仿真及FPGA實現
雙邊濾波原理_HLS實現Bilateral Filtering雙邊濾波器
matlab實現的自適應濾波算法
雙邊濾波點云去噪算法





 基于Matlab與FPGA的雙邊濾波算法實現
基于Matlab與FPGA的雙邊濾波算法實現












評論