1 BP神經網絡概述
BP 神經網絡是一類基于誤差逆向傳播 (BackPropagation, 簡稱 BP) 算法的多層前饋神經網絡,BP算法是迄今最成功的神經網絡學習算法。現實任務中使用神經網絡時,大多是在使用 BP 算法進行訓練。值得指出的是,BP算法不僅可用于多層前饋神經網絡,還可以用于其他類型的神經網絡,例如訓練遞歸神經網絡。但我們通常說 “BP 網絡” 時,一般是指用 BP 算法訓練的多層前饋神經網絡。
2 神經網絡的前饋過程

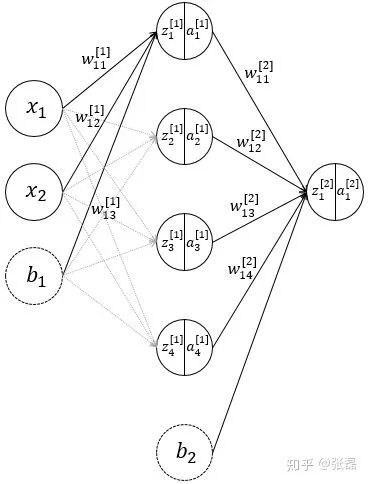
神經網絡結構示意圖
上述過程,即為該神經網絡的前饋 (forward propagation) 過程,前饋過程也非常容易理解,符合人正常的邏輯,具體的矩陣計算表達如
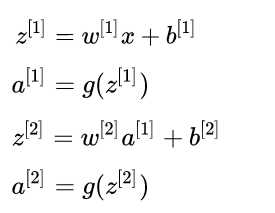
3 逆向誤差傳播 (BP過程)

我們的任務就是:給定了一組數據集,其中包含了輸入數據和輸出的真實結果,如何尋找一組最佳的神經網絡參數,使得網絡計算得到的推測值能夠與真實值吻合程度最高?
3.1 模型的損失函數
為了達到這個目標,這也就轉換為了一個優化過程,對于任何優化問題,總是會有一個目標函數 (objective function),在機器學習的問題中,通常我們稱此類函數為:損失函數 (loss function),具體來說,損失函數表達了推測值與真實值之間的誤差。抽象來看,如果把模型的推測以函數形式表達為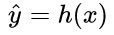 ?(這里的函數字母使用 h 是源于“假設 hypothesis“ 這一單詞),對于有m個訓練樣本的輸入數據而言,其損失函數則可表達為:
?(這里的函數字母使用 h 是源于“假設 hypothesis“ 這一單詞),對于有m個訓練樣本的輸入數據而言,其損失函數則可表達為:
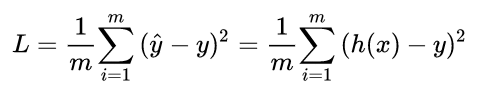
那么在該問題中的損失函數是什么樣的呢?拋開線性組合函數,我們先著眼于最終的激活函數,也就是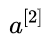 的值,由于 sigmoid 函數具有很好的函數性質,其值域介于 0 到 1 之間,當自變量很大時,趨向于 1,很小時趨向于 0,因此,該模型的損失函數可以定義如下:
的值,由于 sigmoid 函數具有很好的函數性質,其值域介于 0 到 1 之間,當自變量很大時,趨向于 1,很小時趨向于 0,因此,該模型的損失函數可以定義如下:
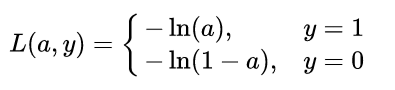
不難發現,由于是分類問題,真實值只有取 0 或 1 兩種情況,當真實值為 1 時,輸出值a越接近 1,則 loss 越小;當真實值為 0 時,輸出值越接近于 0,則 損失函數越小 (可自己手畫一下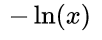 函數的曲線)。因此,可將該分段函數整合為如下函數:
函數的曲線)。因此,可將該分段函數整合為如下函數:
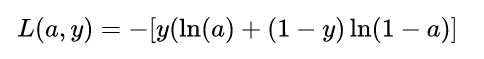
該函數與上述分段函數等價。如果你了解Logistic Regression 模型的基本原理,那么損失函數這一部分與其完全是一致的,現在,我們已經確定了模型的損失函數關于輸出量a的函數形式,接下來的問題自然就是:如何根據該損失函數來優化模型的參數。
3.2 基于梯度下降的逆向傳播過程 (關于損失函數的逆向求導)
這里需要一些先修知識,主要是需要懂得梯度下降 (gradient descent)這一優化算法的原理,這里我就不展開闡述該方法,不了解的讀者可以查看我之前的這篇較為簡單清晰的關于梯度下降法介紹的文章 ->[link]。由于如果將神經網絡的損失函數完全展開將會極為繁瑣,這里我們先根據上面得到的關于輸出量a的損失函數來進行一步步的推導。
BP 的核心點在于逆向傳播,本質上來說,其實是將模型最終的損失函數進行逆向求導的過程,首先,我們需要從輸出層向隱含層的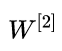 進行求導,也就是需要求得
進行求導,也就是需要求得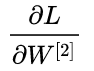 ,這里就需要用到求導方法里的?鏈式求導法則。我們先求得 2 個必要的導數
,這里就需要用到求導方法里的?鏈式求導法則。我們先求得 2 個必要的導數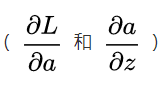 :
:



-
神經網絡
+關注
關注
42文章
4797瀏覽量
102373 -
機器學習
+關注
關注
66文章
8481瀏覽量
133868 -
BP算法
+關注
關注
0文章
8瀏覽量
7227
原文標題:BP 神經網絡 —— 逆向傳播的藝術
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦





 BP神經網絡概述
BP神經網絡概述










評論