圖像處理中濾波和卷積是常用到的操作。兩者在原理上相似，但是在實現的細節上存在一些區別。本篇主要敘述這兩者之間的區別。

濾波

簡單來說，濾波操作就是圖像對應像素與掩膜（mask）的乘積之和。比如有一張圖片和一個掩膜，如下圖：

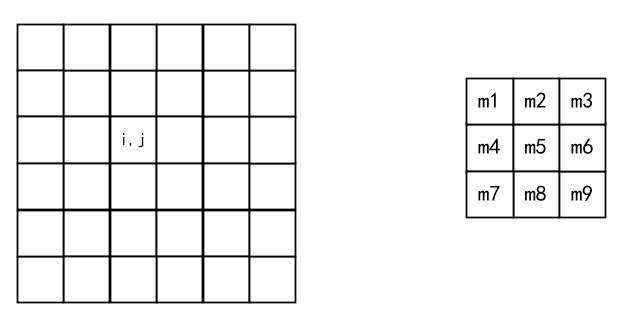
那么像素( i , j )的濾波后結果可以根據以下公式計算：

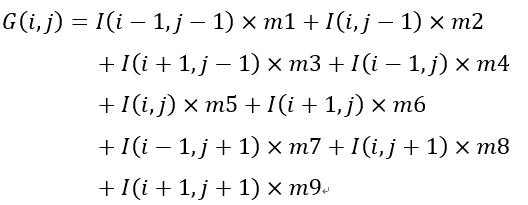
其中G ( i , j )是圖片中 ( i , j )位置像素經過濾波后的像素值。

當掩膜中心m5位置移動到圖像( i , j )像素位置時，圖像( i , j )位置像素稱為錨點。

濾波步驟：

對原始圖像的邊緣進行某種方式的填充（一般為0填充）。

將掩膜劃過整幅圖像，計算圖像中每個像素點的濾波結果。

依照這個步驟，假設我們有一個二維矩陣I，掩膜M，則濾波的結果如下：

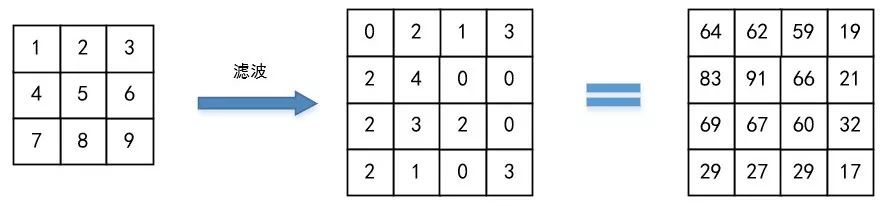
濾波后的圖像大小不變。

卷積

卷積的原理與濾波類似，但是卷積卻有著細小的差別。

卷積操作也是卷積核與圖像對應位置的乘積和。但是卷積操作在做乘積之前，需要先將卷積核翻轉180度，之后再做乘積。

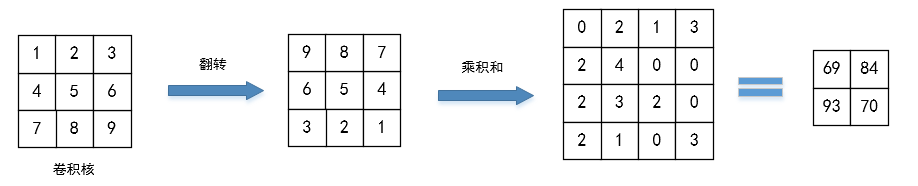
卷積步驟：

180度翻轉卷積核。

不做邊界填充，直接對圖像進行相應位置乘積和。

從以上步驟可以看出，如果卷積核不是中心對稱的，那么卷積和濾波操作將會得到完全不一樣的結果。另外，卷積操作會改變圖像大小！

由于卷積操作會導致圖像變小（損失圖像邊緣），所以為了保證卷積后圖像大小與原圖一致，經常的一種做法是人為的在卷積操作之前對圖像邊緣進行填充。

最后，關于卷積后圖像尺寸的計算：假設原始圖像為 M * M，卷積核大小為 N * N，邊緣填充像素個數為pad，步長為stride。則卷積后圖像的尺寸變為：m = ( M - N + 2 * pad ) / sride + 1。