引 言

微小衛星促進了專用集成電路（ASIC—Application Spceific Integrated Circuit）在航天領域的應用。現場可編程門陣列（FPGA —Field Programable Gate Array）作為ASIC的特殊實現形式，是中國航天目前集成設計的最佳技術選擇，也是中國微小衛星發展的必由之路。

微小衛星對其功耗、質量和體積提出了較苛刻的要求，因此采用FPGA片內冗余容錯代替片外冗余容錯，是實現系統可靠性指標的另一種好辦法。

應用于空間環境的FPGA，其時序邏輯需要防范空間粒子輻射引起的單粒子翻轉，片內三模冗余（TMR） 是應對單粒子翻轉的主要手段。因此，采用FPGA片內冗余容錯方式提高可靠性，是非常必要的。

和其它集成電路一樣，FPGA內部存在制造缺陷。研究發現這些缺陷的空間分布是不均勻的，表現出成團性。FPGA內部缺陷成團對FPGA片內冗余容錯設計會產生負面影響，需要開展針對性的研究并提出應對策略，以提高FPGA片內冗余容錯設計的有效性。

缺陷成團的相關研究

缺陷成團在電子系統設計領域還未被充分認識和重視，但作為集成電路制造領域的研究課題，卻有相當長的研究歷史。

（1） 集成電路缺陷類型

FPGA等集成電路（IC—Integrate Circuit）在制造過程中會產生缺陷。制造缺陷分成全局缺陷和局部缺陷。全局缺陷可以控制，但局部缺陷呈現隨機性，難以避免，并隨著芯片面積的增大而增加。在出廠測試中可以檢測出絕大部分的局部缺陷，但有一些局部缺陷由于其影響一時未能顯現而通過了檢測設備的檢測，這些局部缺陷經過一段時間的使用后會逐步擴展，引起電路故障。空間飛行器選用的FPGA，盡管經過了嚴格的考核和篩選，但由于其工作于惡劣的太空環境，仍然會誘發潛在的微小缺陷，引起電路故障，從而對航天電子產品的可靠性構成嚴重威脅。

（2） 集成電路缺陷的空間分布及成品率預計模型

局部缺陷降低了IC的成品率（Manufacturing Yield），為此需要在成品率預計的基礎上采用相應的冗余容錯措施，以滿足生產成品率要求。

IC芯片（Chip）制作在一定尺寸的硅圓片（Wafer）上，若干個IC芯片在Wafer上按行、列整齊排列，每個芯片內部含有若干個邏輯塊（Logic Block）。FPGA、CPLD、存儲器等IC芯片，其構造邏輯塊在內部也是按行、列整齊排列的。圖1（a）是硅圓片示意圖，內部整齊排列著芯片；圖1（b）是FPGA芯片的示意圖，內部排列著邏輯塊，邏輯塊之間是布線通道。

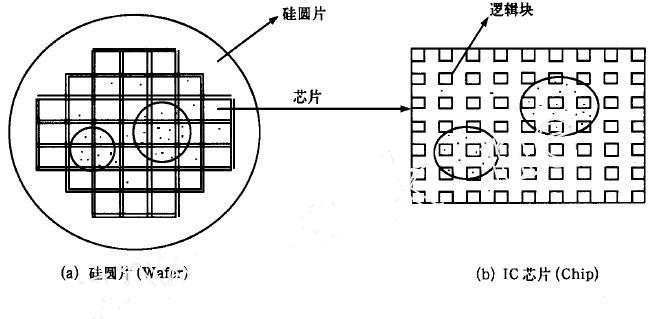
圖1 硅圓片、芯片及內部缺陷分布示意圖

早期研究認為，在Wafer和IC內缺陷的空間分布是均勻的。假定一個IC芯片內部含有n個邏輯塊，每個邏輯塊的平均可靠度為p。對于內部無冗余容錯的IC，成品IC必須是n個邏輯塊均無故障。設P為其預計成品率，則成品率預計模型為

在IC中有規律地增加一些備用邏輯塊，用這些備用邏輯塊代替故障邏輯塊，以提高IC成品率。假定IC有n個邏輯塊，其中r =n - k ，為備用邏輯塊，IC是成品的條件是n個邏輯塊中有k個以上無故障，其概率為

因此采用冗余容錯電路IC的成品率預計模型為

式（2）是IC成品率預計的二項式分布模型。用此模型預計IC成品率，預計值與實際值存在較大差異。大量實驗觀測發現，二項式分布成品率預計模型不準確的根源在于IC內部缺陷的空間分布是不均勻的，呈現成團效應（Clustering）。缺陷成團的主要原因是IC工藝的批次性，工藝條件會隨著時間和空間發生變化，導致IC芯片的批次之間，同一批的圓片與圓片之間，甚至是同一圓片的芯片與芯片之間，缺陷的分布都不同。邏輯塊的可靠度p不是常數，而是隨機變量。

缺陷成團的表象如圖1 所示，圖中黑點代表缺陷，圓框標注的是一個缺陷團。缺陷團面積是個隨機值，大面積缺陷團可以覆蓋整個圓晶片，小面積缺陷團局限在一個芯片內，覆蓋相鄰的若干邏輯塊。

缺陷成團使得鄰近邏輯塊的缺陷存在相關性。要建立反映缺陷成團性的成品率預計模型，需要對復雜的多變量聯合概率密度函數積分，可見用解析方法求得成品率幾乎是不可能的。因此，通常采用數學逼近的方法，依靠系列可解析函數逼近成品率預計模型。

成品率預計的負二項式分布模型和復合泊松（Poisson） 分布模型，如Neymann TypeA ，Poisson Binomial 分布模型，由于考慮了缺陷的成團性，都能較準確地預計成品率。Stapper等假定p服從B分布，提出成品率復合二項式分布模型，這一模型不僅可以較準確地預計IC成品率，而且便于分析計算。成品率復合二項式分布模型為

式中p-是p的均值，u是B分布的一個參數。

式（3）與式（2）相比，是在式（2）的基礎上增加了一個含參數u、p-的比例因子，從而反映出缺陷成團對成品率的影響。

缺陷成團對FPGA片內冗余容錯電路可靠性的影響

衛星電子系統的功能電路布局于FPGA內，功能電路由芯片內的若干簡單邏輯塊構成。為提高功能電路的可靠性，往往需要在片內對功能電路整體采取冗余容錯措施，如最常用的單備份冗余容錯形式。冗余容錯電路包括主份電路、若干備份電路和切換電路，其可靠性是由主份電路、備份電路和切換電路共同決定的。如果主份和備份電路遠比切換電路復雜，則可以忽略切換電路對冗余容錯電路可靠性的影響，以下的討論就是針對這一情況進行的。

對于冗余容錯電路，不允許主份和備份電路都出現故障，引起冗余容錯電路失效。因此有必要采取措施，盡可能降低冗余容錯電路的失效率。

無論是FPGA內邏輯單元一類的簡單邏輯塊，還是處理器陣列中的處理器單元（PE）一類的復雜邏輯塊，都可以采用成品率復合二項式分布模型分析其成品率。若把冗余容錯電路的主份和備份電路分別看成是片內的一個復雜邏輯塊，則可以用此模型分析缺陷成團對冗余容錯電路可靠性產生的影響。

復合二項式分布模型的數學推導

經分析，式（3）給出的成品率復合二項式分布模型表達式存在錯誤，Stapper在文獻中沒有給出推導過程，因此首先從數學上對此模型進行了嚴格推導。推導的關鍵是利用Γ函數與B函數的關系：

缺陷成團對冗余容錯電路可靠性影響分析

式（4）中的第三項對應n冗余容錯電路的無故障概率Pn為

式（4） 中的第一項對應n 冗余容錯電路的失效率Qn 為

分析式（5） 、（6） ，當參數u 趨近于無窮大時

當參數u 趨近于零時

式（7）、（8）表明，當參數u 趨近于無窮大時，Pn和Qn的值等于缺陷均勻分布時的值，說明此時缺陷不具備成團性，而是呈均勻分布狀態； 式（9）、（10）表明，當參數u趨近于零時，Pn和Qn的值分別等于主份電路的可靠度和共效率。

參數u反映了IC 內部缺陷成團性的強弱，稱為模型的成團因子。u 越大，缺陷成團性越弱；u 越小，缺陷成團性越強。

進一步分析表達式（5）、（6），對于任意的u》0 ，由于

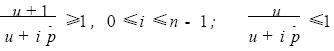
缺陷成團時片內冗余容錯電路的無故障概率和失效率比缺陷均勻分布時的都要高。缺陷成團性增大了冗余容錯電路的失效率，削弱了冗余容錯的可靠性增長功效。

其值隨參數u增大而增大，因此失效率Qn隨參數u增大而減小，并且在u=0時取得最大值。成團因子u越大，冗余容錯電路的失效率越低、可靠性就越高。這一結論對冗余容錯電路可靠性設計具有重要指導意義。

成團因子

缺陷成團性強弱可以理解為缺陷相關性的強弱。缺陷成團性越強，缺陷相關性就越強，成團因子越小，反之亦然。若應用式（4）分析一個冗余容錯電路，則成團因子反映的是冗余容錯電。路內缺陷的平均相關度缺陷團面積是個隨機值，當冗余容錯電路面積小于最小缺陷團面積時，相應成團因子的值只取決于缺陷團內缺陷相關性的強弱，與冗余容錯電路面積無關；當冗余容錯電路面積大于最大缺陷團面積時，此時成團因子不僅受缺陷成團性強弱的影響，而且隨冗余容錯電路面積的變化而變化。

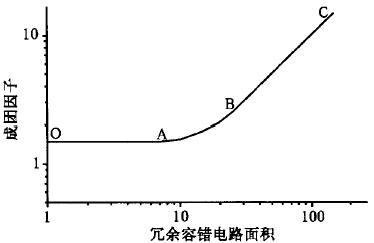
圖2 成團因子α與冗余容錯電路面積的關系

IC成品率預計常用到負二項式分布模型，此模型中的參數α是模型的成團因子。Stapper采用回歸分析法分析驗證成團因子α，得出成團因子與冗余容錯電路面積的關系，如圖2所示。曲線中的OA水平直線段表示α維持不變，對應冗余容錯電路面積小于所有缺陷團面積的情況；曲線中的BC直線段表明α與冗余容錯電路塊面積成正比，對應冗余容錯電路面積大于所有缺陷團面積的情況； 曲線中的AB曲線段表明α隨冗余容錯電路面積增大而呈現非線性增長，此時冗余容錯電路面積介于最小缺陷團面積和最大缺陷團面積之間。

在沒有缺陷團面積數據時，一般假定FPGA內缺陷團面積小至邏輯塊，大至整個芯片，并且在這范圍內連續分布。此時圖2中的點A、B分別趨近點O、C，在曲線整個范圍內，成團因子隨冗余容錯電路塊面積增大而呈非線性增長。

實驗數據表明，在冗余容錯電路面積小于所有缺陷團面積時，成團成子u維持不變。成團因子α和u物理意義相同，遵循相似的變化規律。

缺陷成團時提高冗余容錯電路可靠性的策略

冗余容錯電路的主份和備份電路布局于FPGA芯片內。當FPGA內缺陷成團時，可以通過調整布局，增大主、備份電路的幾何距離，降低冗余容錯電路的失效率。

分析表明，在缺陷成團時，冗余容錯電路的失效率取決于所對應成團因子的大小。成團因子決定于冗余容錯電路的等效面積。冗余容錯電路的等效面積等于涵蓋整個冗余容錯電路的最小面積，如圖3所示。增大主、備份電路的幾何距率，就是增大冗余容錯電路的等效面積，從而增大對應成團因子的值。增大成團因子，就能降低冗余容錯電路的失效率，提高其可靠性。

圖3 冗余容錯電路布局示意圖

提高冗余容錯電路可靠性策略的定量分析

由于成團因子與冗余容錯電路等效面積之間存在復雜非線性關系，無法為上述策略建立分析模型進行定量分析。但當FPGA內只有小于冗余容錯電路面積的缺陷團，且成團因子與冗余容錯電路等效面積成線性關系，或者可以用線性關系近似時，則可以建立相應的分析模型進行定量分析。

考慮一個單模塊單備份容錯電路，如圖3 所示。A 是主份電路，B 是備份電路。如果單純考慮信號時延，則布局時應將主、備份電路相鄰排列。稱這一布局為單模塊單備份容錯電路的基本布局，基本布局的等效面積為2S0（S0為主份電路面積） ，此時主、備份電路之間的距離為0，對應成團因子為u0，則有基本布局的失效概率Q02為

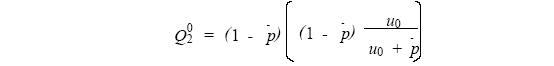
增大主、備份電路的距離，在主、備份之間留有面積等于m 個主份電路面積的空間。此布局為調整布局。調整布局的等效面積為（m+2）S0 ，此時主、備份電路之間的距離為m ，對應成團因子為um 。

um 和u0有如下關系

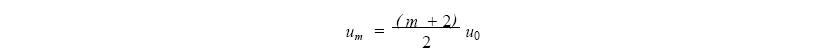
調整布局的失效率Qm

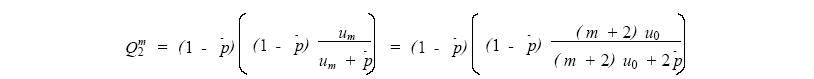
無論成團因子u0取何值，調整布局都能夠降低冗余容錯電路的失效率。表1 數據反映的是基本布局和特定調整布局（m=2）失效率隨成團因子u0的變化情況，主份電路的可靠度p-=0.99999。

在成團因子較寬的一個變化范圍內，特定調整布局（m=2）失效率比基本布局失效率降低了約1/2。

表1 失效率隨成團因子u0 變化表

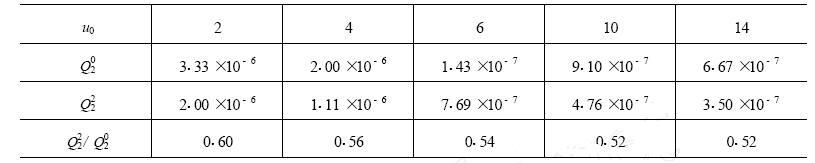
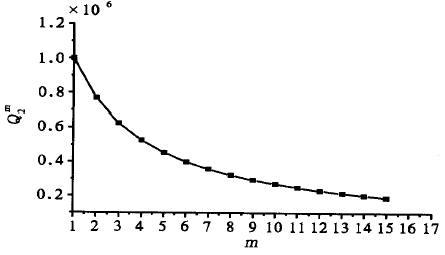
圖4 冗余容錯電路失效率隨距離變化關系

冗余容錯電路的主、備份電路間距離越大，冗余容錯電路失效率越低。圖4是冗余容錯電路失效率隨主、備份電路之間的距離變化（m變化）的情況，曲線對應的主份電路可靠度p-= 0.99999，成團因子u0=6。

表2 列出了不同布局失效率的具體改善數據，當m=8時，失效率約為基本布局的1/5。

表2 冗余容錯電路失效率隨布局變化表

缺陷成團時芯片內備份電路的優化布局原則

每種冗余容錯方式，在FPGA的矩形（含正方形） 芯片內實現時，可以選擇不同的布局方案。應用本章提出的策略，針對常用的幾種冗余容錯方式，從可靠性角度提出了最佳的一個布局方案。

圖5（a）是單模塊單備份容錯形式。按圖5（b）所示，將主、備份電路沿芯片對角線布置，可以獲得最低的失效率。切換電路布置在與主、備份電路距離相同的位置上，保證切換電路的兩路輸入信號時延基本相同。主、備份電路的輸入分別從就近的芯片引腳輸入，避免占用內部大量的互連資源。兩引腳再通過PCB板上的印制線相連。

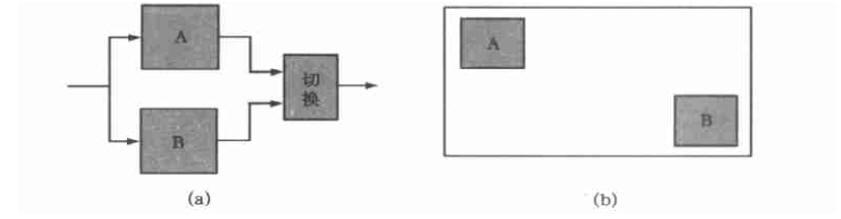
圖5 單模塊單備份容錯形式布局

布局、時延與資源利用率

依據本章提出的策略進行布局，冗余容錯模塊之間存在較大的空間，在這空間里可以布置其他功能電路。但是冗余容錯模塊之間的長距離信號連接需要消耗FPGA內有限的連線資源，往往由于連線資源消耗殆盡，無法繼續布置其他的功能電路，從而降低了芯片邏輯資源的利用率。因此，冗余容錯模塊可靠性的提升也是以犧牲資源為代價的。解決這一問題的一個有效辦法是利用FPGA豐富的輸入輸出管腳資源，將片內的長線連接改為片外PCB板印制導線的連接。

無論是片內的還是片外的長線連接，都勢必引起較大的信號時延，這會限制電路的最高工作頻率，但隨著FPGA性能的不斷改善，信號時延問題會逐步緩解。

結束語

基本FPGA的片內冗余容錯將會是提高微小衛星可靠性的重要手段。隨著FPGA規模的增大和集成密度的提高，內部缺陷發生的概率也在增大，因此研究缺陷成團性對片內冗余容錯的影響，具有較重要的工程價值。后續工作需要研究缺陷成團對一些常用片內冗余容錯方式如TMR的影響，提出相應的應對策略。在此基礎上再進一步探討在電子設計自動化環境下，高效實現應對缺陷成團性策略的方法。