據報道，近日，斯坦福大學的工程師們在加州著名的雷山賽道公園完成了經改良的奧迪 TTS 無人駕駛，圈速甚至超過了有人駕駛車輛。這輛改良過的賽車奧迪 TTS 名為「雪萊」。斯坦福大學的教授已經從事無人車輛的線控底盤控制許多年了，希望能夠實現無人駕駛的高速行駛以及提高無人駕駛的安全性。

對輪胎附著能力的利用程度對緊急工況或者競速中的車輛而言是至關重要的，當轉向不足車輛在極限過彎的時候發生前軸飽和，轉向系統已經失去了路徑跟蹤的能力。無人駕駛車輛的試驗數據表明，在附著極限下通過轉向操作進行路徑跟蹤，要求附著系數的誤差在大約 2% 以內。這完全超過了現有的實時路面附著系數估計算法的能力。收集的專業賽車駕駛員的駕駛數據，得出新穎的控制框架，基于側偏角的控制策略——保持前輪處于最大輪胎附著利用率的側偏角，以及相應路徑跟蹤的縱向車速控制方法。這個方法最大的好處是大大降低了對于附著系數估計精度的依賴。本研究基于這一概念設計了控制器，試驗結果表明在附著系數未知的前提下，車輛在附著極限下也能夠成功跟蹤圓周路徑。

1 前言

擴大車輛的行駛極限需要盡可能地利用輪胎的附著能力。相應地，這也能夠提高車輛避障的能力、防止車輛偏離道路、降低碰撞的損傷，甚至提高車輛比賽的圈速成績。隨著線控底盤技術的發展，即使在輪胎附著極限的情況下，ADAS 和智能駕駛系統也有可能通過連續的控制來提高車輛的安全性。

Kritayakirana 為路徑跟蹤而設計的速度跟蹤和獨立轉向控制系統證明了智能汽車在附著極限下的控制可行性[1]。Beal 和 Gerdes 利用 MPC 算法設計了智能車輛在極限工況下的側向動力學控制系統[2]。這兩套控制系統都要求對路面附著系數進行估計，并且在試驗中都運用了離線的估計結果。而實際使用過程中需要將附著系數替換成在線的估計結果。

Hsu 在單純轉向工況中利用轉向力矩來試試估計路面附著系數[3]。Hahn 同樣利用車輛側向動力學設計了車輛參數實時辨識算法來估計路面附著系數和輪胎的側偏剛度[4]。Ray 利用側向和縱向動力學設計了一個基于貝葉斯假設的測試框架，從統計數據上看，觀測器能夠很好地估計不同的附著程度假設的輪胎力[5]- [9]。

在極限行駛工況下，轉向控制已經不是路徑跟蹤的有效控制輸入了，因為此時再增大轉角也已經無法增加行駛的曲率——曲率的上限取決于車速。因此，極限工況下路徑跟蹤的典型轉角控制需要準確估計給定曲率和地形的路徑下允許的最大車速。這意味著需要準確估計路面的附著系數。本文中試驗數據表明這樣的控制器需要路面附著系數的估計誤差在大約 2% 以內才能達到與專業賽車駕駛員在極限行駛過程中同等的行駛性能。而這要求超出了現有的實時估計算法的能力范疇。

在緊接著的賽道測試中，一名專業駕駛員表明，他的圈速比智能駕駛控制系統的更快，主要是因為他能夠更好地利用輪胎附著能力。記錄的數據催生出一個針對不足轉向車輛轉向過程的基于輪胎側偏角的轉角控制方法，目的是讓前輪保持在最大輪胎力對應的側偏角上。另外，相比于轉角控制，大家公認的是速度反饋也能夠用于路徑跟蹤。這會是一個全新的控制架構，能夠讓智能汽車在跟蹤目標路徑的同時盡可能地利用輪胎的附著能力。對輪胎模型的分析可知，對路面附著系數的實時估計精度要求遠低于利用轉角控制實現路徑跟蹤的估計精度要求。

為了驗證這一控制邏輯，一個新的縱向速度控制器被設計出來跟蹤一個圓周路徑，另外由 Subosits 和 Gerdes 設計的一個基于車輪側偏角的轉向控制器被用來控制前輪在給定滑移率下保持最大輪胎力對應的側偏角[10]。縱向速度控制器和側偏角控制器都需要估計路面附著系數，因此根據 Ray 的假設測試算法建立了基于側向動力學路面附著系數的在線估計器[5]- [9]。

第二部分介紹了該研究用到的車輛和車輛建模。而在第三部分，賽道的收集數據表明，對于一個基于轉角控制的智能駕駛路徑跟蹤器，路面附著系數的估計誤差要求在大約 2% 以內。同時，專業賽車駕駛員的行駛數據中迸發出一個新的方法來更有效利用車輪的附著能力。第四部分介紹了一個類似的智能駕駛控制器。第五部分的試驗結果表明在附著情況未知的情況下，本文提出的控制架構和在線附著估計器能夠在極限工況下成功地跟蹤給定的圓周路徑。

圖 1無人駕駛 Audi TTS Quattro 研究車輛

圖 2平面車輛單軌模型和路徑跟蹤狀態

2 試驗車輛與車輛模型

A．試驗車輛介紹

一輛 2009 年 Audi TTS Quattro 試驗車輛，如圖1 所示，裝備了一個主動液壓主缸、DSG 變速箱、EPS、電子節氣門和整車 CAN 網絡。無人駕駛控制器運行以 200Hz 的頻率運行中 dSPACE 公司的 MicroAutoBoxII 上面，一臺 OxTS RT4003 慣性導航儀和差分 GPS 被安裝在測試車輛上，用于測量車輛和路徑跟蹤的狀態。轉角控制器由 Kapania 和 Gerdes 設計完成[11]。本文的數據是在美國加州威洛斯的雷山賽道公園采集的。

B．車輛動力學建模

一個平面單軌車輛模型，如圖2 所示，為數據分析和控制器設計提供了一個簡單而直觀的車輛模型。在這個模型中，同一軸上的兩個車輪被近似為一個集中車輪，從而模擬穩態的側向載荷轉移等影響因素。該模型有三個速度狀態：縱向速度 Ux、側向速度 Uy 和橫擺角速度 r。除了車輛的速度狀態外，圖2 還描繪了車輛質心出的合速度 V、質心側偏角 β 和轉向角 δ。另外，為了表示車輛和路徑的關系，沿著路徑的距離 s 和側向位移誤差 e 也被標出。車輛航向 ψ 和路徑的航向 ψr 之間的偏差用來 △ψ 表示。

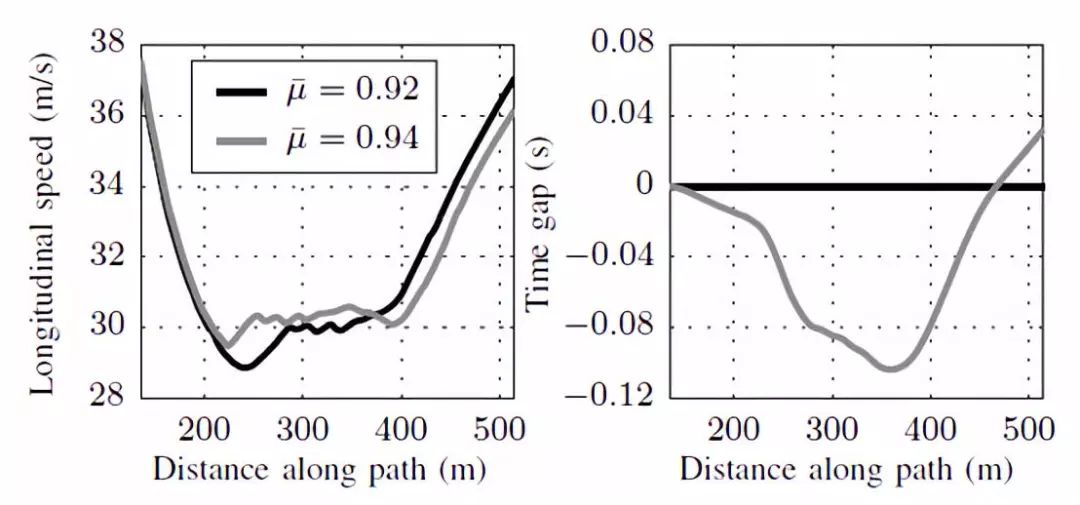
圖 3第 2 道彎中測量的速度數據（左）

和相應的時間差距（右）

（跟蹤分別由 μ=0.92 和 0.94 生成的不同速度配置）

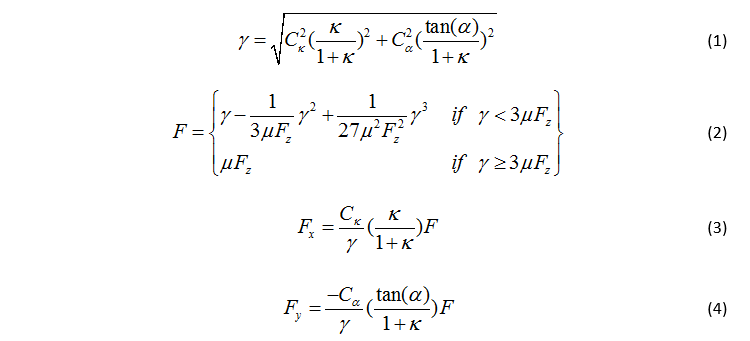
C．輪胎模型

每個車軸上的等效集中車輪力是用單一附著系數的刷子輪胎模型來建模[12]，例子可以參考 Hindiyeh 的論文[13]。在這一模型中，等效輪胎可以通過側向剛度 Cα 和縱向剛度 Cκ 來表征，兩個參數可以通過直線制動和斜坡轉角輸入來辨識得到，后者在 Voser 的論文[14]中有介紹。縱向力 Fx 和側向力 Fy，如圖2 所示，是側偏角 α、滑移率 κ、垂直載荷 Fz 以及路面附著系數μ的函數。當 γ≥3μFz 的時候，輪胎出現飽和，并且有最大輪胎力。在單純轉向操作過程中，沒有驅動力矩或者制動力作用在車輪上，κ=0，對應最大側向力的峰值側偏角 αpeak 為：

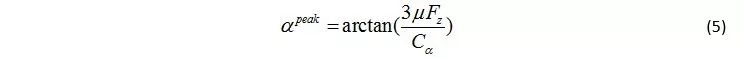
3 極限行駛

圖3 是無人駕駛車輛在經過第二個彎道（一個較長的左轉彎）的縱向車速。參考路徑是基于回旋曲線非線性優化得到的[15]。而這二維的路徑對應的速度分布圖是綜合考慮三維地形因素得到的[16]。分別跟蹤的兩個不同的速度分布圖如圖3：其中一個要求路面附著系數大于 0.92，另外一個稍微快一點的則要求附著系數大于 0.94。這兩組估計值是通過經驗值選取的，并且是為了最小圈速而選擇的。

A．無人駕駛車輛路徑跟蹤的速度跟蹤和獨立轉向控制

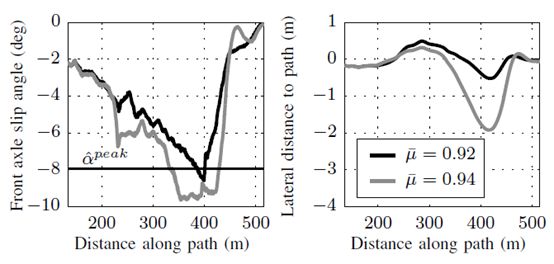
圖 4第 2 道彎中測量的前軸側偏角（左）

和側向位移誤差（右）

（跟蹤分別由 μ=0.92 和 0.94 生成的不同速度配置）

另外圖3 還指出了沿著參考路徑行駛時以更快的速度分布圖為目標的車輛相對另一輛的時間差距。不同的車輛行駛距離和速度下，相對的時間差距都在變化，這與輪胎利用程度有關。

跟蹤較快的速度圖的車輛以稍微快一點的車速入彎。而且在彎中的車速也是附著系數估計值更大的車輛更高，負的相對時間差距表明，在彎道的前部分，跟蹤較大附著系數估計值對應速度圖的車輛耗時更少。但是，在出彎之前，車輛的速度開始降低，出口處的車速甚至比跟蹤低附著系數估計值對應速度圖的車輛更低。盡管該車在彎中以前領先了 0.1s，但是最終它完成整個轉彎工況耗費了更多的 0.03s。

伴隨著更高的速度分布圖，初始的車輛側偏角更大，如所示。相對地，低附著系數估計值的車輛的前軸側偏角則緩慢地增加至 -8 度。聯邦 595EVO 輪胎的斜坡轉角輸入測試數據表明該款輪胎的峰值側偏角大約是 7.9 度。在彎道的后半段，車輛跟蹤較高附著系數估計值對應的速度圖時的側偏角超過了峰值點，因此前輪輪胎力飽和了。由于側向力發生飽和，車輛的縱向控制器將驅動力矩降低到零，再加上前軸側向力矢量的額外旋轉帶來的阻力，車輛的速度降低的更多。前軸在這樣的車速下不能產生足夠的側向力來維持車輛行駛在參考路徑上，在圖4 可見，由于車輛滑向彎道外側，側向位移誤差也逐漸增大。

當車輛以更高的車速行駛的同時還能跟蹤上目標路徑，這意味著 μ=0.94 對應的車輛在彎道的前半部分能夠更好地利用輪胎的附著力。但是在彎道的后半部分，該車不再能夠跟蹤上目標的路徑，最后花了更多的時間來完成整個彎道。在這里，附著系數估計值為 μ=0.92 的車輛能夠更有效地利用輪胎附著力。這一結果以及更多的測試都表明，現有的控制系統要求附著系數的估計誤差在大約 2% 以內才能滿足路徑跟蹤的要求。

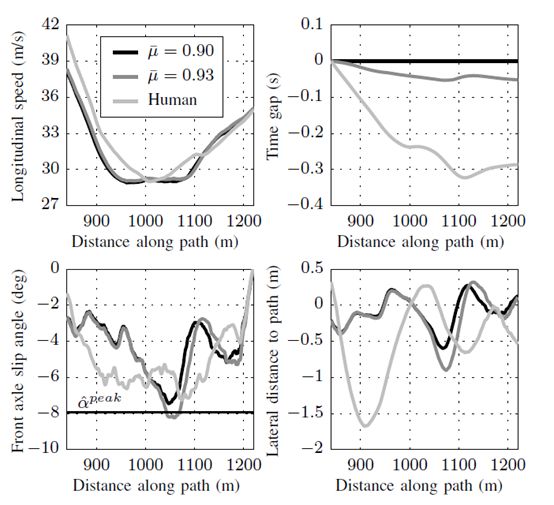
圖 5專業駕駛員在第二道彎相比于跟蹤 μ=0.90 和 μ=0.93 的速度分布圖的無人駕駛車輛的各項性能表現

B．有人駕駛 VS.無人駕駛

圖5 對比了無人駕駛在跟蹤參考路徑時和專業賽車駕駛員的縱向車速、時間差、前軸側偏角和側向位移誤差。這條路徑時通過凸函數優化方法生成的，與 Kapania 的方法類似[17]。圖中三條曲線分別是無人駕駛車輛跟蹤 μ=0.90 和 μ=0.93 的速度分布圖時的數據以及駕駛員十圈內最好的成績。

開始階段，由于明顯更高的入彎速度，賽車駕駛員相比無人駕駛模式領先了 0.24s。他沿著較寬的入彎路線行駛，然后迅速獲得了大約 -6 度的前軸側偏角，并且在整個彎道都保持在這個值附近。他的最高車速和無人駕駛模型下的車輛很接近，但不同的是，他在駛出彎道前迅速提高了車速。當無人駕駛模式的車輛以 μ=0.93 的速度分布圖行駛時，車輪在彎道中間達到飽和，大概是 1000m 的位置，從而車輛失去了路徑跟蹤的能力，因此損失了大約 0.02s。

相反，專業駕駛員在彎道很早的部分就前軸獲得了大約 -6 度的側偏角。這意味著車輛在制動之后能夠迅速獲得較大的側向力。而無人駕駛的車輛在前軸處產生的側偏角使得車輛獲得較小的側向力，因此輪胎的附著力并沒有得到完全利用。通過將側偏角維持在 -6 度左右，駕駛員能夠在整個彎道中都有效地利用輪胎的附著能力，使得他相比無人駕駛的車輛能夠以更少的時間完成整個彎道。

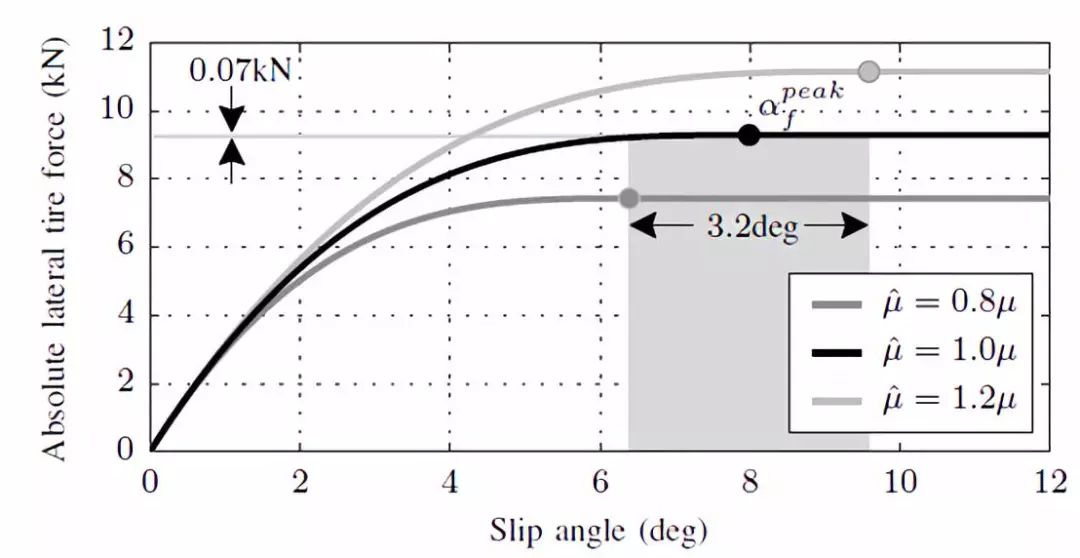
圖 6不同附著系數下側向力和輪胎側偏角的關系，以及由（4）計算得到的峰值側偏角對聯邦 EVO595 輪胎而言，Cαf=200kN/rad，μf=0.97，κf=0

4 極限工況下的路徑跟蹤

A．極限工況下的側偏角控制方法

圖6 分別指出在不考慮縱向滑移率以及路面附著系數估計值等于實際值或相差 20% 的條件下，側向力和輪胎側偏角之間的關系曲線。同時還標出了相應的峰值側偏角。

通過在線估計路面附著系數和公式(5)，可以計算得到峰值側偏角作為轉角控制的目標以實現輪胎附著能力的最大化利用。考慮實際路面估計精度的限值，當路面附著系數高估了 20% 的時候，由于輪胎曲線的特性，即使輪胎處于較大的側偏角下依然能夠產生最大的側向力。當附著系數低估 20% 的時候，輪胎側偏角的峰值點被低估了約 1.6 度，可是此時的輪胎力僅僅下降了 0.8%。

圖6 表明，在一個相對較大范圍內的側偏角，輪胎的側向力都比較接近峰值點。因此，在極限工況下，基于輪胎側偏角設計的控制器比一般基于精確的最大速度限值的控制系統對路面附著系數的估計精度要求更低，而且性能要求也比較合適。

B．在線估計路面附著系數

Ray[5]-[9]指出，貝葉斯假設測試算法能夠在車輛的操縱極限工況下提供一個實時的路面附著系數估計結果。事實證明，由于前后軸輪胎力產生的橫擺力矩以及試驗車輛上安裝了不可控的主動制動力分配系統（EBD），不能準確地獲取輪胎力。然而，通過引入拓展卡爾曼濾波的估計器，通過測量車輛的速度、加速度、姿態角和角速度，能夠很好地估計出作用在車輛上的外力和外力矩。

接下來，在估計器的第二部分引入了車輛的單軌模型假設。通過估計的合力以及單軌模型中前后軸輪胎力的靜態關系，即使在不完全平整的路面上也能夠得到滿足穩態轉向工況下附著系數估計要求的輪胎力。前后軸的路面附著情況假設一致，并且通過估計的側向力和合力最終得到附著系數的估計結果。

C．轉角控制器設計

本文主要研究極限工況下的不足轉向車輛，因此，設計的轉角控制器主要是控制前軸的輪胎力。最大的輪胎力對應的輪胎側偏角可以通過公式(2)計算得到：

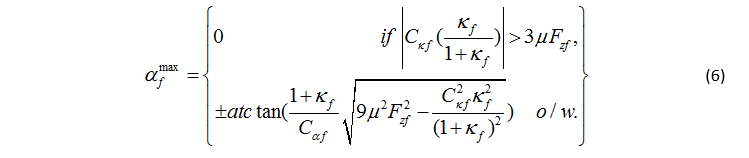
前軸的等效縱向滑移率是通過對左右側車輪的滑移率加權得到的，在側向加速度增加到 7m/s2 時，由于側向載荷轉移的關系，外側車輪的權重接近 80%。通過測量的縱向滑移率和實時路面附著系數估計結果可以計算得到前軸的最大側偏角。而這個側偏角就直接作為底層轉角控制器的輸入，方向由目標路徑的曲率確定。

D．極限工況下的路徑跟蹤控制

圖2 中平面三自由度的單軌車輛模型的狀態方程如下：

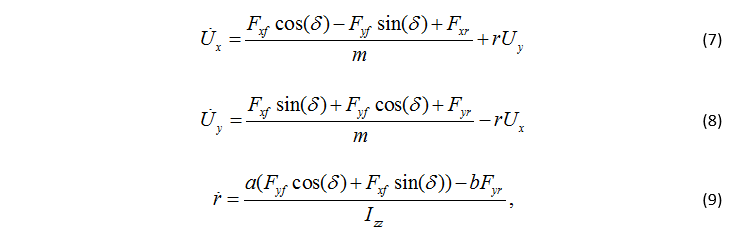
其中，m 和 Izz 分別是車輛的質量和橫擺轉動慣量。a 和 b 分別是質心到前軸和后軸的距離。

在穩態條件下，假設轉角和前軸的縱向力都比較小，公式(8)可以簡化為：

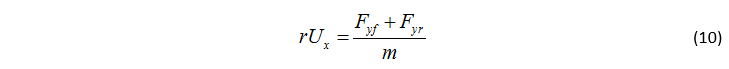
如果前后軸同時處于最大的輪胎力，并且每根軸的附著能力都由單一附著系數來表征，那么橫擺角速度和車速之間的耦合關系可以用式(11)來表示。

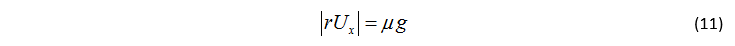
文獻[18]中，Goh 和 Gerdes 針對漂移車輛設計了一個用橫擺角速度作為輸入的路徑跟蹤控制器。而在本文中，類似的控制器可以作為車輛極限工況下的路徑跟蹤控制器，利用縱向速度來控制預瞄點的誤差：

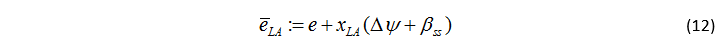
其中，xLA 是預瞄距離。通過引入穩態的質心側偏角，當車輛模型足夠精確時便可以消除預瞄點的誤差，從而使車輛準確跟蹤穩態的轉向。預瞄點的誤差導數為：

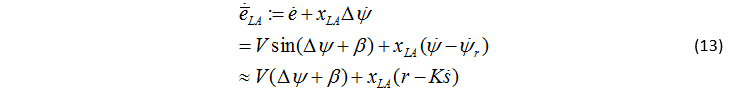
其中，K 是路徑的曲率。假設預瞄點的誤差具有穩態的一階動態，則：

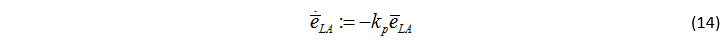
曲率為 K 的路徑在附著極限下的穩態車速大概為：

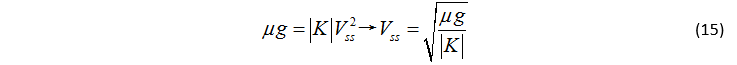
將式(12)和(13)代入(14)，可得，

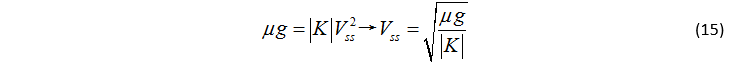
得到橫擺角速度作為虛擬的控制輸入：

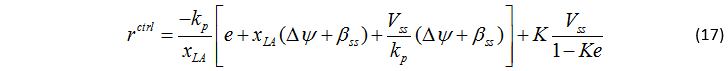
當誤差為零、航向角誤差等于質心側偏角的時候，車輛的控制橫擺角速度便等于參考路徑的航向角速度。最后，通過式(11)可以將橫擺角速度控制輸入轉化為路徑跟蹤控制器的縱向速度控制量：

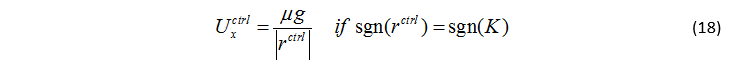
當預瞄點在彎道的內側時，誤差過大會導致目標的橫擺角速度方向和路徑的曲率相反。此時，為了保證車輛加速并跟蹤上參考路徑，目標車速將會過大。

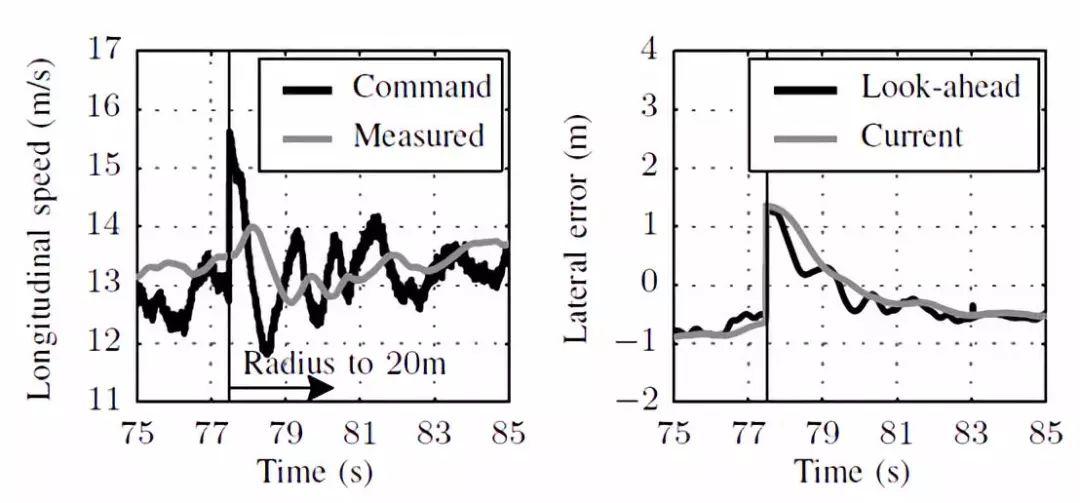
圖 7跟蹤的縱向車速（左）和預瞄點以及實際的側向位移誤差（右）

為了簡化控制算法，采用了比例反饋控制來跟蹤參考的縱向車速，并且為了補償路面的阻力和坡度，采用了前饋控制。

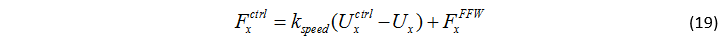
目標的車速控制可以通過發動機的 MAP 圖和電子節氣門來實現。

5 試驗結果

試驗車輛安裝了普利司通的 Potenza S-04 輪胎來測試新的控制系統。斜坡轉角輸入的測試結果表明車輛的前后軸輪胎的等效側偏剛度分別為 220kN/rad 和 240kN/rad，附著系數分別為 0.99 和 1.04。直線制動測試結果表明前后軸的有效縱向剛度為 450kN。控制器中的參數 XLA=10m，kp=1/s，kspeed=1000Ns/m。參考路徑設為一個半徑突變的逆時針圓周，從而驗證車輛的路徑跟蹤性能。試驗場地路面為向西傾斜 2.5 度的干凈柏油路面。

圖 8 分別是路面附著系數的估計結果和輪胎側偏角跟蹤目標值，圓周半徑在 77.5s 的時候從 18m 變為 20m。基于估計的輪胎參數，峰值側偏角為 7.4 度。測量的側偏角比目標值稍大，可能是由于側偏角控制器中轉向力矩的建模存在一定誤差，但是前軸的輪胎力也得到了充分的利用（如圖6 所示）。估計器的路面附著系數估計結果在 1 和 1.1 之間，與轉角斜坡輸入工況下的估計結果一致。

圖 7 是車輛跟蹤路徑時的車速目標值和測量值。較小的 kp 和較大的 kspeed 參數對車速跟蹤控制效果更好。如圖9 所示，側向位移誤差在轉向半徑突變后逐漸收斂，并最終穩定在 1m 左右，車輛在目標軌跡的外側。而這部分偏差還需要更深入的研究。

圖 8路面附著系數估計結果（左）和路徑跟蹤的前軸側偏角的目標值和測量值（右）

圖 9路徑跟蹤結果（俯視）

6 結論

試驗數據表明在路徑跟蹤過程中的速度跟蹤控制和轉角控制需要路面附著系數的估計誤差在大約 2% 以內。然而，基于輪胎側偏角設計的轉角控制能夠有效降低系統對于路面附著系數估計結果精度的依賴。采集到的專業賽車駕駛員數據指出通過側偏角控制能夠使得不足轉向的車輛更充分地利用輪胎的附著能力，并且可以通過速度反饋來實現路徑跟蹤。

為了驗證這一理念，設計了根據虛擬橫擺角速度控制輸入得到的速度控制量來進行路徑跟蹤。貝葉斯濾波在線估計器和試驗數據表明，即使在路面附著系數不確定的條件下，控制器也能夠很好地跟蹤上圓周路徑。

不管是在賽道競速或者公路上的緊急工況，文章設計的控制架構在極限工況下的無人駕駛都能夠有很好地應用前景。未來的研究將進一步考慮縱向車速控制的建模、不同控制系統對附著系數的靈敏度、變曲率的路徑跟蹤、地形和輪胎的影響、以及路面附著系數不一致的情況。

7 參考文獻

[1] K. Kritayakirana, “Autonomous vehiclecontrol at the limits of handling,” Ph.D. dissertation, Stanford University,2012.

[2] C. E. Beal and J. C. Gerdes, “Modelpredictive control for vehicle stabilization at the limits of handling,” IEEETransactions on Control Systems Technology, vol. 21, no. 4, pp. 1258–1269,2013.

[3] Y.-H. J. Hsu, S. M. Laws, and J. C.Gerdes, “Estimation of tire slip angle and friction limits using steeringtorque,” IEEE Transactions on Control Systems Technology, vol. 18, no. 4, pp.896–907, 2010.

[4] J.-O. Hahn, R. Rajamani, and L.Alexander, “GPS-based real-time identification of tire-road frictioncoefficient,” IEEE Transactions on Control Systems Technology, vol. 10, no. 3,pp. 331–343, 2002.

[5] L. R. Ray, “Nonlinear estimation ofvehicle state and tire forces,” in American Control Conference, 1992. IEEE,1992, pp. 526–530.

[6] L. R. Ray, “Real time determination ofroad coefficient of friction for IVHS and advanced vehicle control,” inAmerican Control Conference, Proceedings of the 1995, vol. 3. IEEE, 1995, pp.2133–2137.

[7] L. R. Ray, “Nonlinear state and tireforce estimation for advanced vehicle control,” Control Systems Technology,IEEE Transactions on, vol. 3, no. 1, pp. 117–124, 1995.

[8] L. R. Ray, “Nonlinear tire forceestimation and road friction identification: Simulation and experiments,”Automatica, vol. 33, no. 10, pp. 1819–1833, 1997.

[9] L. R. Ray, “Experimental determinationof tire forces and road friction,” in American Control Conference, 1998.Proceedings of the 1998, vol. 3. IEEE, 1998, pp. 1843–1847.

[10] J. Subosits and J. C. Gerdes, “Asynthetic input approach to slip angle based steering control for autonomousvehicles,” in 2017 American Control Conference (ACC). IEEE, 2017 (in press).

[11] N. R. Kapania and J. C. Gerdes,“Design of a feedback-feedforward steering controller for accurate pathtracking and stability at the limits of handling,” Vehicle System Dynamics,vol. 53, no. 12, pp. 1687– 1704, 2015.

[12] H. Pacejka, Tyre and Vehicle Dynamics,3rd ed. Butterworth- Heinemann, 2012.

[13] R. Y. Hindiyeh, “Dynamics and controlof drifting in automobiles,” Ph.D. dissertation, Stanford University, 2013.

[14] C. Voser, R. Y. Hindiyeh, and J. C.Gerdes, “Analysis and control of high sideslip manoeuvres,” Vehicle SystemDynamics, vol. 48, no. S1, pp. 317–336, 2010.

[15] P. A. Theodosis and J. C. Gerdes,“Nonlinear optimization of a racing line for an autonomous racecar usingprofessional driving techniques,” in ASME 2012 5th Annual Dynamic Systems andControl Conference joint with the JSME 2012 11th Motion and VibrationConference. American Society of Mechanical Engineers, 2012, pp. 235–241.

[16] J. Subosits and J. C. Gerdes,“Autonomous vehicle control for emergency maneuvers: The effect of topography,”in 2015 American Control Conference (ACC). IEEE, 2015, pp. 1405–1410.

[17] N. R. Kapania, J. Subosits, and J. C.Gerdes, “A sequential two-step algorithm for fast generation of vehicle racingtrajectories,” Journal of Dynamic Systems, Measurement, and Control, vol. 138,no. 9, p. 091005, 2016.

[18] J. Y. Goh and J. C. Gerdes,“Simultaneous stabilization and tracking of basic automobile driftingtrajectories,” in 2016 IEEE Intelligent Vehicles Symposium (IV). IEEE, 2016,pp. 597–602.