文字簡(jiǎn)明扼要，語音更加詳細(xì)生動(dòng)哦。

繼續(xù)上一篇，本文對(duì)離散信號(hào)的頻域分析（共5節(jié)）中的第3節(jié)——離散傅里葉變換DFT（Discrete- Fourier Transform）中的第4個(gè)問題：3.4 DFT性質(zhì)中的后兩個(gè)進(jìn)行講解。

3.4 DFT的性質(zhì)

以下四個(gè)性質(zhì)，上一篇中已經(jīng)學(xué)習(xí)了前兩個(gè)，本文對(duì)前后個(gè)性質(zhì)——圓周共軛對(duì)稱性、Parseval定理進(jìn)行講解。

3、圓周共軛對(duì)稱性

這里不講證明（教材上都有），重點(diǎn)講怎么理解教材上讓人眼花繚亂的公式。我們把“公式”翻譯成“人話”。

首先說明一下，本文中所說的N點(diǎn)長序列，都指的是自變量取值范圍為0~N-1，除此之外的區(qū)間，序列值為0。

先看第一個(gè)。

（1）共軛序列的DFT

時(shí)頻域有這樣一個(gè)基本對(duì)應(yīng)關(guān)系——時(shí)域取共軛，對(duì)應(yīng)頻域自變量取負(fù)然后函數(shù)取共軛。具體到DFT呢？“自變量取負(fù)”也就是“反轉(zhuǎn)”，而“DFT隱含著周期性”，所以這里的“反轉(zhuǎn)”要加上“周期延拓，再取主值區(qū)間”，所以，公式及證明過程如下：

圖1

時(shí)域取共軛，對(duì)應(yīng)DFT是：先周期延拓，再反轉(zhuǎn)，再取主值區(qū)間，最后取共軛。當(dāng)然，第一步與第二步可以交換次序，取共軛可以放在任意步驟上。關(guān)鍵是理解這個(gè)操作用公式的三種描述方式（上圖中畫紅線處）

第一種：X*((-k))NRN(k)，是最直觀地展現(xiàn)上述過程的；

第二種：X*((N-k))NRN(k)，可以認(rèn)為是利用其周期性（周期延拓得到的當(dāng)然是以N為周期的啦），把-k換成了N-k；

第三種：去掉了雙括號(hào)，也去掉了RN(k），好像看不出“周期延拓”和“取主值區(qū)間”的操作了。大家會(huì)心存疑慮，這個(gè)等號(hào)成立嗎？

我們用下圖的例子來說明一下這個(gè)等號(hào)成立，為了畫圖的方便，我們用函數(shù)值為實(shí)數(shù)的情況，圖中是以n為自變量，換作k當(dāng)然也是一樣的。

圖2

x(N-n)可以看作簡(jiǎn)寫形式，優(yōu)點(diǎn)在于形式簡(jiǎn)潔明了，缺點(diǎn)在于掩蓋了周期延拓再取主值的過程。用這種簡(jiǎn)寫形式，要注意一點(diǎn)，N點(diǎn)長序列x(n)，n的取值范圍為0≤n≤N-1，也就是說，本來應(yīng)該x(N)=0。但是，此處，當(dāng)n=0時(shí)，x(N-n)=x(N)，不能認(rèn)為x(N)=0，而要認(rèn)為x(N)=x(0)。也就是說，要把x(n)的這N個(gè)點(diǎn)，認(rèn)為是周期序列的主值區(qū)間，那么x(N)就是下一個(gè)周期的第一個(gè)點(diǎn)，所以x(N)=x(0)。

用這種簡(jiǎn)寫形式來描述這個(gè)性質(zhì)，就是：時(shí)域取共軛，對(duì)應(yīng)的DFT，相當(dāng)于把序號(hào)k與序號(hào)N-k做一個(gè)互換，然后取共軛。

下面，看這個(gè)性質(zhì)的兩個(gè)推論。

（2）第一個(gè)推論：實(shí)序列的DFT是圓周共軛對(duì)稱序列。

圖4

（此處省略若干公式）

”圓周共軛對(duì)稱“是個(gè)什么鬼？

我們按照以下幾步來解釋一下：

第一步：從“偶對(duì)稱、奇對(duì)稱”到“共軛對(duì)稱/共軛反對(duì)稱”

偶對(duì)稱/奇對(duì)稱地球人都知道吧。共軛對(duì)稱/反對(duì)稱就不是地球人都知道了，大學(xué)生才知道。

對(duì)于實(shí)函數(shù)x(n)，如果x(-n)=x(n)，稱之為偶對(duì)稱，x(-n)=-x(n)稱之為奇對(duì)稱。

擴(kuò)展到復(fù)函數(shù)x(n)，如果x*(-n)=x(n)，稱之為共軛對(duì)稱，x*(-n)=-x(n)稱之為共軛反對(duì)稱。

第二步：從“共軛對(duì)稱”到“圓周共軛對(duì)稱”

圓周共軛對(duì)稱的定義：對(duì)于N點(diǎn)長序列x(n)，如果x(n)=x((N-n))NRN(n)，或者用簡(jiǎn)寫形式：x(n)=x(N-n)，那么稱之為“圓周共軛對(duì)稱”。

可以理解為：把x(n)放在一個(gè)圓周的N個(gè)等分點(diǎn)上，或者說把橫軸掰彎，彎成一個(gè)圓（n=N-1與原點(diǎn)重合），則這N個(gè)序列值關(guān)于原點(diǎn)對(duì)稱，或者說關(guān)于N/2也對(duì)稱。如下圖所示。

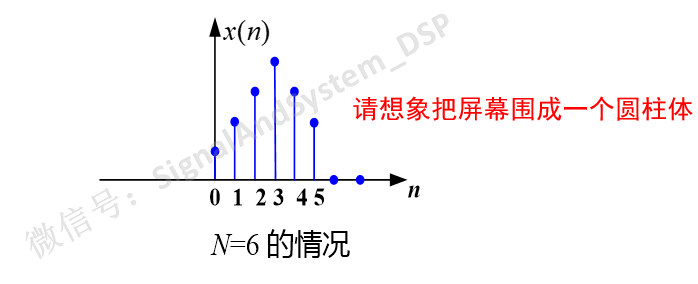
圖5

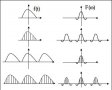
我們前面求解過的例題：5點(diǎn)矩形脈沖的DFT，如下圖，也體現(xiàn)出圓周偶對(duì)稱的特點(diǎn)。

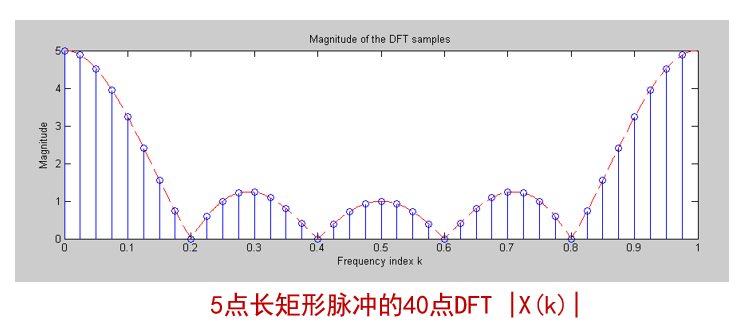
圖6

（3）第二個(gè)推論：實(shí)部/虛部與圓周共軛對(duì)稱/反對(duì)稱分量的關(guān)系

首先解釋一下什么叫圓周共軛對(duì)稱分量和圓周共軛反對(duì)稱分量。需要經(jīng)過以下幾步循序漸進(jìn)的理解。

第一步：函數(shù)可以分解為偶分量+奇分量

圖7

第二步：從“偶分量/奇分量”到“共軛對(duì)稱分量/共軛反對(duì)稱分量”

把（1）式中的x(-n)改為x*(-n)即可

圖8

以上兩式，無論是對(duì)無限長序列，還是有限長序列，都是適用的。如果x(n)為N點(diǎn)長，并且0≤n≤N-1，那么xe(n)和xo(n)是2N-1點(diǎn)長，并且-(N-1)≤n≤N-1。

第三步：改造成適合DFT的

凡是涉及到自變量取負(fù)（也就是反轉(zhuǎn)）的，都加上“周期延拓，再取主值區(qū)間”的操作。也就是把（2）式中的x(-n)改為x((N-n))NRN(n)，用簡(jiǎn)寫形式表示就是x(N-n)

因此，得到圓周共軛對(duì)稱分量和圓周共軛反對(duì)稱分量的定義：

圖9

注意，前提是x(n)為N點(diǎn)長序列，并且n的范圍是0≤n≤N-1，圓周共軛對(duì)稱/反對(duì)稱分量的長度仍是N，n的范圍也不變。而且如前所述，n=0時(shí)，x(N-0)=x(N)=x(0)。

上面，是以x(n)為例，同樣，對(duì)于DFT X(k)，也可以定義圓周共軛對(duì)稱/反對(duì)稱分量，不再贅述。

解釋完這些，我們的核心公式就出來啦（證明過程省略，直接看結(jié)論）。

序列 x(n)及其DFT的實(shí)部/虛部與圓周共軛對(duì)稱/反對(duì)稱分量之間的關(guān)系 ，見下圖：

圖10

（此處省略若干公式）

翻譯成人話（繞口令）就是：

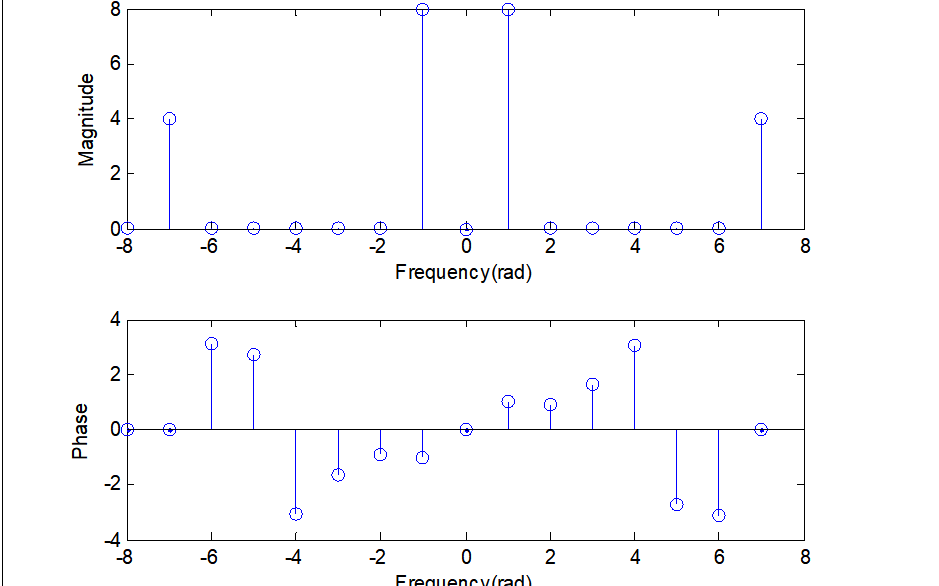
序列實(shí)部的DFT是序列DFT的共軛對(duì)稱分量

序列虛部×j的DFT是序列DFT的共軛反對(duì)稱分量

序列共軛對(duì)稱分量的DFT是序列DFT的實(shí)部

序列共軛反對(duì)稱分量的DFT是序列DFT的虛部×j

是不是像繞口令，但總比公式強(qiáng)多了。

這一切，意義何在？

第一，從圖形上可以淋漓盡致地體現(xiàn)DFT隱含的周期性。

第二，為DFT的簡(jiǎn)化運(yùn)算提供了思路。

4、Parseval定理

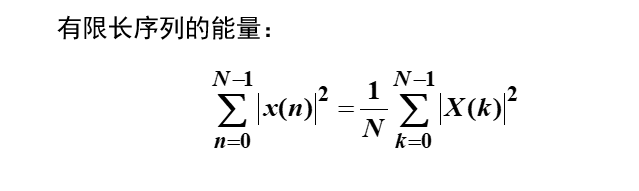
圖11