前言
奇異值分解(SVD)在降維,數(shù)據(jù)壓縮,推薦系統(tǒng)等有廣泛的應(yīng)用,任何矩陣都可以進(jìn)行奇異值分解,本文通過正交變換不改變基向量間的夾角循序漸進(jìn)的推導(dǎo)SVD算法,以及用協(xié)方差含義去理解行降維和列降維,最后介紹了SVD的數(shù)據(jù)壓縮原理 。
1. 正交變換
正交變換公式:
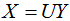
上式表示:X是Y的正交變換,其中U是正交矩陣,X和Y為列向量 。
下面用一個(gè)例子說明正交變換的含義:
假設(shè)有兩個(gè)單位列向量a和b,兩向量的夾角為θ,如下圖:
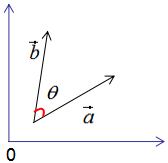
現(xiàn)對向量a,b進(jìn)行正交變換:
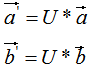
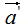 ,
,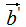 的模:
的模:
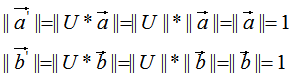
由上式可知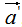 和
和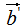 的模都為1。
的模都為1。
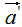 和
和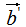 的內(nèi)積:
的內(nèi)積:
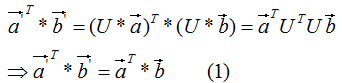
由上式可知,正交變換前后的內(nèi)積相等。
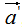 和
和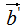 的夾角
的夾角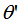 :
:
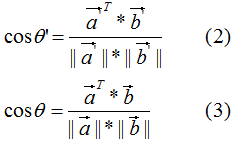
比較(2)式和(3)式得:正交變換前后的夾角相等,即: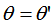
因此,正交變換的性質(zhì)可用下圖來表示:
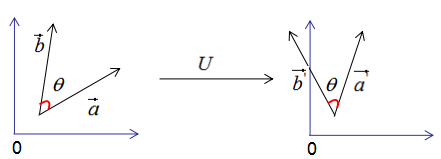
正交變換的兩個(gè)重要性質(zhì):
1)正交變換不改變向量的模。
2)正交變換不改變向量的夾角。
如果向量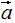 和
和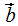 是基向量,那么正交變換的結(jié)果如下圖:
是基向量,那么正交變換的結(jié)果如下圖:
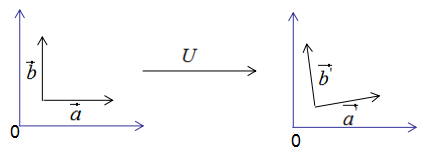
上圖可以得到重要結(jié)論:基向量正交變換后的結(jié)果仍是基向量。基向量是表示向量最簡潔的方法,向量在基向量的投影就是所在基向量的坐標(biāo),我們通過這種思想去理解特征值分解和推導(dǎo)SVD分解。
2. 特征值分解的含義
對稱方陣A的特征值分解為:
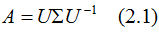
其中U是正交矩陣,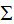 是對角矩陣。
是對角矩陣。
為了可視化特征值分解,假設(shè)A是2×2的對稱矩陣,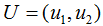 ,
,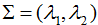 。(2.1)式展開為:
。(2.1)式展開為:
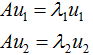
用圖形表示為:
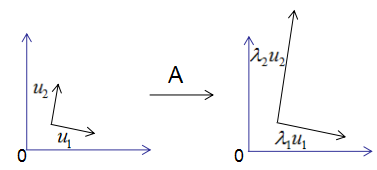
由上圖可知,矩陣A沒有旋轉(zhuǎn)特征向量,它只是對特征向量進(jìn)行了拉伸或縮短(取決于特征值的大小),因此,對稱矩陣對其特征向量(基向量)的變換仍然是基向量(單位化)。
特征向量和特征值的幾何意義:若向量經(jīng)過矩陣變換后保持方向不變,只是進(jìn)行長度上的伸縮,那么該向量是矩陣的特征向量,伸縮倍數(shù)是特征值。
3. SVD分解推導(dǎo)
我們考慮了當(dāng)基向量是對稱矩陣的特征向量時(shí),矩陣變換后仍是基向量,但是,我們在實(shí)際項(xiàng)目中遇到的大都是行和列不相等的矩陣,如統(tǒng)計(jì)每個(gè)學(xué)生的科目乘積,行數(shù)為學(xué)生個(gè)數(shù),列數(shù)為科目數(shù),這種形成的矩陣很難是方陣,因此SVD分解是更普遍的矩陣分解方法。
先回顧一下正交變換的思想:基向量正交變換后的結(jié)果仍是基向量。
我們用正交變換的思想來推導(dǎo)SVD分解:
假設(shè)A是M*N的矩陣,秩為K,Rank(A)=k。
存在一組正交基V:
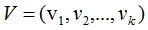
矩陣對其變換后仍是正交基,記為U:
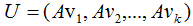
由正交基定義,得:
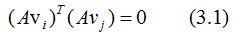
上式展開:
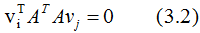

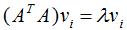
∴ (3.2)式得:
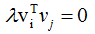
即假設(shè)成立 。
圖形表示如下:
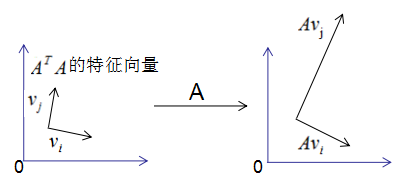
正交向量的模:
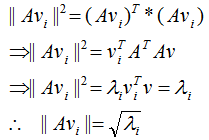
單位化正交向量,得:
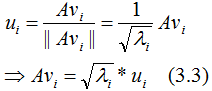
結(jié)論:當(dāng)基向量是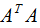 。
。
用矩陣的形式表示(3.3)式:
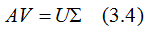
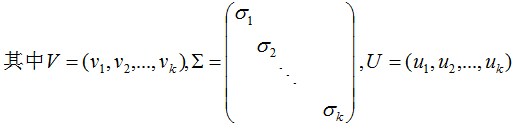
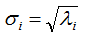
V是N*K矩陣,U是M*K矩陣,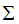 是M*K的矩陣,需要擴(kuò)展成方陣形式:
是M*K的矩陣,需要擴(kuò)展成方陣形式:
將正交基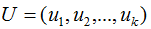 擴(kuò)展
擴(kuò)展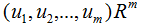 空間的正交基,即U是M*M方陣 。
空間的正交基,即U是M*M方陣 。
將正交基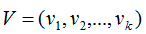 擴(kuò)展成
擴(kuò)展成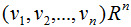 空間的正交基,其中
空間的正交基,其中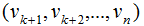 是矩陣A的零空間,即:
是矩陣A的零空間,即:
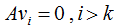
對應(yīng)的特征值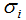 =0,
=0,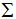 是M*N對角矩陣,V是N*N方陣
是M*N對角矩陣,V是N*N方陣
因此(3.4)式寫成向量形式為:
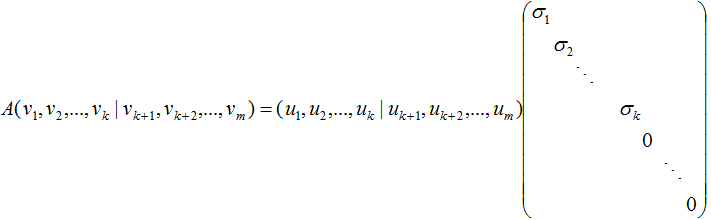
得:
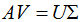
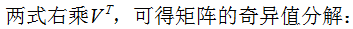
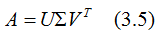
(3.5)式寫成向量形式:
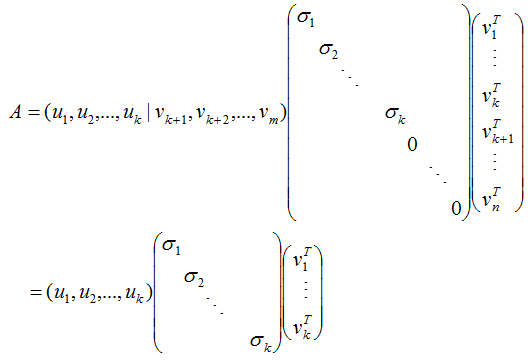
令:
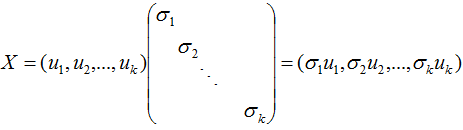
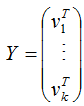
則:
A = XY
因?yàn)閄和Y分別是列滿秩和行滿秩,所以上式是A的滿秩分解。
(3.5)式的奇異矩陣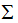 的值
的值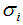 是
是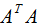 特征值的平方根,下面推導(dǎo)奇異值分解的U和V:
特征值的平方根,下面推導(dǎo)奇異值分解的U和V:
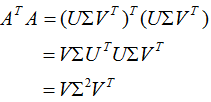
即V是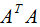 的特征向量構(gòu)成的矩陣,稱為右奇異矩陣。
的特征向量構(gòu)成的矩陣,稱為右奇異矩陣。
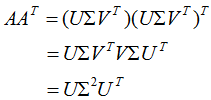
即U是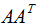 的特征向量構(gòu)成的矩陣,稱為左奇異矩陣 。
的特征向量構(gòu)成的矩陣,稱為左奇異矩陣 。
小結(jié):矩陣A的奇異值分解:
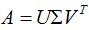
其中U是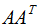 的特征向量構(gòu)成的矩陣,V是
的特征向量構(gòu)成的矩陣,V是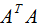 的特征向量構(gòu)成的矩陣,奇異值矩陣
的特征向量構(gòu)成的矩陣,奇異值矩陣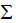 的值是
的值是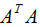 特征值的平方根 。
特征值的平方根 。
3. 奇異值分解的例子
本節(jié)用一個(gè)簡單的例子來說明矩陣是如何進(jìn)行奇異值分解的。矩陣A定義為:
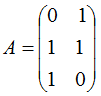
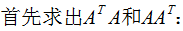
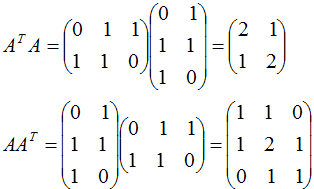
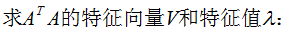

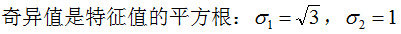
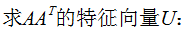
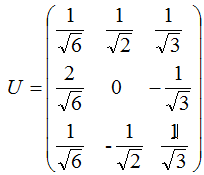
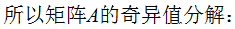
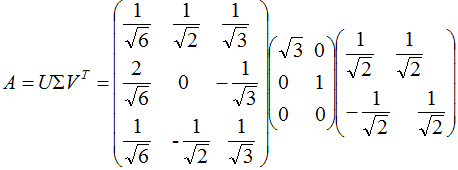
4. 行降維和列降維
本節(jié)通過協(xié)方差的角度去理解行降維和列降維,首先探討下協(xié)方差的含義:
單個(gè)變量用方差描述,無偏方差公式:
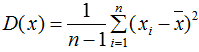

兩個(gè)變量用協(xié)方差描述,協(xié)方差公式:
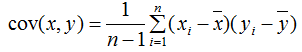
多個(gè)變量(如三個(gè)變量)之間的關(guān)系可以用協(xié)方差矩陣描述:
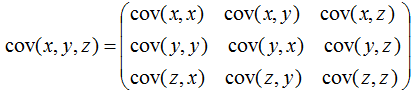
相關(guān)系數(shù)公式:
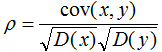
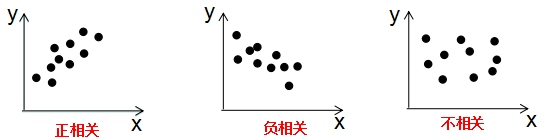
由上式可知,協(xié)方差是描述變量間的相關(guān)關(guān)系程度:
1)協(xié)方差cov(x,y) > 0時(shí),變量x與y正相關(guān);
2)協(xié)方差cov(x,y)<0時(shí),變量x與y負(fù)相關(guān);
3)協(xié)方差cov(x,y)=0時(shí),變量x與y不相關(guān);
變量與協(xié)方差關(guān)系的定性分析圖:
現(xiàn)在開始討論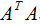 和
和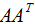 的含義:
的含義:
假設(shè)數(shù)據(jù)集是n維的,共有m個(gè)數(shù)據(jù),每一行表示一例數(shù)據(jù),即:
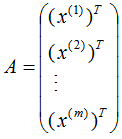
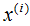 表示第i個(gè)樣本,
表示第i個(gè)樣本,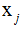
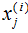 表示第i個(gè)樣本的第j維特征?。
表示第i個(gè)樣本的第j維特征?。
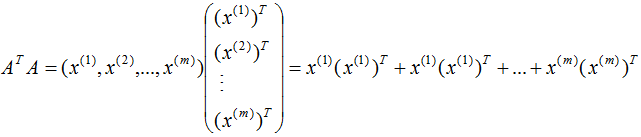
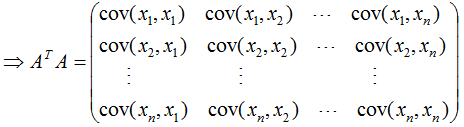
由上式可知,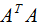 是描述各特征間相關(guān)關(guān)系的矩陣,所以
是描述各特征間相關(guān)關(guān)系的矩陣,所以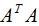 的正交基V是以數(shù)據(jù)集的特征空間進(jìn)行展開的。
的正交基V是以數(shù)據(jù)集的特征空間進(jìn)行展開的。
數(shù)據(jù)集A在特征空間展開為:
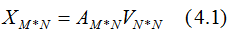
由上一篇文章可知,特征值表示了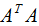 在相應(yīng)特征向量的信息分量。特征值越大,包含矩陣
在相應(yīng)特征向量的信息分量。特征值越大,包含矩陣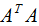 的信息分量亦越大。
的信息分量亦越大。
若我們選擇前r個(gè)特征值來表示原始數(shù)據(jù)集,數(shù)據(jù)集A在特征空間展開為:
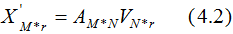
(4.2)式對列進(jìn)行了降維,即右奇異矩陣V可以用于列數(shù)的壓縮,與PCA降維算法一致。
行降維:
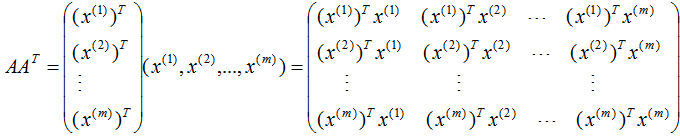
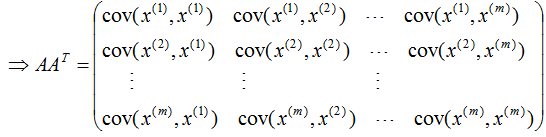
由上式可知: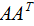 是描述樣本數(shù)據(jù)間相關(guān)關(guān)系的矩陣,因此,左奇異矩陣U是以樣本空間進(jìn)行展開,原理與列降維一致,這里不詳細(xì)介紹了 。
是描述樣本數(shù)據(jù)間相關(guān)關(guān)系的矩陣,因此,左奇異矩陣U是以樣本空間進(jìn)行展開,原理與列降維一致,這里不詳細(xì)介紹了 。
若我們選擇前r個(gè)特征值來表示原始數(shù)據(jù)集,數(shù)據(jù)集A在樣本空間展開為:
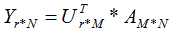
因此,上式實(shí)現(xiàn)了行降維,即左奇異矩陣可以用于行數(shù)的壓縮。
5. 數(shù)據(jù)壓縮
本節(jié)介紹兩種數(shù)據(jù)壓縮方法:滿秩分解和近似分解
矩陣A的秩為k,A的滿秩分解:
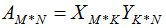
滿秩分解圖形如下:
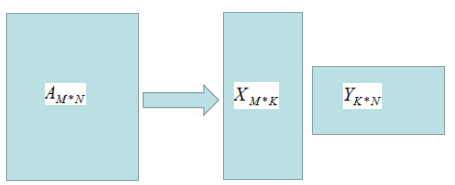
由上圖可知,存儲X和Y的矩陣比存儲A矩陣占用的空間小,因此滿秩分解起到了數(shù)據(jù)壓縮作用。
若對數(shù)據(jù)再次進(jìn)行壓縮,需要用到矩陣的近似分解。
矩陣A的奇異值分解:
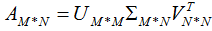
若我們選擇前r個(gè)特征值近似矩陣A,得:
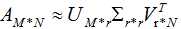
如下圖:
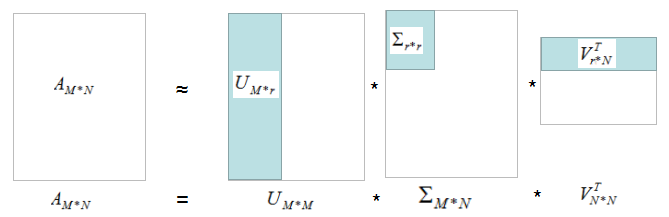
我們用灰色部分的三個(gè)小矩陣近似表示矩陣A,存儲空間大大的降低了。
6. SVD總結(jié)
任何矩陣都能進(jìn)行SVD分解,SVD可以用于行降維和列降維,SVD在數(shù)據(jù)壓縮、推薦系統(tǒng)和語義分析有廣泛的應(yīng)用,SVD與PCA的缺點(diǎn)一樣,分解出的矩陣解釋性不強(qiáng) 。
-
矩陣
+關(guān)注
關(guān)注
1文章
434瀏覽量
35084 -
向量
+關(guān)注
關(guān)注
0文章
55瀏覽量
11860 -
SVD
+關(guān)注
關(guān)注
0文章
21瀏覽量
12302
原文標(biāo)題:奇異值分解(SVD)原理總結(jié)
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區(qū)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
【TL6748 DSP申請】井下數(shù)據(jù)壓縮技術(shù)
數(shù)據(jù)壓縮技術(shù)
高速數(shù)據(jù)壓縮與緩存的FPGA實(shí)現(xiàn)
基于實(shí)時(shí)數(shù)據(jù)庫的數(shù)據(jù)壓縮算法

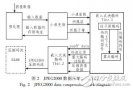
JPEG2000數(shù)據(jù)壓縮的FPGA實(shí)現(xiàn)
JAVA教程之數(shù)據(jù)壓縮與傳輸
小波算法在監(jiān)測數(shù)據(jù)壓縮中的應(yīng)用
基于運(yùn)動(dòng)狀態(tài)改變的GPS軌跡數(shù)據(jù)壓縮算法
數(shù)據(jù)壓縮的重要性
數(shù)據(jù)壓縮算法計(jì)算步驟及過程
有趣!史記:數(shù)據(jù)壓縮算法列傳
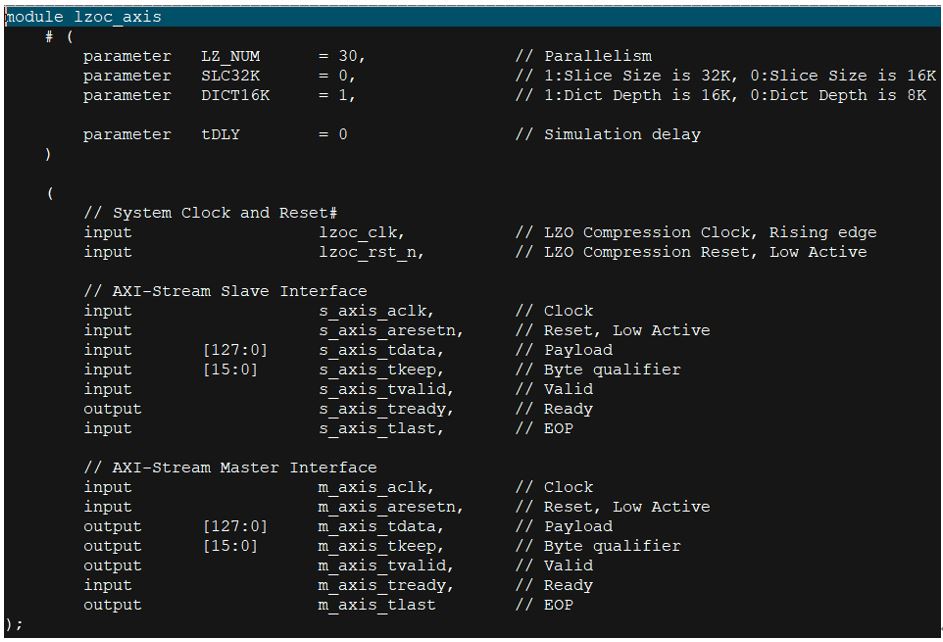
高性能無損數(shù)據(jù)壓縮FPGA IP,LZO無損數(shù)據(jù)壓縮IP





 SVD的數(shù)據(jù)壓縮原理
SVD的數(shù)據(jù)壓縮原理










評論