本文是離散信號的頻域分析(共5節)中的第5節——傅里葉變換的應用的第一篇。
在開始學習之前,提醒大家,本節內容的學習,需要用到前面DTFT、DFT以及FFT的知識。如果前面這些內容沒有掌握的話,那就不具備繼續學習本節內容的條件。當然,本節內容的學習,可以加深對前面這幾個問題的深化理解。

本節內容分為兩部分:5.1FFT分析信號頻譜;5.2FFT實現線性卷積。本文是第一部分:FFT分析信號頻譜。
5.1FFT分析信號頻譜
1. 用FFT實現頻譜分析的基本過程
我們知道,現實世界中的絕大多數物理量都是以連續變化的形式存在的,而做為離散傅里葉變換,只能處理有限長的離散數據。所以對信號進行FFT之前,必須首先將其進行離散化處理并截取合適的長度。
下圖為用FFT實現頻譜分析的基本過程。
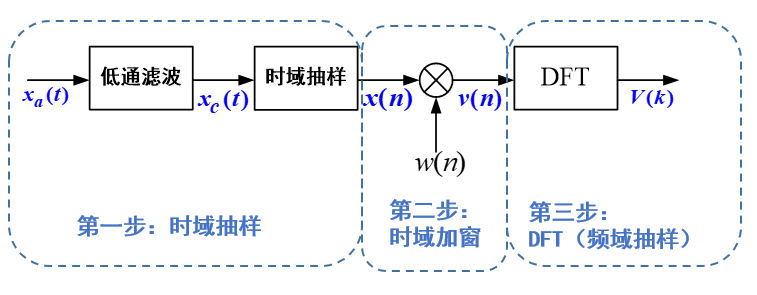
下面我們詳細來看具體每一步對信號做了什么樣的處理,我們重點關注這些處理對信號的頻譜特征有什么樣的影響。
2. 時域抽樣
第一步為時域抽樣,我們已經學習過。其作用是將連續時間信號按照一定的抽樣間隔離散化,得到離散數據。時域抽樣包含兩個過程:
首先,將連續時間信號通過理想低通濾波器,該濾波器又稱為“抗混疊濾波器”,作用是濾除高于抽樣頻率一半的高頻分量,防止抽樣時發生頻譜混疊。
然后,對信號進行抽樣。抽樣后得到離散時間信號x(n),其頻譜,能否代表原來的連續時間信號的頻譜信息呢?
當然能!因為只要滿足抽樣定理,抽樣后的離散數值就可以完全代表原來連續時間信號的信息。但問題是,離散時間信號的頻譜,已經是數字域頻率,攜帶的頻率信息,需要轉換為模擬頻率,如何轉換?
這個問題,本公號前面有文章專門論述,鏈接如下:
數字信號處理系列(離散信號的頻域分析之二)——數字域頻率與模擬角頻率
本文不再重復,只給出結論。

根據上圖的公式反推:
模擬角頻率 = 數字域頻率 * 抽樣頻率fs
3. 時域加窗
下面我們分析第二步——時域加窗。
從三個方面來看:第一,為什么要加窗?第二,怎樣實現加窗?第三,加窗有什么影響?
首先看,為什么要加窗?無他,因為數據太長太多,處理不了啊,臣妾做不到;或者是處理時間太長,臣妾等不及啊。更有甚者,有時輸入信號是無限長的,總不能等到世界末日再去處理吧?
然后看,怎樣實現加窗?
最簡單加窗方式,就是將很長很長的數據,與矩形脈沖RN(n)相乘,就實現了截取n=0~N-1這N個點。RN(n)稱為“矩形窗”。
除了矩形窗,有沒有其他形式的窗呢?有,但這是后話,以后再講。
這里重點分析第三個問題——加窗有什么影響?
先看一般的信號,如下圖所示,頻譜為示意圖。根據“時域相乘,頻域卷積”,加窗后信號的頻譜,是原來的頻譜X(w)與矩形窗的頻譜W(w)做卷積,那么,卷積后的頻譜(也即加窗后的頻譜)是什么樣子呢?和很多因素有關(原始信號的頻譜、窗函數的頻譜、長度等等)。從何處入手來分析呢?
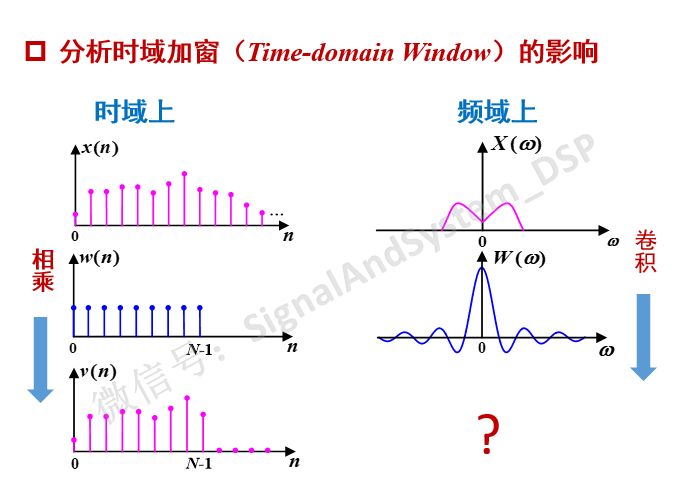
我們知道,正弦信號是基本信號,因為復雜信號可以看是一個個不同頻率的正弦信號組合而成,所以下面首先分析正弦信號。
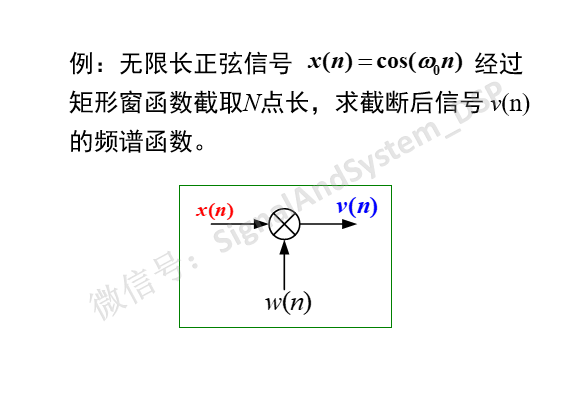
我們知道,無限長正弦信號的頻譜為正負w0處的沖激,如下圖(a),矩形窗的頻譜,如下圖(b)。二者卷積后(也就是N點長的正弦信號)的頻譜,如圖(c)。
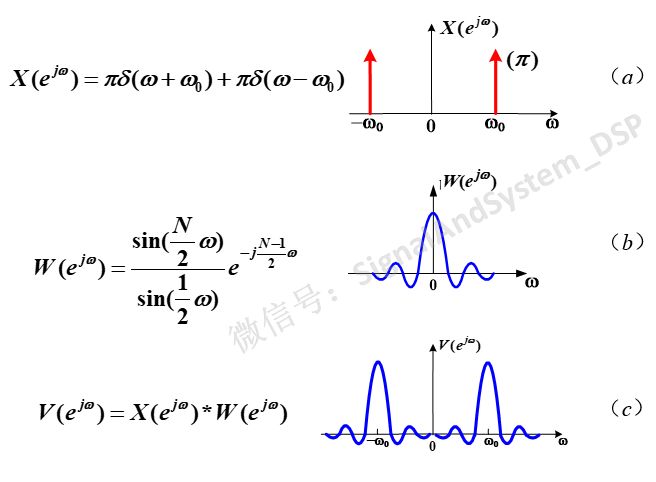
比較圖(a)和圖(c),可以看到,加窗后信號的頻譜與加窗前相比,發生了哪些變化呢?變寬了,原來窄窄的一條(瘦成閃電)變成寬寬的胖子,而且出現起伏的尾巴。
用術語說,就是:
時域加窗,導致頻譜的擴散——拖尾、變寬,稱為頻譜泄漏(Leakage)。
為什么變胖?是因為矩形窗函數的頻譜胖(主瓣)。胖的程度,取決于N。N越小主瓣越寬,則越胖。所以,我們要想減少主瓣泄露,可以適當增大N。
為什么出現尾巴?是因為矩形窗函數的頻譜有起伏(旁瓣)。要想減小旁瓣泄露,就要降低窗函數旁瓣的幅度。
但是,我們知道,矩形窗函數,旁瓣幅度與主瓣幅度之比是一定的(-13dB左右),增大N并不能改變這一數值。那么,如何是好呢?
對數據加矩形窗是我們很自然的行為,因為它不改變截取部分信號的取值。但是矩形窗在起點和終點都是不連續的,也就是說,數據是突然開始、突然結束的。從物理概念上很好解釋,這種時域上的突然變化,意味著頻域上存在高頻分量。如果抑制了這些高頻分量,就能夠降低旁瓣幅度。因此從這樣一個角度,直觀上就可以想到,窗函數的起始處和結束處越平坦,對旁瓣的抑制就應該越好。關于窗函數的內容,我們后面會專門學習。
前面分析了加窗對信號頻譜的影響,總結一句話:時域加窗,會導致頻譜泄露——頻譜展寬、拖尾。同時,我們必須認識到,在進行DFT運算時,時域加窗是必須的,因此泄漏現象是離散傅里葉變換所固有的,無法消除,只能在計算量等容許的范圍內,盡量抑制泄露現象。
4.頻域抽樣(DFT)
經過前面兩步,數據離散化了,也是有限長的了,準備工作終于完成了,可以做DFT了。
DFT,也就是頻域抽樣。其實質就是對信號v(n)的頻譜(DTFT)離散化,[0,2Π]區間上離散化成N個點,就是N點DFT。注意,這個N是指DFT的點數,而不是前文中的信號長度。
v(n)的頻譜也就是上圖中的(c),但我們首先需要把圖(c)變一下。
為什么需要變一下呢?所有離散時間信號的頻譜,都是以2Π為周期的,圖(a)(b)(c)實際上畫出的是-Π~Π區間內的圖形。為了和DFT的研究區間一致([0,2Π]),我們把圖(c)變成[0,2Π]區間,也就是下圖(d)。
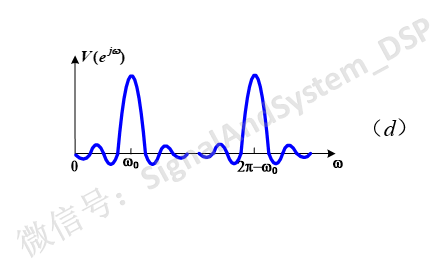
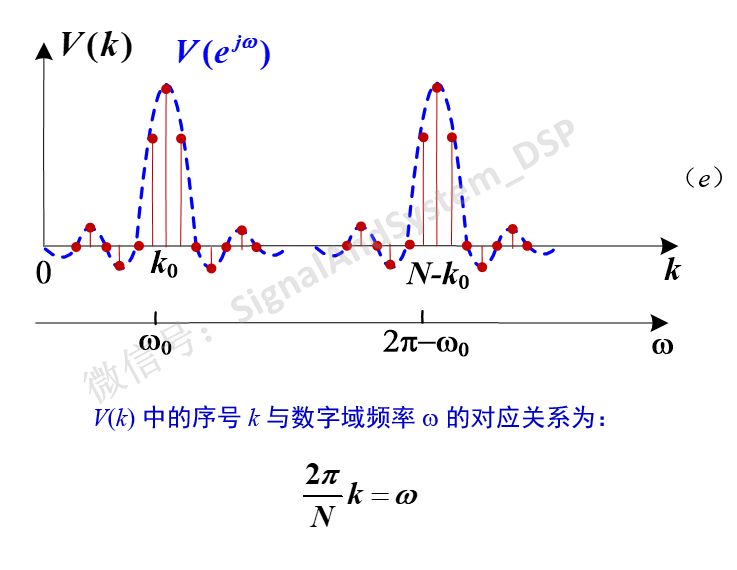
然后,把它以2Π/N為間隔離散化,得到的就是最后的結果V(k)。如下圖(e)所示。
理論分析講完了,最后出一個題。

-
濾波器
+關注
關注
162文章
8139瀏覽量
182143 -
傅里葉變換
+關注
關注
6文章
443瀏覽量
43155 -
離散信號
+關注
關注
0文章
18瀏覽量
7392
原文標題:數字信號處理系列串講第11篇(離散信號的頻域分析之五)——傅里葉變換的應用(1):FFT分析信號頻譜(之一)
文章出處:【微信號:SignalAndSystem_DSP,微信公眾號:信號與系統和數字信號處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄





 離散信號的頻域分析之傅里葉變換的應用
離散信號的頻域分析之傅里葉變換的應用

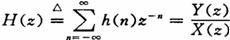










評論