Sallen-Key濾波器拓撲用作實現更高階有源濾波器的構建塊

Sallen和Key Filter設計是一個二階有源濾波器拓撲，我們可以用作實現高階濾波器電路的基本構建模塊，如低通濾波器（LPF），高通濾波器（HPF）和帶通濾波器電路。

As我們已經在這個濾波器部分看到，無源或有源電子濾波器用于僅在有限頻率范圍內需要信號幅度的電路中。使用 Sallen-Key濾波器設計的優勢在于它們易于實現和理解。

Sallen和Key拓撲是一種基于單個非反相的有源濾波器設計運算放大器和兩個電阻，從而創建一個壓控電壓源（VCVS）設計，具有濾波器特性，高輸入阻抗，低輸出阻抗和良好的穩定性，因此允許單獨的Sallen鍵濾波器部分級聯到一起產生更高階的濾波器。

但在我們看一下 Sallen-key濾波器的設計和操作之前，讓我們首先提醒自己一個電阻器 - 電容器的特性，當受到一系列輸入頻率時，RC網絡或RC網絡。

分壓器

當兩個（或更多）電阻器在一個直流電源電壓上連接在一起時，不同的電壓值將是在每個電阻器上產生，產生基本上稱為分壓器或壓電器的電阻器分壓器網絡。

電阻分壓器

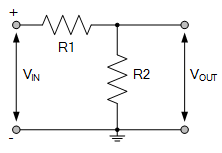
所示基本電路由兩個串聯電阻串聯電壓， V IN 。

歐姆定律告訴我們電阻上的電壓降是電流的總和流經它的電阻值乘以電阻值V = I * R，所以如果兩個電阻相等，那么兩個電阻上的電壓下降， R1 和 R2 也會在電阻 R2 之間產生或下降的電壓代表輸出電壓， V OUT

span>由兩個電阻和輸入電壓的比值給出。因此，這個簡單的分壓器網絡的傳遞函數如下：

電阻分壓器傳遞函數

但是如果我們將輸入電壓改為交流電源或信號并改變其頻率范圍，輸出電壓 V OUT 會發生什么。實際上沒什么，因為電阻通常不受頻率變化（排除線繞）的影響，因此它們的頻率響應為零，允許AC，Irms 2 * R電壓在電阻器上產生或下降與穩態直流電壓相同。

RC分壓器

如果我們將電阻器 R1 更改為電容器， C 如圖所示，這將如何影響我們之前的傳遞函數。我們從有關電容器的教程中了解到，當連接到直流電源時，電容的行為就像開路一樣。

RC分壓器

因此，當穩態直流電源連接到 V IN 時，電容器將在5個時間常數（5T = 5RC）后充滿電，在這段時間內，它不會從電源中吸取電流。因此沒有電流流過電阻器 R 并且沒有電壓降產生，因此沒有輸出電壓。換句話說，電容器一旦充電就會阻止穩態直流電壓。

如果我們現在將輸入電源改為交流正弦電壓，這個簡單的RC電路的特性會完全隨著直流或恒定部分而變化。信號被阻止。所以現在我們正在分析頻域中的RC電路，這是信號中依賴于時間的部分。

在交流電路中，電容具有容抗電容電抗

b>，X C但我們仍然可以用與電阻電路相同的方式分析RC電路，區別在于電容器的阻抗現在取決于頻率。

對于交流電路和信號，容抗（ X C ），是對交替的反對電流以歐姆為單位流過電容器。電容電抗是頻率相關的，即在低頻率（??0）時電容表現得像開路并阻塞它們

在非常高的頻率（??∞）下，電容表現得像一個短路，并將信號直接傳遞給輸出，因為 V OUT = V <子> IN 。然而，在這兩個極端頻率之間的某處，電容器具有由 X C 給出的阻抗。所以我們的上面的分壓器傳遞函數變為：

因此頻率的變化會導致的變化X C ，這會導致輸出電壓幅度的變化。考慮下面的電路。

RC濾波電路

圖表顯示了頻率響應這個簡單的1 st - 階RC電路。在低頻時，電壓增益非常低，因為輸入信號被電容器的電抗阻擋。在高頻時，電壓增益很高（單位），因為電抗會使電容器有效地成為這些高頻的短路，因此 V OUT = V IN

然而，變頻器的電抗等于電阻的電阻的頻率點，即： X C = R ，這稱為“臨界頻率”點，或更常稱為截止頻率，或轉角頻率? C。

當 X C = R時發生截止頻率用于計算此臨界頻率點的標準公式如下：

截止頻率方程

截止頻率? C 定義電路在此示例中從衰減或阻塞以下所有頻率的位置變化， ? C 并開始通過所有頻率ab ove ? C 點。因此，該電路稱為“高通濾波器”。

截止頻率是輸入到輸出信號的比值為0.707，當轉換為分貝時等于 - 3分貝。這通常被稱為濾波器3dB下降點。

由于電容器的電抗與頻率有關，即容抗（ X C ）與施加的頻率成反比，我們可以修改上面的分壓器方程，得到這個簡單的RC高通濾波器電路的傳遞函數，如圖所示。

RC濾波電路

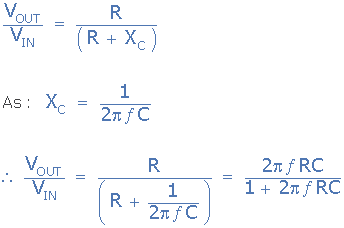
RC濾波器的一個主要缺點是輸出幅度總是小于輸入，所以它永遠不會大于1 。此外，更多RC級或電路對輸出的外部負載將對濾波器特性產生影響。解決此問題的一種方法是通過在基本RC配置中添加運算放大器將無源RC濾波器轉換為“有源RC濾波器”。

通過添加運算放大器，基本RC濾波器可以是設計用于在其輸出端提供所需的電壓增益，從而將濾波器從衰減器改變為放大器。此外，由于運算放大器的高輸入阻抗和低輸出阻抗，可以防止濾波器的外部負載，從而可以在很寬的頻率范圍內輕松調節，而不會改變設計的頻率響應。

考慮簡單的有源下面的RC高通濾波器。

有源高通濾波器

RC濾波器電路的一部分響應與上述相同，即通過高頻但阻擋低頻，截止頻率由R和C的值設定。運算放大器或簡稱運算放大器配置為非反相放大器，其電壓增益由兩個電阻的比率設定， R 1 和 R 2 。

然后非反相運算放大器的通帶中的閉環電壓增益 A V 為：

截止頻率方程

RC濾波器示例No1

A簡單的1 st 階有源高通濾波器要求截止頻率為500Hz，通帶增益為9dB。假設使用標準的741運算放大器，計算所需的元件。

從上面我們已經看到截止頻率? C 被確定通過頻率選擇RC電路中的 R 和 C 的值。如果我們假設 R 的值為5kΩ（任何合理的值都可以），那么 C 的值計算如下：

C 的計算值為63.65nF，因此最接近的首選值為62nF。

通帶區域中高通濾波器的增益為+ 9dB，相當于電壓增益， A V 為2.83。假設反饋電阻的任意值， R 1 為15kΩ，這給出了電阻 R 1 的值：

R 2 的計算值>是8197Ω。最接近的優選值為8200Ω或8.2kΩ。然后，這為我們的有源高通濾波器示例提供了最終電路：

高通濾波器電路

我們已經看到，可以使用單個電阻和電容產生一個簡單的一階高通濾波器，產生一個截止頻率? C 輸出幅度從輸入幅度向下-3dB的點。通過向第一個RC濾波器級添加第二個RC濾波器級，我們可以將電路轉換為二階高通濾波器。

二階RC濾波器

最簡單的二階RC濾波器由兩個RC部分組成，如圖所示。但是，為了使這種基本配置正常工作，兩個RC級的輸入和輸出阻抗不應影響彼此的操作，即它們應該是非相互作用的。

高通濾波器電路

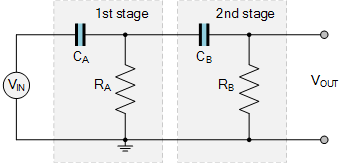
將一個RC濾波器級與另一個（相同或不同的RC值）級聯，因為每個連續階段都不能很好地工作加載前一個RC級，當添加更多RC級時，截止頻率點進一步遠離設計或要求的頻率。

克服無源濾波器設計這個問題的一種方法是使用第二RC級的輸入阻抗至少比第一RC級的輸出阻抗大10倍。即 R B = 10 * R 1 和 C B = C A / 10 在截止頻率處。

將元件值增加10倍的優點是得到的二階濾波器產生更陡峭的滾降比級聯RC級40dB /十倍。但是如果你想設計一個4 th 或6 th -order過濾器，那么計算十倍于前面組件的值可能是耗時且復雜的。

將RC過濾器級聯在一起的一種簡單方法，它們不相互作用或相互加載以創建更高階的過濾器（各個過濾器部分不必相同），可以輕松調整和設計以提供所需的電壓增益是使用 Sallen-key Filter 階段。

Sallen和Key Filters

Sallen-Key是設計一階（1 st -order）的最常見過濾器配置之一和二階（2 nd - 階）濾波器，因此用作創建更高階濾波器的基本構建塊。

Sallen-key的主要優點過濾器設計是：

簡潔和理解他們的基本設計

使用非反相用于提高電壓增益的放大器

一階和二階濾波器設計可以輕松級聯在一起

低通和高通階段可以一起級聯

每個RC級可以有不同的電壓增益

RC組件和放大器的復制

二階Sallen-key平臺比級聯RC具有陡峭的40dB /十倍滾降

然而，基本Sallen-key濾波器存在一些限制設計的原因是電壓增益 A V 和放大系數 Q 由于在Sallen中使用運算放大器而密切相關關鍵設計。幾乎任何大于0.5的 Q 值都可以實現，因為使用非反相配置，電壓增益 A V 將始終大于1，（單位）但必須小于3否則會變得不穩定。

最簡單的Sallen-key濾波器設計形式是使用相等的電容和電阻值（但C和R不是必須相等），運算放大器配置為單位增益緩沖器，如圖所示。請注意，電容 R A 不再接地，而是為放大器提供正反饋路徑。

Sallen-key高通濾波器電路

被動組件 C A ， R A ， C B 和 R B 形式二階頻率選擇電路。因此，在低頻時，電容 C A 和 C B 顯示為開路，因此輸入信號被阻塞導致無輸出。在較高頻率下， C A 和 C B 在正弦輸入信號中顯示為短路，因此信號直接緩沖到輸出。

但是，在截止頻率點附近， C A 和 C B 與 R A 和 R B 的值相同，如上所述，通過 C B 產生的正反饋提供電壓增益，并增加輸出信號放大率， Q 。

由于我們現在有兩組RC網絡，Sallen-Key濾波器的截止頻率的上述公式也被修改：

Sallen-key截止頻率方程

如果兩個串聯電容 C A 且 C B 相等（ C A = C B = C ）和兩個電阻器 R A 和 R B 也相等（ R A = R B = R ），然后上面的等式簡化為原始截止頻率方程：

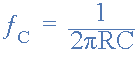
由于運算放大器配置為單位增益緩沖器，即 A = 1 ，截止頻率? C 和 Q 完全相互獨立，從而實現更簡單的濾波器設計。然后放大系數 Q 計算如下：

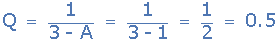
因此對于統一-gain緩沖器配置，濾波器電路的電壓增益（ A V ）在截止頻率點等于0.5或-6dB（過阻尼），我們希望看到這個，因為它是一個二階濾波器響應，為0.7071 * 0.7071 = 0.5。那就是-3dB * -3dB = -6dB。

然而，由于 Q 的值決定了濾波器的響應特性，正確選擇了運算放大器的兩個反饋電阻， R 1 和 R 2 ，允許我們選擇所需的通帶增益 A 對于選定的放大系數， Q 。

請注意，對于Sallen-key濾波器拓撲，選擇 A 的值非常接近最大值3將導致高 Q 值。高 Q 將使濾波器設計對反饋電阻 R 1 和 R 2的容差變化敏感 。例如，將電壓增益設置為2.9（A = 2.9）將導致 Q 的值為10（1 /（3-2.9）），因此濾波器在周圍變得非常敏感? C 。

Sallen-key Filter Response

然后我們可以看到 Q 的值越低，Sallen和Key濾波器設計就越穩定。雖然 Q 的高值會使設計不穩定，但是增益非常高會產生負 Q 會導致振蕩。

Sallen和Key Filter示例No2

設計具有以下特征的二階高通 Sallen和Key Filter 電路：? C = 200Hz 和 Q = 3

為了簡化數學運算，我們假設兩個串聯電容 C A 和 C B 相等（ C A = C B = C ）并且兩個電阻 R A 和 R B 相等（ R A = R <子>乙 = R ）

R 的計算值為7957Ω，因此最接近的首選值為8kΩ。

對于 Q = 3 ，增益計算如下：

如果 A = 2.667 ，那么 R 1 / R <子> 2 = 1.667 如圖所示。

R 2的計算值 為5998Ω，因此最接近的首選值使用6000Ω或6kΩ。然后，這為我們的Sallen和Key高通濾波器示例提供了最終電路：

Sallen和Key High Pass濾波器

然后截止或轉角頻率為200Hz，通帶增益為2.667，截止頻率為8（2.667 * 3）時的最大電壓增益= 3，我們可以在下面的Bode圖中顯示這個二階高通Sallen和Key濾波器的特征。

Sallen和Key Filter Bode Plot

Sallen和Key Filter Summary

我們在本教程中已經看到Sallen-Key配置，也稱為電壓控制，電壓源（VCVS）電路是最廣泛使用的濾波器拓撲結構，主要是因為其設計中使用的運算放大器可配置為單位增益緩沖器或非反相放大器。

基本的Sallen-key濾波器配置可用于實現不同的濾波器響應，例如，Butterworth， Chebyshev，或貝塞爾正確選擇RC濾波器網絡。可以使用 R 和 C 的大多數實際值，記住對于特定的截止頻率點， R 和的值R 成反比。也就是說， R 的值變小， C 變大，反之亦然。

Sallen-key是2 nd - 階濾波器設計，可以與其他RC階段級聯，以創建更高階的濾波器。多個濾波器級不需要相同，但可以各自具有不同的截止頻率或增益特性。例如，將低通階段和高通階段組合在一起以創建Sallen和Key帶通濾波器。

這里我們研究設計一個Sallen-key高通濾波器，但同樣的規則同樣適用于低通設計。電壓增益 A V 決定其響應并由分壓電阻設置， R 1 和 R 2 記住電壓增益必須小于3否則，濾波器電路將變得不穩定。