二進制到十進制數字轉換使用加權列來標識數字的順序以確定數字的最終值
將二進制轉換為十進制(base-2到base-10) )數字和背面是一個重要的概念,因為二進制編號系統構成了所有計算機和數字系統的基礎。
十進制或“denary”計數系統使用Base-of-10編號系統,其中數字中的每個數字都取10個可能值中的一個,稱為“數字”,從 0 到 9 ,例如。 213 10 (二百一十三)。
但是,除了10位數(0到9)之外,十進制編號系統還具有加法運算( + ),減法( - ),乘法(×)和除法(÷)。
在十進制系統中,每個數字的值都比其前一個數字大十倍,這個十進制數字系統使用一組符號 b ,以及一個基數 q ,確定一個數字內每個數字的權重。例如,六十分之六的權重低于六百分之六。然后在二進制編號系統中,我們需要一些方法將十進制轉換為二進制以及從二進制轉換為十進制。
任何編號系統都可以通過以下關系總結:
| N = b i q i | |
| where: |
N 是一個實數正數 b 是數字 是基數值 和整數( i )可以是正數,負數或零 |
N = b n q n ... b'的子> 3 q 3 + b <子> 2 q 2 + b <子> 1 q 1 + b <子> 0 q 0 + b <子> -1 q -1 + b -2 q -2 ... etc。
十進制編號系統
在十進制中, base-10(den)或denary編號系統,當我們沿著從右到左的數字移動時,每個整數列具有單位,數十,數百,數千等的值。在數學上,這些值寫為10 0 ,10 1 ,10 2 ,10 3 等。然后每個位置在小數點左邊表示增加的正冪為10.同樣,對于小數,當我們從左向右移動時,數字的權重變得更負,10 -1 ,10 -2 ,10 -3 等
所以我們可以看到“十進制編號系統”的基數為10或 modulo-10 (有時稱為MOD-10),十進制系統中每個數字的位置表示該數字的大小或重量為 q 等于“10”(0到9)。例如,20(二十)與說2 x 10 1 相同,因此400(四百)與說4 x 10 2 相同。
任何十進制數的值將等于其數字之和乘以各自的權重。例如: N = 6163 10 (六千一百六十三)十進制格式等于:
6000 + 100 + 60 + 3 = 6163
或者可以寫出反映每個數字的權重:
(6×1000)+(1×100)+(6×10)+(3×1)= 6163
或它可以用多項式形式寫成:
(6×10 3 )+(1×10 2 )+(6× 10 1 )+(3×10 0 )= 6163
在此十進制編號系統示例中,最左邊的數字是最高有效數字或MSD,最右邊的數字是最低有效數字或LSD。換句話說,數字 6 是MSD,因為它的最左側位置承載的權重最大,而數字 3 是LSD,因為它的最右側位置承載的權重最小。
二進制編號系統
二進制編號系統是所有基于數字和計算機的系統中最基本的編號系統,二進制數遵循相同的設置規則作為十進制編號系統。但是與使用10的冪的十進制系統不同,二進制編號系統使用2的冪,給出從base-2到base-10的二進制到十進制的轉換。
數字邏輯和計算機系統僅使用兩個用于表示條件,邏輯電平“1”或邏輯電平“0”的值或狀態,并且每個“0”和“1”被認為是2的基數(bi)中的單個數字或“二進制編號系統“。
在二進制編號系統中,二進制數字如 101100101 用字符串”1“和”0“表示,每個數字沿字符串從右到左的值是前一個數字的兩倍。但由于它是二進制數字,因此它只能具有“1”或“0”的值,因此 q 等于“2”(0或1),其位置表示其重量字符串。
由于十進制數是一個加權數,從十進制轉換為二進制(基數10到基數2)也會產生加權二進制數,右邊最多位為最低有效位或LSB,最左邊的位是最高有效位或MSB,我們可以代表這個:
二進制數的表示
| MSB | 二進制數字 | LSB | ||||||
| 2 8 | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
我們在上面看到,在十進制數系統中,每個數字從右到左的權重增加了10倍。在二進制數系統中,權重如圖所示,每個數字增加了一個因子 2 。然后第一個數字的權重為 1 ( 2 0 ),第二個數字的權重為 2 ( 2 1 ),第三個是 4 的重量( 2 2 ) ,第四個是 8 ( 2 3 )的權重,依此類推。
例如,轉換二進制到十進制數字將是:
| 十進制數字值 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 二進制數字值 | 1 | 0 | 1 | <跨度> 1 | 0 | 0 | <跨度> 1 | 0 | 1 |
加在一起在由“ 1 ”表示的位置從右到左的所有十進制數值給出:(256)+(64)+(32)+(4)+(1)= 357 10 或三百五十七作為十進制數。
然后,我們可以通過查找二進制的十進制等效值將二進制轉換為十進制數字數組 101100101 2 并將二進制數字擴展為基數為 2 的系列,其等效值為 357 10 十進制或否定。
請注意,在數字轉換系統中,“下標”用于表示相關的基本編號系統,1001 2 = 9 10 。如果在數字后沒有使用下標,則通常假設成為小數。
重復除2方法
我們已經看到上面如何將二進制數轉換為十進制數,但我們如何將十進制數轉換為二進制數。將十進制數轉換為二進制數等效的簡單方法是寫下十進制數并連續除以2(二)得到結果,并給出“1”或“0”的余數直到最終結果等于零。
例如。將十進制數 294 10 轉換為等效的二進制數。
| Number | 294 |
如圖所示,將每個十進制數除以“2”將得到一個結果加上一個余數。 如果被分割的十進制數是偶數,那么結果將是整數并且余數將等于“0”。如果十進制數是奇數,那么結果將不會完全分割,余數將為“1”。 二進制結果是通過將所有余數按最低有效位(LSB)排序得到的位于頂部,最重要位(MSB)位于底部。 |
|
| 除以2 | |||
| 結果 | 147 | 余數 | 0(LSB) |
| 除以2 | |||
| 結果 | 73 | 余數 | 1 |
| 除以2 | |||
| 結果 | 36 | 余數 | 1 |
| 除以2 | |||
| 結果 | 18 | 余數 | 0 |
| 除以2 | |||
| 結果 | 9 | 余數 | 0 |
| 除以2 | |||
| 結果 | 4 | 余數 | 1 |
| 除以2 | |||
| 結果 | 2 | 余數 | 0 |
| 除以2 | |||
| 結果 | 1 | 余數 | 0 |
| 除以2 | |||
| 結果 | 0 | 余數 | 1(MSB) |
這種除以2的十進制到二進制轉換技術給出十進制數 294 10 相當于 100100110 2 二進制,從右到左閱讀。這種2分頻方法也適用于轉換為其他數字基礎。
然后我們可以看到二進制編號系統的主要特征是每個“二進制數字” “或”位“具有”1“或”0“的值,每個位的權重或值是從最低位或最低位(LSB)開始的前一位的兩倍,這稱為”總和“權重“方法。
因此我們可以通過使用權重和方法或使用重復的2分頻方法將十進制數轉換為二進制數,并將二進制數轉換為十進制通過查找其權重和。
二進制數字名稱&amp;前綴
二進制數可以加在一起,也可以像十進制數一樣減去,結果根據所使用的位數組合成幾個大小范圍之一。二進制數有三種基本形式 - 位,字節和字,其中一位是單個二進制數字,一個字節是八位二進制數字,一個字是16位二進制數字。
分類將各個位分成更大的組通常由以下更常見的名稱引用:
| 二進制數字位數(位) ) | 通用名稱 |
| 1 | 位 |
| 4 | 半字節 |
| 8 | 字節 |
| 16 | Word |
| 32 | 雙字 |
| 64 | Quad Word |
此外,從 Binary轉換為Decimal 或甚至從 Decimal轉換為Binary ,我們需要注意不要混淆兩組數字。例如,如果我們在頁面上寫入數字10,如果我們假設它是十進制數字,它可能意味著數字“十”,或者它可能同樣是二進制中的“1”和“0”,這是等于上面加權十進制格式中的數字2。
在將二進制數轉換為十進制數并確定所使用的數字或數字是十進制數還是二進制數時,要克服此問題的一種方法是在最后一位數字后寫一個稱為“下標”的小數字,以顯示該數字的基數正在使用的數字系統。
因此,例如,如果我們使用二進制數字串,我們將添加下標“2”來表示基數為2,因此數字將寫為 10 <子> 2 。同樣,如果它是標準十進制數,我們將添加下標“10”來表示基數為10的數字,因此該數字將寫為 10 10 。
今天,隨著微控制器或微處理器系統變得越來越大,現在將各個二進制數字(位)組合成8個,形成單個 BYTE 與大多數計算機硬件如硬驅動器和內存模塊通常以兆字節或甚至千兆字節表示其大小。
| 字節數 | 通用名稱 |
| 1,024(2 10 ) | 千字節(kb) |
| 1,048,576(2 20 ) | 兆字節(Mb) |
| 1,073,741,824(2 30 ) | 技嘉(Gb) |
| a非常長的數字!(2 40 ) | 太字節(Tb) |
二進制到十進制摘要
A“ BIT “是源自 BI nary digi T
十進制系統使用10個不同的數字,0到9給它一個10的基數
二進制數是加權值從右到左增加的加權數
二進制數字的權重從右到左翻倍
十進制數可以通過使用權重和方法或重復的二分法來轉換為二進制數
當我們轉換時數字從二進制到十進制,或十進制到二進制,下標用于避免錯誤
將二進制轉換為十進制(base-2到base-10)或十進制到二進制數(base10到base) -2)可以通過如上所示的多種不同方式完成。將十進制數轉換為二進制數時,重要的是要記住哪個是最低有效位( LSB ),哪個是最高有效位( MSB )。
在下一個關于二進制邏輯的教程中,我們將研究將二進制數轉換為十六進制數,反之亦然,并顯示二進制數可以用字母和數字表示。
-
二進制
+關注
關注
2文章
807瀏覽量
42345 -
十進制
+關注
關注
0文章
67瀏覽量
13554
發布評論請先 登錄


十進制和二進制之間的轉換原理
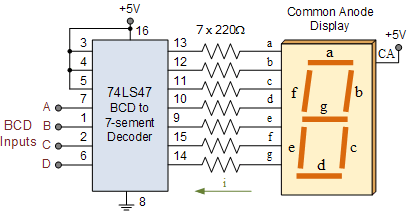
PIC16f877a MPlab組件 ADC結果顯示在七段
二進制與十進制數對照顯示實驗,十進制,二進制對照
二進制編碼的十進制表示轉換解碼器





 二進制如何轉換為十進制?
二進制如何轉換為十進制?











評論