熱敏電阻的基本特性詳細介紹
?電阻-溫度特性
熱敏電阻的電阻-溫度特性可近似地用式1表示。
(式1) R=Ro exp {B(I/T-I/To)}
| R | : 溫度T(K)時的電阻值 |
| Ro | : 溫度T0(K)時的電阻值 |
| B | : B 值 |
| *T(K)= t(oC)+273.15 | |
但實際上,熱敏電阻的B值并非是恒定的,其變化大小因材料構成而異,最大甚至可達5K/°C。因此在較大的溫度范圍內(nèi)應用式1時,將與實測值之間存在一定誤差。
此處,若將式1中的B值用式2所示的作為溫度的函數(shù)計算時,則可降低與實測值之間的誤差,可認為近似相等。
(式2) BT=CT2+DT+E
上式中,C、D、E為常數(shù)。
另外,因生產(chǎn)條件不同造成的B值的波動會引起常數(shù)E發(fā)生變化,但常數(shù)C、D 不變。因此,在探討B(tài)值的波動量時,只需考慮常數(shù)E即可。
?? 常數(shù)C、D、E的計算
常數(shù)C、D、E可由4點的(溫度、電阻值)數(shù)據(jù) (T0, R0). (T1, R1). (T2, R2) and (T3, R3),通過式3~6計算。
首先由式樣3根據(jù)T0和T1,T2,T3的電阻值求出B1,B2,B3,然后代入以下各式樣。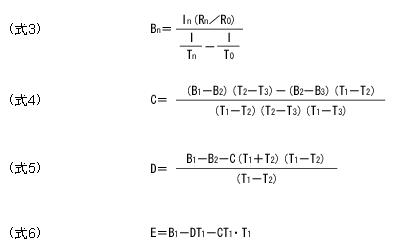
?? 電阻值計算例
試根據(jù)電阻-溫度特性表,求25°C時的電阻值為5(kΩ),B值偏差為50(K)的熱敏電阻在10°C~30°C的電阻值。
?? 步 驟
(1) 根據(jù)電阻-溫度特性表,求常數(shù)C、D、E。
To=25+273.15???T1=10+273.15???T2=20+273.15???T3=30+273.15(2) 代入BT=CT2+DT+E+50,求BT。
(3) 將數(shù)值代入R=5exp {(BTI/T-I/298.15)},求R。
*T : 10+273.15~30+273.15
?? 電阻-溫度特性圖如圖1所示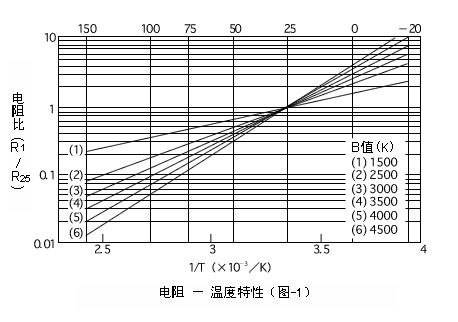
所謂電阻溫度系數(shù)(α),是指在任意溫度下溫度變化1°C(K)時的零負載電阻變化率。電阻溫度系數(shù)(α)與B值的關系,可將式1微分得到。![]()
這里α前的負號(-),表示當溫度上升時零負載電阻降低。
散熱系數(shù) (JIS-C2570)
散熱系數(shù)(δ)是指在熱平衡狀態(tài)下,熱敏電阻元件通過自身發(fā)熱使其溫度上升1°C時所需的功率。
在熱平衡狀態(tài)下,熱敏電阻的溫度T1、環(huán)境溫度T2及消耗功率P之間關系如下式所示。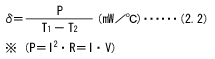
產(chǎn)品目錄記載值為下列測定條件下的典型值。
| (1) | 25°C靜止空氣中。 |
| (2) | 軸向引腳、經(jīng)向引腳型在出廠狀態(tài)下測定。 |
額定功率(JIS-C2570)
在額定環(huán)境溫度下,可連續(xù)負載運行的功率最大值。
產(chǎn)品目錄記載值是以25°C為額定環(huán)境溫度、由下式計算出的值。
(式) 額定功率=散熱系數(shù)×(最高使用溫度-25)
最大運行功率=t×散熱系數(shù) … (3.3)
這是使用熱敏電阻進行溫度檢測或溫度補償時,自身發(fā)熱產(chǎn)生的溫度上升容許值所對應功率。(JIS中未定義。)容許溫度上升t°C時,最大運行功率可由下式計算。
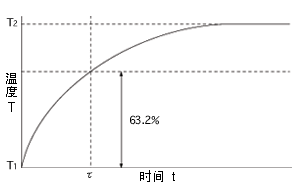
指在零負載狀態(tài)下,當熱敏電阻的環(huán)境溫度發(fā)生急劇變化時,熱敏電阻元件產(chǎn)生最初溫度與最終溫度兩者溫度差的63.2%的溫度變化所需的時間。
熱敏電阻的環(huán)境溫度從T1變?yōu)門2時,經(jīng)過時間t與熱敏電阻的溫度T之間存在以下關系。
| T= | (T1-T2)exp(-t/τ)+T2......(3.1) |
| (T2-T1){1-exp(-t/τ)}+T1.....(3.2) |
上式中,若令t=τ時,則(T-T1)/(T2-T1)=0.632。
換言之,如上面的定義所述,熱敏電阻產(chǎn)生初始溫度差63.2%的溫度變化所需的時間即為熱響應時間常數(shù)。
經(jīng)過時間與熱敏電阻溫度變化率的關系如下表所示。
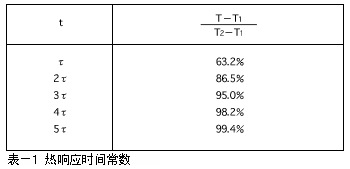
產(chǎn)品目錄記錄值為下列測定條件下的典型值。
| (1) | 靜止空氣中環(huán)境溫度從50°C至25°C變化時,熱敏電阻的溫度變化至34.2°C所需時間。 |
| (2) | 軸向引腳、徑向引腳型在出廠狀態(tài)下測定。 |
另外應注意,散熱系數(shù)、熱響應時間常數(shù)隨環(huán)境溫度、組裝條件而變化。
NTC負溫度系數(shù)熱敏電阻R-T特性?
?
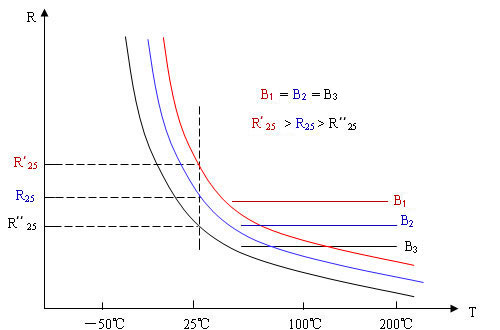
???
B 值相同, 阻值不同的 R-T 特性曲線示意圖?
?
相同阻值,不同B值的NTC熱敏電阻R-T特性曲線示意圖
