如何才能使 A/D 轉換器實現最高性能呢?明顯的答案就是采用良好的設計和板面布局,除此之外,我們還可采用其他技術獲得性能提升。我們實際上可采用一些簡單的技術來推動 A/D 轉換器性能,使之優于規范的要求。為了實現這一點,我們應了解 A/D 轉換器誤差的來源和類型。
本文的目的是解釋 A/D 轉換器最常見的誤差源,并介紹進行上述誤差補償的方法。某些誤差補償的方法理解和實施起來都比較容易,而有些方法則不那么顯淺易懂。如果采用方法得當的話,上述方法可大幅提高系統整體性能。
我們不妨先來看看理想的 A/D 轉換器應該是什么樣的,了解哪些類型的誤差會阻礙我們獲得最佳性能。簡而言之,理想的 A/D 轉換器會為我們提供幾乎理想的數據。我說幾乎是理想的,是因為即便理想的 A/D 轉換器也存在量化誤差,但我們不妨以后再討論這一點。我們希望提高 A/D 轉換器的性能,所以我們不妨先來看看市場上分辨率最高的 A/D 轉換器,即 24 位 A/D 轉換器。
理想的 24 位 A/D 轉換器可提供 24 位可用數據。這種 A/D 轉換器可為給定輸入提供相同代碼或轉換結果的輸出,同樣也受到量化的限制。例如,如果我們對輸入范圍為 5.0V 的理想的 24 位 A/D 轉換器采用剛好 2.5V 的固定模擬信號,那么我們從 A/D 轉換器所得的唯一代碼就是8,388,608--標度值 (scale value) 的一半。如果我們對非理想轉換器采用相同電壓的話,那么輸出代碼不會固定為一半大小值,它實際上會給出不同的輸出,是否穩定并不確定,這是由轉換器的不理想特性造成的。不理想的 A/D 轉換器會造成量化誤差、偏移和增益誤差以及非線性。此外,噪聲和漂移也會導致測量誤差。
即便是理想的 A/D 轉換器也會發生量化誤差。量化誤差指數字化模擬輸入信號時產生的誤差。舉例來說,輸入范圍為 5V,那么每個代碼反映約 298 nV (5V/2^24) 的分辨率。如果我們開始時采用 0V 模擬輸入電壓,然后再逐步增加模擬輸入電壓,那么代碼會保持零不變,直至達到 149 nV 或 ? LSB 左右進行第一個代碼轉換。因此,即便采用理想的 A/D 轉換器,我們仍會遇到 +/- ? LSB 的量化誤差。之所以如此,是因為模擬輸入信號在 0V 到 149 nV 之間可取一個無限數值,但數字代碼只能為有限數值,理想情況下僅為 0。
我們常常一并考慮偏移誤差和增益誤差。偏移誤差是指對 A/D 轉換器采用零伏差動輸入時實際代碼與理想代碼之間的差異。增益誤差是指從負滿量程轉為正滿量程輸入時實際斜率與理想斜率之差。偏移和增益誤差通常是 A/D 轉換器中主要的誤差源。
非線性包括整數非線性 (INL) 和差動非線性 (DNL)。整數非線性指出的是輸出代碼與理想輸出之間差異的大小,而偏移和增益誤差已得到校正。在滿量程端點 (full-scale endpoint) 處取一理想線,一般來說,經測量得到的 INL 既為到這一理想線的最大偏差。差動非線性是指代碼值如何隨模擬輸入的變化而變化。就模擬輸入電壓的升高情況而言,代碼可能增加、不變或減少。根據模擬輸入增量的多少,代碼應該保持不變或者增加。如果出現這種情況的話,那么 ADC 就是單調性的。如果 ADC 跳過一個輸出代碼,那么此代碼稱之為缺失代碼。如果代碼輸出減少,那么我們就說 ADC 為非單調性。通過查看柱狀圖,我們可以得知是否存在缺失碼,以及關系代碼寬度的大小等。如果分配正常而無缺失碼,那么這就表明代碼寬度一致。
噪聲是隨時間變化的隨機輸出代碼,與偏移、增益和線性誤差無關。即便我們已經很好地校正了A/D 轉換器的所有其他誤差來源,我們仍會發現由于噪音的緣故出現輸出代碼變化。
漂移是指在給定輸入的情況下輸出代碼隨時間或溫度的變化而進行的變化。如果我們采用固定的模擬電壓,然后給設備加熱或去熱,輸出代碼就會隨著溫度而進行偏移。根據設備特性的不同,在給定的抽樣中漂移可能向相同方向發展,也可能呈隨機性。
盡管難以對所有誤差來源進行可視化,不過我們可通過芯片級設計技術或數據處理技術來解決這些誤差來源。在我們詳細了解如何補償誤差源之前,不妨先來了解一下A/D架構。在分辨率大于16位時,我們廣泛采用 Δ-Σ 架構。Δ-Σ 架構采用重復采樣技術來實現高分辨率數字輸出。圖 1 給出了簡化的 Δ-ΣA/D 轉換器結構圖。A/D 的主要組件是調制器和濾波器。調制器作為反饋環路環路工作,其目標是將差動信號誤差驅動為零。我們通過微差測量模擬輸入信號和反饋DAC信號來實現這一目的。Δ-Σ 架構中的Δ(delta) 因此得名。上述二者之差或信號誤差結合或合計到下一級。Δ-Σ 架構中的西格瑪由此而來。將總誤差與參照信號相比較,從而相應地設置比較器的輸出。如果誤差項為正值,則反饋 DAC 輸出升高,以嘗試減小差動誤差項。如果誤差項為負值,那么反饋DAC 輸出則降低,以嘗試減小差動誤差項。比較器 1 和 0 的密度與模擬輸入電壓成正比。
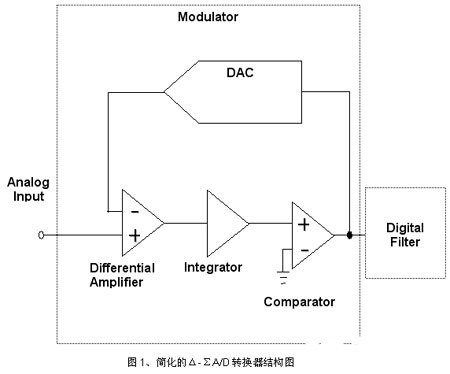
上述架構非常適用于高分辨率應用,因此我們不妨看看上述架構中各種類型的誤差源是如何暴露出來的。
我們可通過采用噪聲整形技術使Δ-Σ架構中的量化誤差達到最小。噪聲整形技術不會減小或消除量化噪聲;它只是將量化噪聲推向更高頻率、使之不再影響有關頻率(低頻)而已。因此,就量化噪聲而言,Δ-Σ架構的設計可以將量化噪聲的影響降至最低。
Δ-Σ架構中存在偏移和增益誤差,這與任何其他數據轉換器的情況一樣。此外,正是因為與任何其他數據轉換器的情況一樣,因而我們也可以通過簡單的校準技術將上述誤差最小化。為了進行偏移校準,我們采用 0V 或非常小的信號并讀取輸出代碼。如果結果為正,那么轉換器就存在正偏移誤差,我們從結果中減去偏移值;如果結果為負,那么轉換器就存在負偏移誤差,我們就向結果加上偏移值。
我們通過對A/D轉換器施加滿量程或近于滿量程的信號并測量輸出代碼來實現增益校準。偏移校準在增益校準之前進行。如果作圖顯示A/D轉換器的所有輸出代碼的話,我們看到增益誤差與理想輸出代碼斜率產生偏離,因此增益修正只不過是調整這條線的斜率而已。
INL存在于Δ-Σ架構中,就像任何其他數據轉換器一樣。但是,我們可以通過后處理數據對它進行補償。從理論上說,INL 可以逐個代碼地進行校準,但這是不實際的,因此通常我們選擇一些數據點來校正 INL。我們通過對表進行線性化來完成上述工作。
DNL通常對Δ-Σ架構而言不是問題。就其特性而言,反饋環路中1位DAC輸出是線性的,因此架構不調整也能獲得優異的DNL性能。
任何電子設備都存在噪聲,無法消除,但我們可以討論采用何種方法來減小這種誤差源。
任何電子設備都存在溫度漂移,無法消除,不過,如果可以預計漂移的話,那么我們就能通過線性化表來補償其影響。我們可通過溫度監測來實現上述目的。此外,我們還能很準確地確定漂移對系統性能的限制。
因此,總而言之:我們可通過噪聲整形技術來控制Δ-Σ架構中的量化誤差,通過校準來最小化偏移和增益誤差,采用線性化來改善 INL,而 DNL 則幾乎不存在,噪聲可最小化,而漂移則可糾正,其影響也可以估計。
最小化噪聲要比偏移和增益校準復雜一些。電子電路中有許多噪聲源:熱噪聲、1/f 閃爍噪聲和突發噪聲。在最小化噪聲方面,噪聲類型非常重要。熱噪聲從本質上說是高斯型的,因此我們可采用特定技術來最小化其影響。閃爍噪聲和突發噪聲從本質上說是非高斯型的,因此上述技術對處理這種噪聲源沒有效力。
我們在評估噪聲前,不妨先來看看噪聲與分辨率之間的關系。噪聲和分辨率相互關聯,彼此定義。噪聲可定義為輸出代碼與理想代碼間的隨機偏差。通常噪聲的表現形式是伏特、代碼、數量或PPM,而分辨率單位通常為位數或 dB。為了說明這一點,我們不妨假設理想的 24 位 A/D 轉換器具有5V模擬輸入范圍。顯然,分辨率為24位,因為這是理想情況。如果我們用 dB 來反映分辨率的話,那么分辨率就是6.02 * N dB(這里的 N 是位數),即 144.5 dB。我們通常稱這種定義為信噪比。如果我們用代碼來表示噪聲,那么噪聲就是一個代碼。如果我們用計數來表示噪聲,那么它就是 16,777,216 次計數。如果我們用伏特來表示噪聲,那么它就是 (1/16,777,216) * 5V,即 298 毫微伏。如果我們用 PPM 來表達噪聲,那么它就是 1/16,777,216 PPM,即 0.06 PPM。
這提出了另一個問題,非理想A/D轉換器的分辨率如何定義?“有效位數”(ENOB) 和/或“有效分辨率”等術語通常用于定義A/D轉換器的可用分辨率,如果考慮到設備的噪聲限制的話。為了有助于理解分辨率和“有效分辨率”或ENOB之間的區別,我們不妨先看一下理想的12位A/D轉換器。理想的12位A/D轉換器有4,096個代碼,也就是說分辨率為244 PPM。如果將模擬輸入轉換為數字值時我們強制給轉換器結果增加12位分辨率,那么我們就可以說我們獲得了24位分辨率的A/D轉換器。實際上只有12位有用。上面的例子可能并不像您想像的那么極端。例如,市場上實際銷售的A/D轉換器就號稱是24位A/D。在大約 25 Hz 的數據輸出速率時,其噪聲約 0.4 PPM,就其本身而言是相當不錯的。但是,0.4 PPM的噪聲意味著只有大約21.3位的有效分辨率。誰動了我們的24位分辨率?此外,如果您提高采樣率,那么噪聲可能會超過 600 PPM,這就使其甚至比 12 位 A/D 還糟糕!
有沒有可能實現真正的 24 位性能呢?答案是肯定的。不過我們要做好準備工作。幸運的是,我們可用各種技術來減小A/D轉換器的噪聲。此外,如果我們系統有干擾的話,那么我們也可采用類似的技術來減小或消除它。從本質上說,我們可使 A/D 轉換器獲得更高的實際分辨率位數,從而實現更高的整體系統性能。這就是綜合各種技術的優勢所在。
為了實現更高性能,我們必須了解 A/D 轉換器功能有多強。一項確定 A/D 轉換器性能的廣為采納的技術就是進行柱狀圖分析。柱狀圖可清楚地告訴我們A/D轉換器在DNL、DC偏移和噪聲方面的情況。柱狀圖顯示了輸出代碼和輸出代碼出現次數之間的對比情況。從柱狀圖測試中,我們可評估出代碼寬度或容量大小 (DNL)。通過將輸入接地,我們可能評估出噪聲方面的信息。如果A/D轉換器DNL較好,噪聲為白噪聲,那么柱狀圖就應類似于高斯型或正常分布。如果代碼寬度小,那么代碼出現的就少;如果代碼寬度較大,那么代碼出現就較多。如果代碼不出現,那么就表明代碼缺失。柱狀圖分析能夠成為一種非常強大的工具。我們可方便地了解 DNL 性能和噪聲特性。
如果柱狀圖顯示 DNL 性能較好,分布也正常,那么我們就可假定噪聲為白噪聲。由于我們觀察的是Δ-ΣA/D 轉換器,因此從定義而言差動非線性應足夠。ADS1252 Δ-Σ A/D 轉換器的數據采樣柱狀圖為 32,768,這表明 DNL 性能近于理想情況,而輸出代碼分布與正常分布很類似。因此,我們可以假定該 A/D 轉換器的噪聲為白噪聲。這意味著我們可使用統計學方法來評估噪聲。
如前所述,如果A/D轉換器數據有一般的特性模式,那么我們可將數據集放入一般模式中。一般模式通常是指概率分布。由于數據表現出白噪聲特性,因此我們可用高斯機率密度函數來評估噪聲。函數顯示了信號超出特定值的可能性,如以下方程所示:

這里:
u =真實平均數
x =信號值
s =標準偏差
從該方程式可看到,隨著 x 從平均值移開,可能性降低,而輸入信號會超過給定值。使用該方程式,我們可實際計算信號在給定時間內處于特定范圍的可能性。
因此,我們可采用高斯幾率密度函數作為數據模型。下一個問題就是我們的模型到底有多好?我們用兩種標準統計原理來解決這一問題。首先,平均法則指出,如果總體存在一個真實的平均數 (u)且x為總體中n個個體隨機采樣的采樣平均數,那么隨著n不斷加大,采樣平均數 (x) 也會越來越接近真實平均數 (u)。由于我們討論的是白噪聲的情況,因此采樣平均數會與真實平均數很接近,前提是采樣規模足夠大。因此,我們知道我們可以信任計算得出的真實平均數 (u),因為它與真實平均數 (u) 有關。
我們如何了解標準偏差計算得到底好不好?我們可用中心極限定理來回答這一問題。該定理指出,如果總體具有真實平均數 (u) 和真實標準偏差 (s),那么總體中n個個體所有可能的采樣平均數集合的概率分布就會隨n的增大越來越接近平均數 (u) 和標準偏差 (s/sqrt n) 的正常分布。從根本上說,如果我們采樣更多的話,那么我們就能減小標準偏差。
如果我們完全依賴中心極限定理,那么我們可采用越來越多的采樣,從而使標準偏差越來越小。不過改善的速度不會太快。采樣數量增加實現標準偏差改善也有一個限制。一旦采樣數超過了這個限制,那么您就不會再得到任何好處,甚至還會增加標準偏差。采樣數量有限制的理論建立在方差的基礎之上。方差理論廣泛用于評估信號源的頻率穩定性,不過它適用于任何采樣系統。換言之,系統穩定時采樣只會降低標準偏差。穩定性受許多因素影響,包括隨即事件,甚至系統中的漂移。
對于主要包括白噪聲的系統而言(與我們這里討論的系統類似),平均方差是標準方差的測量方法。在這種類型的系統中,我們可采用方差來預計標準方差。通過使用方差,我們可實際預計采樣對系統的影響。從根本上說,方差分析之所以起作用,是因為我們收集了大量采樣并分析采樣數量上升時方差如何變化。方差最小時的采樣數量就是我們給定系統的最佳采樣數量。這是一個非常有用的工具,有助于我們快速而方便地優化采樣技術,從而獲得最大的系統性能。
我們不妨將理論運用到實際的 24 位 A/D 轉換器來進行檢測。我們前面提到的 24 位 A/D 轉換器在25 Hz 采樣率上噪聲約為 0.4 PPM。將 PPM 轉化為位數,我們可評估應當如何對 A/D 轉換器進行采樣以獲得期望的性能。在 PPM 和位數之間相互轉化的方程式如下所示。

在 PPM 與位數之間相互轉化的方程式
應用以上方程式時,為了獲得 24 位分辯率,我們需要將噪聲降低至 0.06 PPM。這就是說,我們必須使噪聲減少幾乎 7 個值才可以。根據中心極限定理,我們需要采用約 49 個采樣來實現上述噪聲性能。不幸的是,這會讓我們的采樣率降至約 0.4 Hz,而我們的信號帶寬(-3dB 頻率)則降至約0.1 Hz。這種采樣率不僅對于許多應用而言太慢了,而且信號帶寬也會對性能造成災難性影響,因為輸入信號的任何變化都會對建立時間造成極大影響。我們能夠以更快的采樣速率運行 24 位 A/D,但有效分辯率的降低造成的問題比信號速率還嚴重,因此我們追求高速度反而會使問題惡化。
幸運的是,我們可以找到解決該問題的方法。ADS1252是一種采樣頻率為 40 kHz 的 24 位 Δ-Σ A/D轉換器。如果有效分辯率在 40 kHz 速率上足夠高,那么我們就可獲得足夠的分辯率,能夠對數據進行采樣以提高分辯率,并仍然可獲得足夠的采樣率。我們不妨來看看 ADS1252 的規范性能,其在 41,667 Hz 數據速率上的噪聲為2.5 PPM。根據中心極限定理,我們應采用 1,736 個采樣來實現 0.06 PPM 的噪聲,這時的數據速率為 24 Hz。從論文上看,我們已獲得了解決方案。此外,由于我們的 A/D 運行時采用更快的采樣率,從平均采樣數來看,總濾波器衰減較慢。這意味著我們可獲得更高的信號帶寬。例如,我們早先談到了帶有 sinc3 濾波器的 25 Hz 的 24 位 A/D 轉換器,其輸出的信號帶寬約為 6 Hz。采用平均數據的 ADS1252 的信號帶寬約為 10 Hz,因此我們實際上提高了信號帶寬。
為了弄明白該解決方案是否切實可行,我們收集了數以萬計的采樣,并采用平均和方差技術來檢查是否確有效果。表 1 和表 2 給出了不同理論的噪聲和分辯率比較。


表中數據顯示了一些有趣的結果。方差分析與實驗數據穩和很好;但是,實驗數據與中心極限定理預計應得的結果則存在一定偏差。這很可能是由于系統干擾造成的。進一步分析方差顯示,采樣大于 12,000 沒有任何好處。對超過 12,000 次的采樣進行平均,實際上反而會降低噪聲性能,因為系統因漂移而造成不穩定。因此,我們采用本方法可對系統性能進行優化。
責任編輯:gt
 電子發燒友App
電子發燒友App





















評論