淺談嵌入式中ADC技術

[導讀] ?生活環境周圍信號萬萬千，對于一個嵌入式er。我們利用技術去了解世界、改變世界。而一個產品要與外界物理環境打交道，一個至關重要的觸角就是采樣真實模擬世界的信號，翻譯成芯片可理解的數字信號，進而實現很多為人服務的應用產品。那么提到采樣，ADC技術你繞不開，今天總結分享一下ADC的點點滴滴。

啥是ADC

在現代電子工業技術中，模數轉換器(ADC, A/D，或A-to-D)是一種將模擬信號轉換成數字信號的系統。ADC還可以提供隔離的測量，例如將輸入模擬電壓或電流轉換為表示電壓或電流大小的數字的電子設備。通常情況下，數字輸出是一個與輸入成比例的二進制補碼，但也有其他的可能性。舉些栗子：

KTV中麥克風將你唱歌的聲音轉成數字音頻信號，經由信號處理，功放再播放出來

數碼相機將物體表面反射的光線轉換為數字信號，從而成像

疫情期間必用物資額溫槍，將人體紅外輻射經由光電轉換成電壓，最終轉換為數字信號進行溫度顯示

.......舉不勝舉。

ADC將連續時間和連續幅度的模擬信號轉換為離散時間和離散幅度的數字信號。轉換涉及輸入的量化，因此必然會引入少量的誤差或噪聲。此外，ADC不會連續執行轉換，而是定期進行轉換，對輸入進行采樣，從而限制了輸入信號的允許帶寬。

ADC的性能主要由其帶寬和信噪比（SNR）來表征。

ADC帶寬?(Band width)：ADC的帶寬主要由其采樣率來表征。

ADC的SNR：SNR(signal noise ratio)是指信噪比，受許多因素影響，包括分辨率，線性度和準確性（量化級別與真實模擬信號的匹配程度），混疊和抖動。ADC的SNR通常以其有效位數（ effective number of bits：ENOB），它返回的每個度量的位數平均來表示，而不是噪聲。理想的ADC的ENOB等于其分辨率。

故，選擇ADC以匹配待數字化信號的帶寬和所需的SNR。如果ADC的采樣率大于信號帶寬的兩倍，那么根據Nyquist–Shannon采樣定理，就可以實現完美的重構。量化誤差的存在甚至限制了理想ADC的SNR。但是，如果ADC的SNR超過輸入信號的SNR，則其影響可能會被忽略，從而導致模擬輸入信號的本質上是完美的數字表示。

整這么多文字還是不直觀易懂，到底啥是ADC，來個會動的圖吧：

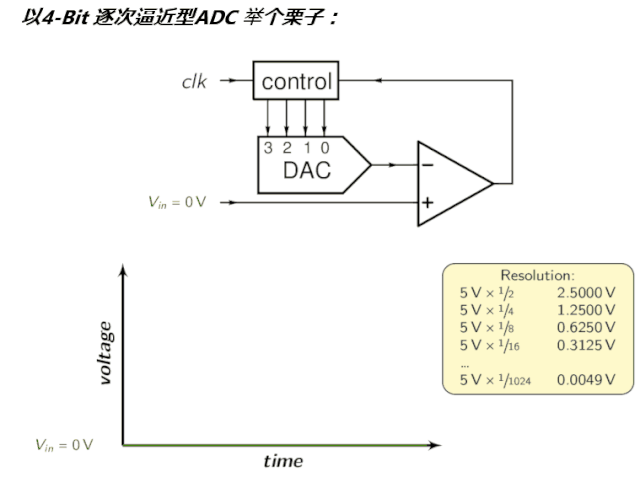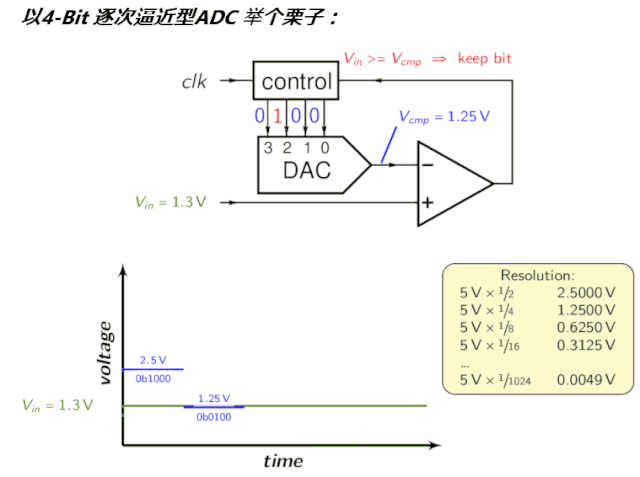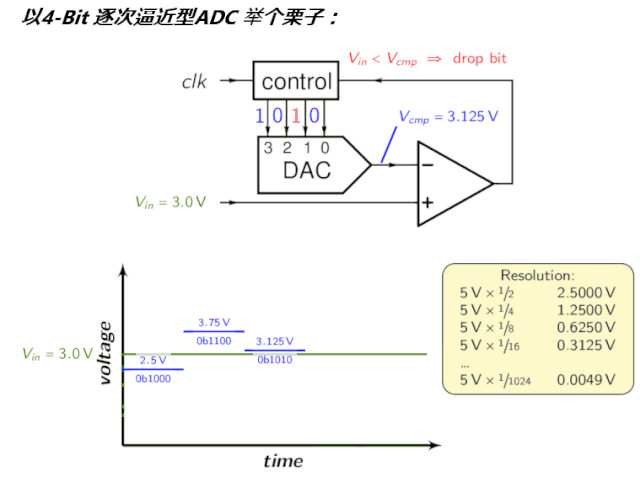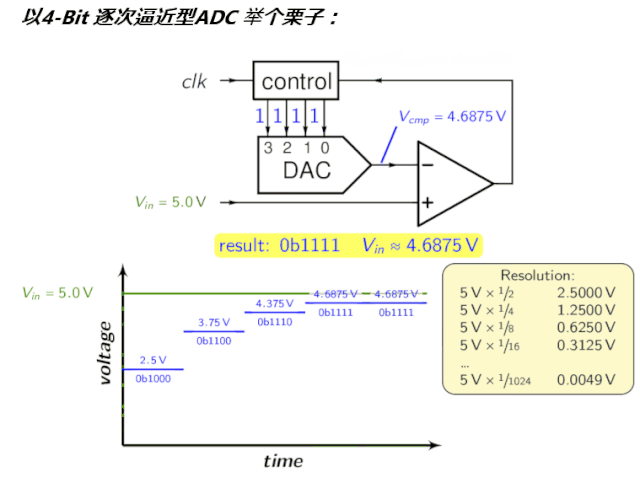
須理解的指標

分辨率

ADC看成一個黑匣子，基本的有一個模擬輸入及其等效數字輸出。下圖所示示例為一個N位ADC。N通常是6到24之間的任何值，常見的是8、10、12或16位。參考電壓可能為單端電壓，也可能為一個~,是一個正負電壓參考源。

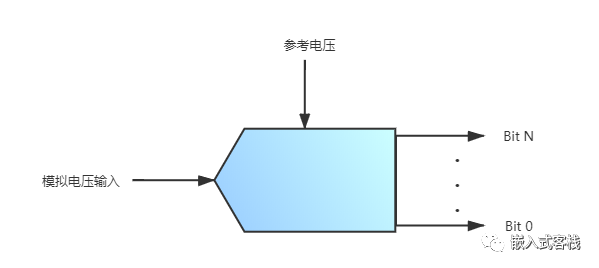
輸入是一個模擬電壓，范圍從0到參考電壓，參考電壓取決于實際ADC及外圍電路。?假設使用N位，則可能有個可能的數字輸出值，則1位表示的值為。在很多書上也稱這個指標為LSB（Least Significant Bit）。

這便是分辨率的概念。模數轉換器的分辨率表示在模擬值范圍內它可以產生的離散值的數量。該分辨率決定了量化誤差的大小，因此決定了不使用過采樣的理想ADC的最大平均信噪比。

舉個栗子，如果給定ADC的最大輸入值為5.0V，而ADC為10位類型，則每一位表示。這個ADC的分辨率，或者說量化步長，是4.89 mV。這是它的絕對理論分辨率。在這種特殊情況下，信號的分辨率不能高于。這個極限稱為量化誤差，所有的ADC，即使是完美的ADC，都有一定程度的量化誤差，具體取決于ADC的分辨率。分辨率的數學定義為：

其中及為ADC的參考電壓，M為ADC的量化位數。可見M越大，Q數值越小，分辨率越高。

這個公式簡單解讀：就是將參考電壓按照進行等分，比如10位ADC，就是將參考電壓等分成1024份，輸入電壓與參考電壓之比乘以1024，即為ADC的值。故

量化誤差

量化誤差是由理想ADC中的量化過程產生的。由于ADC的模擬輸入電壓與輸出數字化值之間的存在舍入誤差。?在理想的ADC中，量化誤差均勻地分布在和之間，并且信號具有覆蓋所有量化水平的均勻分布，因此信號量化噪聲比SQNR（Signal-to-quantization-noise ratio）定義為：

其中,M為ADC的位數，M位數越大或越高，SQNR也越大。

精度

量化誤差和非線性是模數轉換器所固有的誤差指標。用最低有效位（LSB）的單位進行度量。比如一個10位ADC，LSB為。

非線性度

實際使用的ADC除了上面說的量化誤差外，還具有更多的誤差源：

差分非線性誤差DNL(Differential Non-Linearity):當ADC輸出在應該改變的時候沒有改變，就會出現DNL誤差。例如，假設給定輸入的當前輸出代碼是01101100，并且輸入值增加了半步量化。代碼應該是01101100 + 1位，或者01101101。當輸入電壓低于當前輸入電壓時，也會發生相反的情況。此時由于種種原因，這種情況可能不會發生。在本例中，ADC的誤差為±1位DNL。

積分非線性誤差INL(Integral Non-Linearity)：如果量化水平在整個輸入范圍內分布不均勻，就會出現INL誤差。例如，某ADC具有12位(4096個計數)分辨率和4.096V的參考電壓。每個比特數正好表示輸入電壓變化的1.000mV，因此，輸入電壓為4096 mV，輸出電壓為1111 1111 1111，即0xFFF。對于某些adc，輸入4095mV，甚至4094mV，仍然會得到0xFFF的數字輸出。實際情況是，在整個輸入范圍內，1位的值發生了非常微小的變化，比如1.001mV或0.999mV。積累的誤差會導致一個或兩個比特精度的全量程誤差。

在為特定應用指定ADC時必須考慮這些因素。

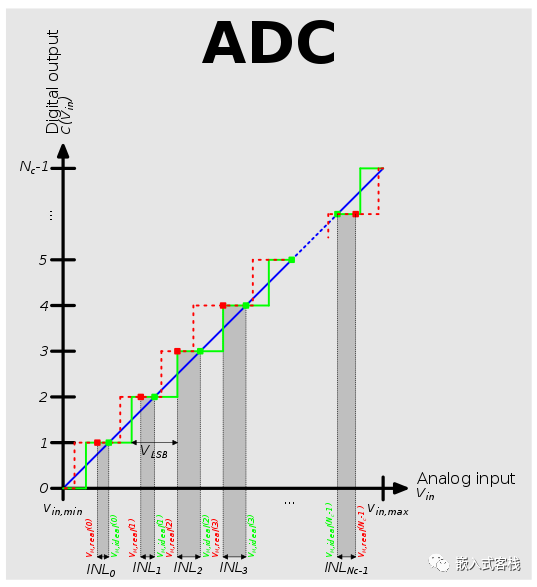
所有ADC都存在由其物理缺陷引起的非線性誤差，導致其輸出偏離其輸入的線性函數(或其他函數，在故意使用非線性ADC的情況下)。這些誤差有時可以通過校準來減輕，或通過測試來避免。所謂校準，比如可以通過量點線性校準，假定y為ADC數值，x為輸入模擬電壓:

其中：

應用實施策略:將上述k/b，利用兩個點進行校準，將校準數據k/b存儲在非易失存儲器中。補充說一下：工程實踐中需要校準的原因還因為選取的外圍電阻、電容器件都有誤差，所以這也是另一個需要標定的重要原因。

采樣率

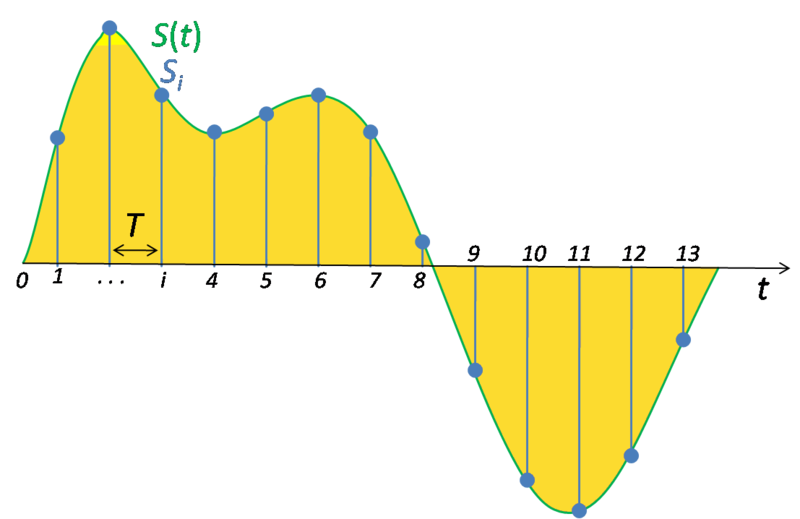
模擬信號在時間上是連續的，因此有必要將其轉換為數字序列，這是數字信號處理的基礎。因此，需要定義從模擬信號中采樣數字序列的速率。該速率稱為轉換器的采樣率或采樣頻率。可以采樣連續變化的帶限信號，然后可以通過重構濾波器從離散時間值中再現原始信號。奈奎斯特-香農采樣定理表明，只有當采樣率高于信號最高頻率的兩倍時，才可以忠實再現原始信號。個人在使用時，一般會選4倍以上。

由于實際的ADC不能進行瞬時轉換，因此在轉換器執行轉換期間(稱為轉換時間)輸入值必須保持恒定。一個被稱為采樣保持電路——在大多數情況下，它使用一個電容來存儲輸入端的模擬電壓，并使用一個電子開關或柵極來斷開電容與輸入端的連接。許多ADC集成電路包括內部的采樣保持電路模塊。圖中的T為采樣周期，其倒數就是采樣頻率。

混疊

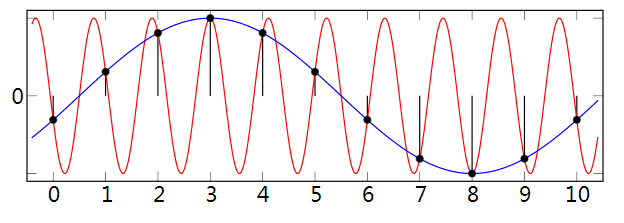
ADC通過在不連續時間間隔（離散的含義）內對輸入值進行采樣來工作。假設以高于奈奎斯特速率的頻率對輸入進行采樣（定義為有用信號頻率的兩倍），則可以重構信號中的所有頻率。如果對高于奈奎斯特速率一半的頻率進行采樣，則會將它們錯誤地檢測為較低頻率，這一過程稱為混疊。之所以會出現混淆，是因為每個周期對函數進行兩次或兩次以下的瞬時采樣會導致丟失周期，從而出現頻率錯誤地降低的情況。例如，以1.5 kHz采樣的2 kHz正弦波將重構為500 Hz正弦波。

為了避免混疊，ADC的輸入必須經過硬件低通濾波，最簡單的實現形式為一階無源RC濾波網絡，以去除采樣率一半以上的頻率。這種濾波器被稱為抗混疊濾波器，它對于實際的ADC系統至關重要，該系統適用于具有更高頻率內容的模擬信號。在需要防止混疊的應用程序中，可以使用過采樣來大大減少甚至消除混疊。

例如：六種不同采樣速率采集的數字序列重建的4種波形。其中兩種波形在采樣率足夠情況下未出現混疊。另外兩個說明了在較低速率下會失真（混疊增加）。

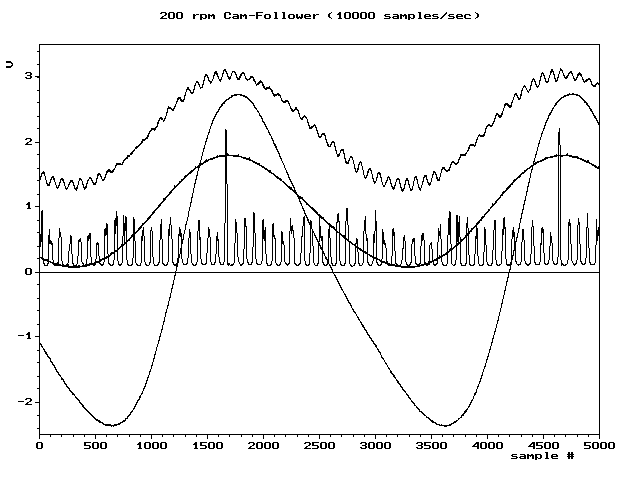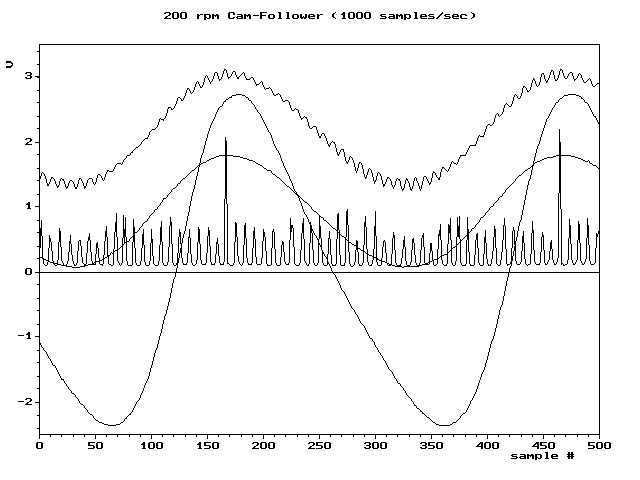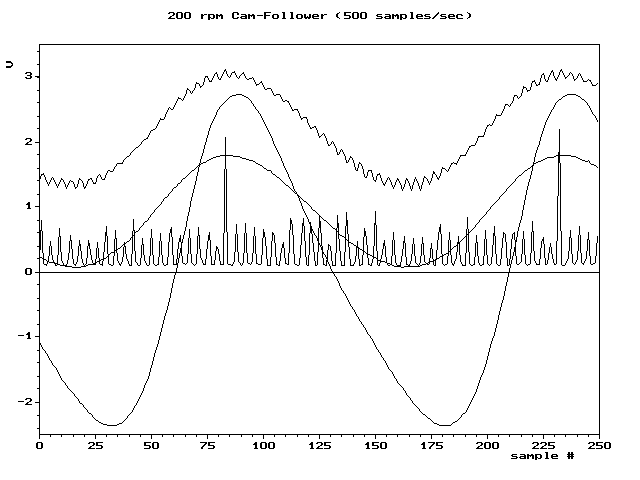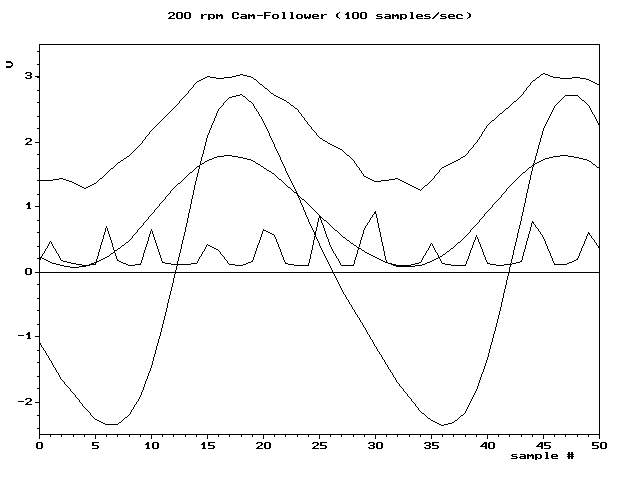
過采樣

為了經濟起見，通常以所需的最小速率對信號進行采樣，結果是引入的量化誤差是白噪聲在轉換器整個通帶上的擴散。如果以遠高于奈奎斯特速率的速率采樣信號，然后進行數字濾波以將其限制為信號帶寬，則會產生以下優點：

過采樣可以更輕松地實現模擬抗混疊濾波器

降低的噪聲，尤其是在過采樣之外還采用噪聲整形處理后。

白噪聲長啥樣？

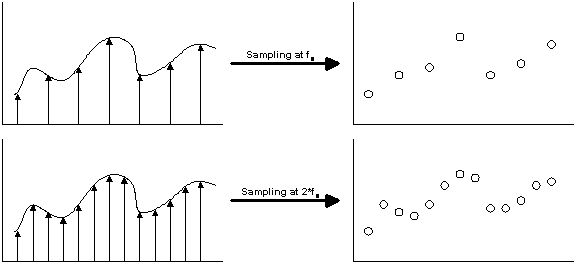
過采樣通常用于音頻ADC中，與典型晶體管電路的時鐘速度（> 1 MHz）相比，所需的采樣率（通常為44.1或48 kHz）非常低。在這種情況下，可以以很少的成本或不增加成本就可以大大提高ADC的性能。此外，由于任何混疊信號通常也都在頻帶外，因此使用非常低成本的濾波器通常可以完全消除混疊。下圖比較直觀，可以看出提高采樣頻率，可以更為真實的重建原始信號，而采樣頻率低些，對于信號的細部則無法準確重建。