電源設備可靠性的研討
本文所研討的可靠性問題,適用于幾乎所有的電子系統和機電一體化設備。電源設備尤其是交流電源設備,作為電子系統的基礎部件,長期、穩定地保持正常工作能力尤為重要。美國貝爾實驗室的研究報告指出:造成計算機等精密電子設備損壞的主要原因是電壓的浪涌(surge),即短期(10ms左右)或長期的過電壓,占全部損壞原因的45.3%。雷擊占9.4%。引起設備工作不正常和誤碼的主要原因是電壓過低(含短期脈動)(sags)占87%,以及脈沖尖峰干擾占9%。因而,世界上許多著名的制造商均有嚴格的場地供電標準,責成用戶予以保證。
近年來,電源設備日趨復雜,元器件的品種和數量增加很快;使用環境也變得惡劣多樣;而所服務的電子系統又越來越重要和昂貴。以交流參數穩壓電源為例,已廣泛地應用于車載、艦載、地面的軍用裝備,航空航天部門,鐵路和交通的信號和通信系統等方面。電源需要日夜不停地連續運行,還要經受高、低溫,高濕,沖擊等考驗。運行中往往不允許檢修,或只能從事簡單的維護。這一切就使得電源設備的可靠性研究,變得刻不容緩,十分重要了。其實,早在上世紀70年代,英國電氣工程師學會發表的論文就指出:在提供軍事通信的英國天網系統的設計研制中,中心課題首先是可靠性!
國際上,通用的可靠性定義為:在規定環境條件下,和規定的時間內,完成規定功能的能力。此定義適用于一個系統,也適用于一臺設備或一個單元。由于故障出現的隨機性質,用數學方式來描述可靠性,常用“概率”來表示。
從而,引出可靠度[R(t)]的定義:系統在規定環境條件下和規定時間內,完成規定功能的概率。
例如:對N個產品進行試驗,每經過Δt的時間間隔檢查一次,每次出故障的產品數為ni,則在T時間內的可靠度R(t)為:R(t)=[(N-)/N],可近似為:
R(t)=(N-)/N
R(t)的數值范圍為:0≤R(t)≤1。R(t)的值越接近于1,則表示可靠性越高。如系統有N個單元組成(串聯方式),各單元的R(t)分別為R1(t),R2(t)……RN(t),則整個系統的RΣ(t)=R1(t)·R2(t)…RN(t)。可見,系統越復雜,可靠性越差。
1影響系統可靠性的因素
涉及系統可靠性的因素很多。目前,人們認識上的主要誤區是把可靠性完全(或基本上)歸結于元器件的可靠性和制造裝配的工藝;忽略了系統設計對于可靠性的決定性的作用。據美國海軍電子實驗室的統計,整機出現故障的原因和各自所占的百分比如表1所列:
lim
Δt→0
N→∞
表1整機故障原因統計
| 故障原因 | 占總失效數的(%) |
|---|---|
| 設計上的原因元器件質量上的原因操作和維護上的原因制造上的原因 | 40302010 |
2衡量系統可靠性的指標及其數學關系
2?1失效率λ
λ定義為:該種產品在單位時間內的故障數。即:
λ=dn/dt
相對于每一個依然正常工作的樣品的失效率,
λ=(1/NS)·dn/dt
式中:NS為總試驗品N,經過Δt時間以后,依然正常工作的樣品數。
工程上,采用近似式。如果在一定時間間隔(t1-t2)內,試驗開始時的正常工作的樣品數為ns個,而經過(t1-t2)后出現的故障樣品數為n個,則這一批樣品中對于每一個正常樣品的失效率λ為:
λ=n/[ns(t1-t2)]
失效率λ的數值越小,則表示可靠性越高。λ可以作為電子系統和整機的可靠性特征量,更經常作為元器件和接點等的可靠性特征量。其量綱為[1/h]。國際上常用[1/109h]稱為[fit],作為λ的量綱。
例如,美國GE公司97F8000系列用于交流電源的金屬化薄膜電容器的工作壽命為:100只電容器在工作60000h以后,95只電容器正常,5只電容器此期間有可能出現故障。則:
λ=n/〔ns(t1-t2)〕
代入ns=100,n=5,(t1-t2)=60000h,則有:
λ=0.83·10-6/h=830[fit]。
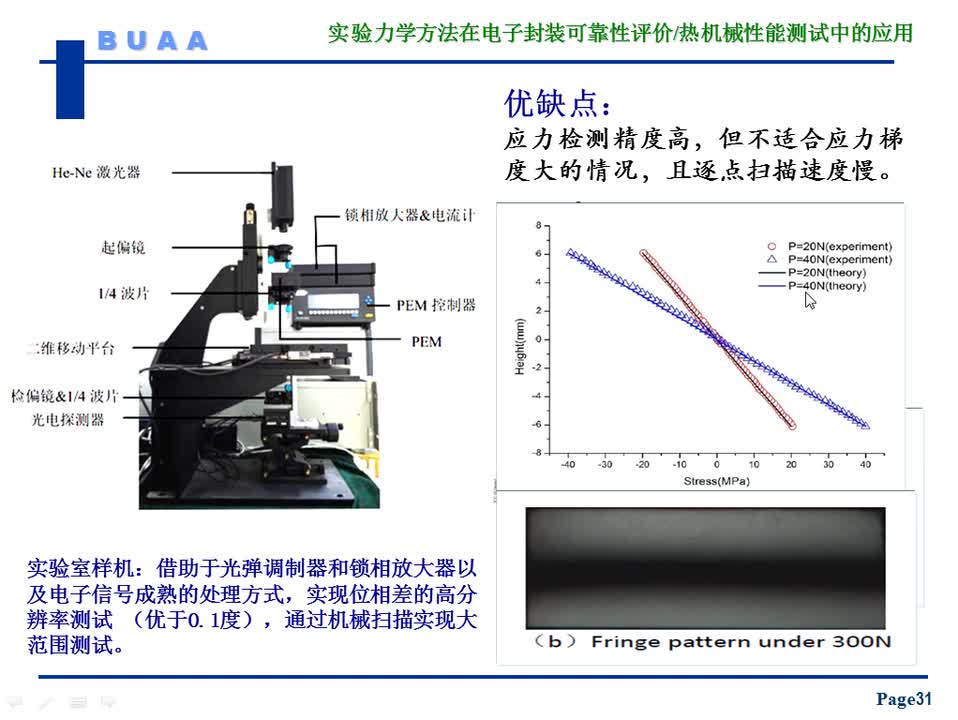
美國1974年頒布的標準工作條件下的元器件基本失效率如表2所列(供參考)。
2?2平均無故障工作時間MTBF
MTBF的定義為:電子系統無故障工作時間的平均值。
對于一批(N臺)電子系統而言:MTBF=ti/N[h]
式中:ti—第i個電子系統的無故障工作時間[h];
N—電子系統的數量。
工程上,如一臺整機,在試驗時,總的試驗時間為T,而出現了n次故障。出現故障進行修復,然后再進行試驗(維修的時間不包括在總試驗時間T內)。則:
MTBF=T/n[h]
MTBF數值越大,則表示該電子系統可靠性越高。MTBF的參考數據如表3所列:
表3MTBF的參考數據
| 電子系統名稱 | MTBF/(h) |
|---|---|
| 1978年集成彩色電視接收機(國際水平) | ≥2000 |
| 阿波羅宇宙飛船電子計算機 | (2~2.5)×104 |
| 英國天網衛星系統 | 1000 |
| 美國“泰康”遠程導航設備(20世紀80年代) | 150 |
| Simods數字頻率合成器 | 10×104 |
T=60000h,100只受試電容共出現5只有故障,那么對于每只電容器來講:
MTBF=100T/n=120×104h。
在此,必須明確不論是失效率λ,還是平均無故障工作時間MTBF,均為衡量設備或元器件可靠性的“概率”性的指標。切不可誤解為對于上述電容器每只可以工作120萬h以后才會出現故障。具體到某一只電容器,也可能一用就壞,更大的可能是工作60000h以后還是很正常。
2?3平均維修時間MTTR
MTTR的定義為:系統維修過程中,每次修復時間的平均值。即:
表2美國1974年頒布的標準工作條件下元器件失效率
| 元器件類型 | λ(fit) | |
|---|---|---|
| 電阻器 | 固定薄膜 | 4 |
| 合成電位器 | 138 | |
| 線繞電位器 | 167 | |
| 電容器 | 紙介 | 70 |
| 鋁電介 | 117 | |
| 可變陶瓷 | 393 | |
| 繼電器 | 6 | |
| 半導體二極管 | 硅 | 20 |
| 齊納 | 18 | |
| 半導體三極管 | 鍺PNP | 56 |
| 鍺NPN | 140 | |
| 硅PNP | 63 | |
| 硅NPN | 33 | |
表4國際通信衛星系統有關R(t)參考數據
| 電子系統名稱 | R(t)/(%) | |
|---|---|---|
| 國際通信衛星Ⅲ號 | 地面站 | 99.7 |
| 天線 | 93.5 | |
| 電源 | 94.2 | |
| 國際通信衛星Ⅳ號轉發器電子設備 | 連續工作2個月時 | 99.9 |
| 連續工作7年后 | 79.0 | |
| 供電系統國際水平 | 99.95 | |
式中:Δti—第i次的修復時間[h]。
M—修復次數。
任何設備無論如何可靠,永遠存在著維修的問題。所以MTTR總是越小越好。因而,實現方便快捷的維修或不停機維修有著重大的價值。
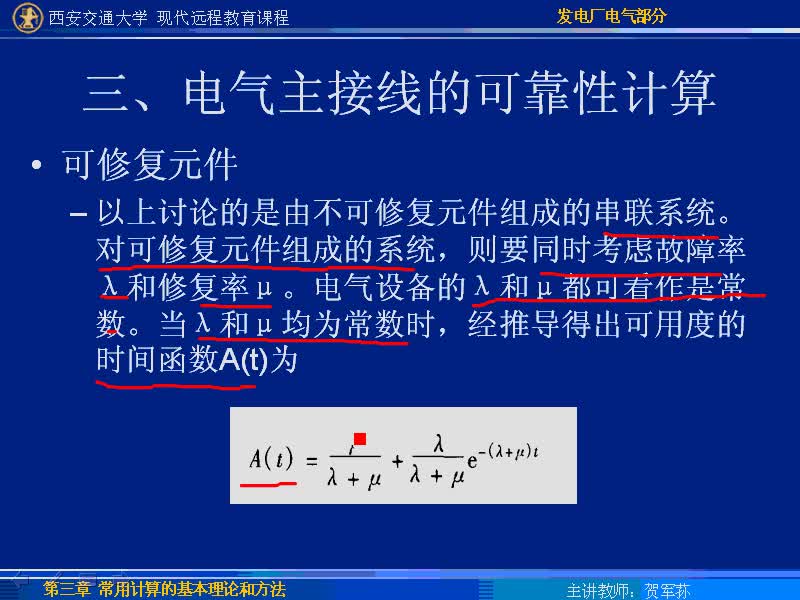
2?4有效度(可用度)A
A的定義為:電子系統使用過程中(尤其在不間斷連續使用條件下)可以正常使用的時間和總時間的比例(通常以百分比來表示)。即:
A=MTBF/(MTBF+MTTR)
A值越接近于100%,表示電子系統有效工作的程度越高。
實際上,設備MTBF受到系統復雜程度,成本等多方面因素的限制,不易達到很高的數值。盡量縮短MTTR也同樣可以達到增加A的目的。對于高失效率單元,采用快速由備份單元代替失效單元的冗余式設計,可以在MTBF不很高的情況,使MTTR接近于0,這樣,也可以使A近于100%。
2?5可靠度R(t)
可靠度R(t)是衡量電子系統可靠性的最基本的指標。可從可靠度R(t)的定義中導出故障概率F(t)。即:
F(t)=1-R(t),或R(t)=1-F(t)。
可以看出,對于R(t)和F(t)來講,其值均為時間量t的函數。極端來講,t=0時,任何系統的R(t)=1,〔F(t)=0〕。在t=∞時,任何系統的R(t)=0,〔F(t)=1〕。R(t)和F(t)只有在指定的時間范圍以內才有具體的意義。在實際使用中常用年可靠度P來表示。
年可靠度P的定義為:電子系統在規定的環境條件下,在1年的時間內,完成規定功能的概率。例如P=0.9,就說明系統在一年內有90%的可能不出現故障。(也即有10%的可能會出現故障)。如果在一個地點有10臺同類設備,則平均1年會有1臺設備可能需要進行維修。
國際通信衛星系統有關可靠度R(t)的參考數據如表4所列。
2.6失效率λ,平均無故障工作時間MTBF和可靠度R(t),故障概率F(t)之間的數學關系
依據λ,MTBF,R(t),F(t)的定義和基本數學表達式,經數學運算以后,可得出以下的相互數學關系(運算過程從略)。
(1)MTBF=1/λ或λ=1/MTBF,
即λ和MTBF互為倒數關系。
(2)R(t)=e-λt或R(t)=e-t/MTBF=1/et/MTBF,
即R(t)和λ之間為指數關系。
(3)F(t)=1-R(t)或R(t)=1-F(t),
這樣,λ,MTBF,R(t)三個指標,可以通過上述換算,從一個量算出另兩個量的對應數值。在不同的場合,以上三個指標都可能在衡量電子系統可靠性時交替使用。
3提高系統可靠性的途徑
3?1認真從事系統可靠性的設計
電子系統的可靠性模型,大體上有以下三種形式:
(1)串聯系統的可靠性模型
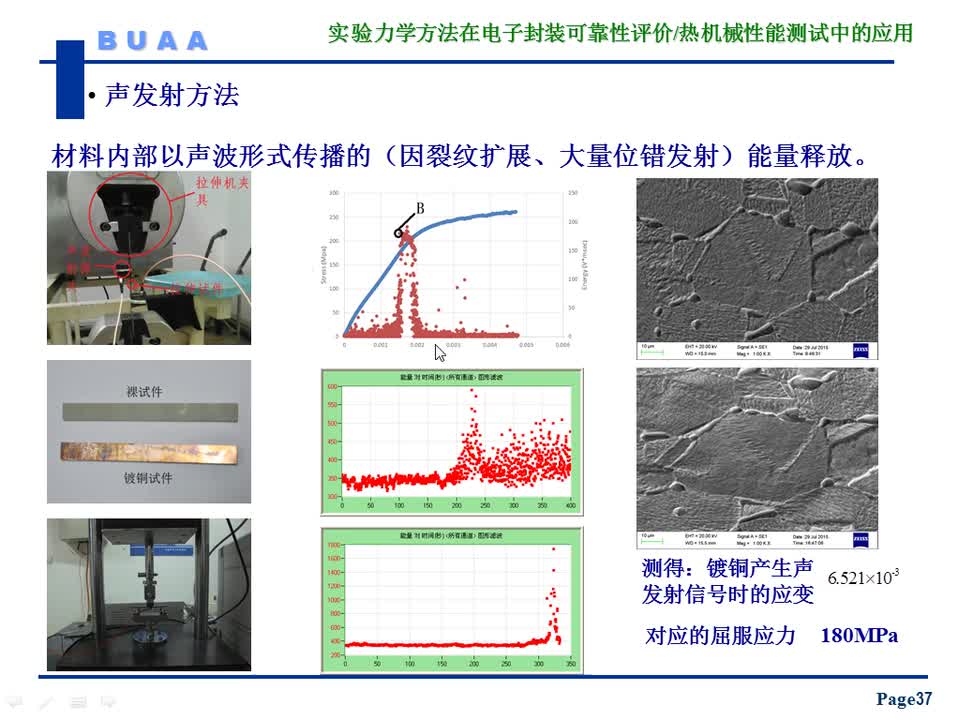
串聯系統模型如圖1所示。串聯系統是指它的每一個元件對于系統的正常工作都是必須的,不可或缺的;任何一個元件的失效,將導致系統工作不正常。這是一種較常見和簡單的系統。
如果系統有N種元件,每種元件的失效率為λi(i=1~N),則串聯系統的總失效率:
λ?=n1λ1+n2λ2+……nNλN
總的無故障工作時間:
MTBF?=1/λ?=1/[n1λ1+n2λ2+……nNλN]
年可靠度:P=1/e8760·λ?=1/e8760/MTBFN。(因每年共8760h)。
例(1):優質的交流參數穩壓電源單元的MTBF0=20萬h,如果每臺鐵路信號屏用10只電源單元。則每屏交流電源部分的MTBF=MTBF0/10=2萬h。相當于年可靠度P=0.645=64.5%。即年故障概率F=1-P=35.5%。也就是每臺電源屏每年有35.5%的可能性需要維修。如果一個車站有10臺信號屏,則每年有3~4臺交流參數穩壓電源單元有可能出故障,就是很正常的情況。這也和某部門有100臺電源單元,大都連續工作的故障概率相仿。
![]()
圖1串聯系統模型
可見,雖然每單元交流參數穩壓電源MTBF0=20萬h,已經比其他類型的交流電源高了許多倍(其它類型電源MTBF往往只有數千h)。但處于連續工作條件下的串聯系統模型的信號屏的可靠度并不十分令人滿意。
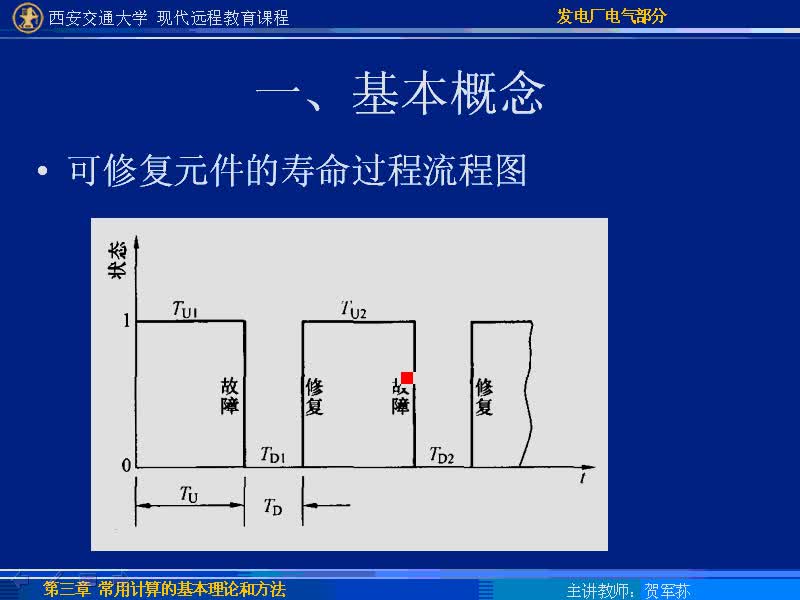
(2)并聯系統的可靠性模型
并聯系統模型如圖2所示。圖中:U1,U2均可單獨地實現系統的功能,而且U1,U2任何一個單元出現故障,將自動(或手動)和輸入、輸出端斷開,同時接入另一個互為備份的單元。
顯然,并聯系統的任何一個單元的失效,均不會影響系統的功能,只有在二個單元均失效時,系統才不能正常工作。同理也可以N個單元并聯構成一個系統。
其數學關系為:
故障概率:F(t)=F1(t)·F2(t)…FN(t)
若F1(t)=F2(t)…=FN(t)則可靠度:
R(t)=1-F(t)=1-[F1(t)]n
例(2):優質的交流參數穩壓電源單元的MTBF0=20萬h,每臺鐵路信號屏用10只電源單元。若每個電源單元有2臺互為備份的電源構成并聯系統。則每臺電源的年可靠度:
P1=1/e8760/MTBF,P1=0.957
年故障概率F1=1-P1=0.043
所以,每個電源單元(2臺互為備份的電源構成)的年故障率為:
F11=[F1]2=1.85×·10-3
每個電源單元的年可靠度:
P11=1-F11=1-[1-P1]2
=1-1.85×10-3=0.998=99.8%
每臺鐵路信號屏有10只電源單元,則每臺信號屏的年可靠度:
P=(P11)10
=(0.998)10=0.98=98%,
即年故障概率F=1-P,為2%。
若一個車站有10臺信號屏,則每年只有2%的可能性,會進行一次維修。與例(1)串聯系統相比,故障概率降低了近18倍。
結論很明確,在每個單元的可靠性受各種限制不可能太高,而又要求系統具有很高的可靠度的情況下,采用并聯系統代替串聯系統是提高電子系統可靠性的根本方法。美國波音707飛機的發電機采用4臺并聯系統(用1備3),核電站的直流供電采用三臺并聯系統(用1備2),都是很好的例子。
并聯系統的成本將高于串聯系統,但為了保證必要的可靠性,花些代價是必須的也是值得的。
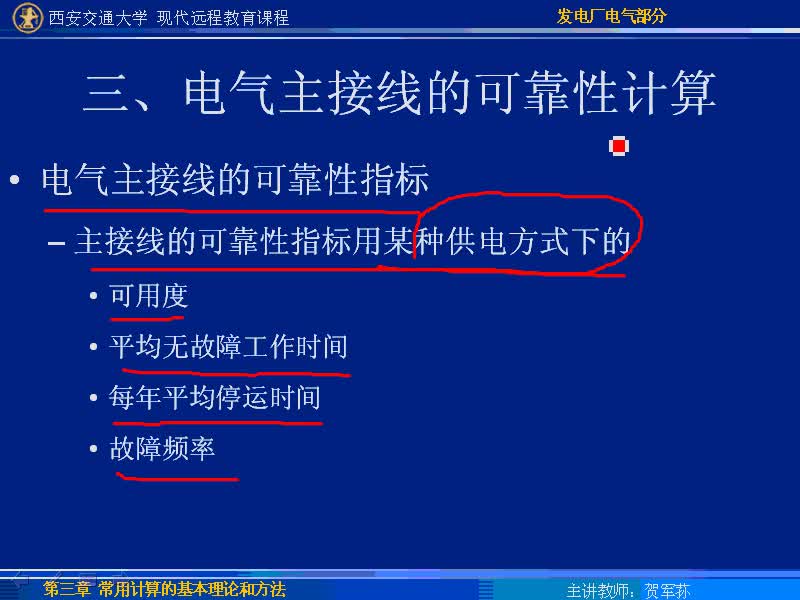
(3)混合系統可靠性模型
實際工程中,為了在成本和可靠性方面求得平衡,常常使用串聯和并聯混合系統。也就是對可靠度較低的單元采用并聯系統,可靠度高的單元保持串聯系統。模型如圖3所示。
混合系統的可靠度:
R(t)=R1(t)·R2(t)·R3-2(t)·R4(t)
如果R1=R2=R4=0.99,R3=0.9
則R3-2=1-[1-R3]2,R3-2=0.99
R=R1·R2·R3-2·R4
=0.96=96%。(F=4%)。
假使,U3不用并聯系統,則R=0.87=87%,(F=13%)。可見,兩者可靠度的差別還是很明顯的,故障率降低了3倍多。混合系統比串聯系統可靠性高,比并聯系統簡單。
3.2改善電子系統的使用環境降低元器件的環境溫度
電子系統的可靠性和使用環境如何有著極為密切的關系。元器件的失效率在不同的使用環境中和其基本失效率差別很大,通常應以環境系數進行修正。美國于上世紀70年代公布了不同元器件的環境系數數值。原有9種環境條件,現只列出較常用和有代表性的4種如下:
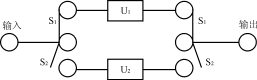
圖2并聯系統模型

圖3混合系統模型
——GB:良好地面環境。環境引力接近于“0”,工程操作和維護良好。
——GF:地面固定式的使用環境。裝在永久性機架上,有足夠的通風冷卻。由軍事人員維修,通常在不熱的建筑內安裝。
——NS:艦船艙內環境。水面艦船條件,類似于GF。但要受偶然劇烈的沖擊振動。
——GM:地面移動式和便攜式的環境。劣于地面固定式的條件,主要是沖擊振動。通風冷卻可能受限制,只能進行簡易維修。
上述環境條件下的環境系數πE如表5所列:
表5環境系數πE
| 元器件類型 | GB | GF | NS | GM | ||
|---|---|---|---|---|---|---|
| 集成電路 | 0.2 | 1.0 | 4.0 | 4.0 | 說明:λp=λb·πE式中:
λp實際使用中的 失效率λb基本 失效率πE環境系數 | |
| 電位器 | 1.0 | 2.0 | 5.0 | 7.0 | ||
| 功率型薄膜電阻器 | 1.0 | 5.0 | 7.5 | 12.0 | ||
| 電容器 | 紙和塑料膜 | 1.0 | 2.0 | 4.0 | 4.0 | |
| 陶瓷 | 1.0 | 2.0 | 4.0 | 4.0 | ||
| 鋁電介 | 1.0 | 2.0 | 12.0 | 12.0 | ||
| 變壓器 | 1.0 | 2.0 | 5.0 | 3.0 | ||
| 繼電器 | 軍用 | 1.0 | 2.0 | 9 | 10 | |
| 下等質量 | 2.0 | 4.0 | 24 | 30 | ||
| 開關 | 0.3 | 1.0 | 1.2 | 5.0 | ||
| 接插件 | 軍用 | 1.0 | 4.0 | 4.0 | 8.0 | |
| 下等質量 | 10 | 16 | 12 | 16 | ||
過高的環境溫度對元器件的可靠性非常有害:
(1)半導體器件(含各種集成電路和二極管,三極管)
例如硅三極管以PD/PR=0.5設計(PD:使用功率,PR:額定功率),則環境溫度對可靠性的影響,如表6所列。
表6環境溫度對半導體器件可靠性的影響
| 環境溫度Ta[℃] | 20 | 50 | 80 |
|---|---|---|---|
| 失效率λ[1/109h] | 500 | 2500 | 15000 |
以UD/UR=0.6設計(UD:使用電壓,UR:額定電壓),則環境溫度對可靠性的影響如表7所列。
表7環境溫度對電容器可靠性的影響
| 環境溫度Ta[℃] | 20 | 50 | 80 |
|---|---|---|---|
| 失效率λ[1/109h] | 5 | 25 | 70 |
以PD/PR=0.5設計,則環境溫度對可靠性的影響如表8所列。
表8環境溫度對碳膜電阻器可靠性的影響
| 環境溫度Ta[℃] | 20 | 50 | 80 |
|---|---|---|---|
| 失效率λ[1/109h] | 1 | 2 | 4 |
可見,加強通風冷卻十分有益于電子系統的可靠性。國內有些部門(如鐵路)要求系統有很高的可靠性,又明令不許使用風扇進行強迫通風冷卻。結果不僅設備成本提高,可靠性也難以真正保證,人為地造成了許多問題。其實,現在優質的風扇可以保證50000~60000h的使用壽命(相當于連續運行6年以上)。更換風扇比其他部件的維修也省力省時得多。只要在系統設計條件中,規定風扇即使不工作,設備依然可以長期正常運行。那么,加強通風冷卻,絕對有利于可靠性,何樂而不為!
3?3減小元器件的負荷率是改善失效率的捷徑
元器件實際工作中的負荷率和失效率之間存在著直接的關系。因而,元器件的類型,數值確定以后,應從可靠性的角度來選擇元器件必須滿足的額定值。如半導體器件的額定功率、額定電壓、額定電流,電容器的額定電壓,電阻器的額定功率等等。
(1)硅半導體器件
環境溫度Ta=50℃,PD/PR對頻率的影響如表9所列。
表9PD/PR對硅半導體器件失效率的影響
| PD/PR | 0 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
|---|---|---|---|---|---|---|---|---|
| λ[1/109h] | 30 | 50 | 150 | 700 | 2500 | 7000 | 20000 | 70000 |
(2)電容器
英國曾發表電容器失效率λ正比于工作電壓的5次方的資料,稱為“五次方定律”,即λ∝U5。
當U=UR/2,
λ=λR/25=λR/32(λR為額定失效率)
當U=0.8UR=UR/1.25,
λ=λR/(1.25)5=λR/3.05
當電容器工作電壓降低到額定值的50%時,失效率可以減小32倍之多。
(3)碳膜電阻器
環境溫度Ta=50℃,美國于上世紀70年代實際使用的軍品數據如表10所列。
表10PD/PR對碳膜電阻器失效率的影響
| PD/PR | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 |
|---|---|---|---|---|---|---|
| λ[1/109h] | 0.25 | 0.5 | 1.2 | 2.5 | 4.0 | 7.0 |
以上數據表明為了保證可靠性,必須減小元器件的負荷率。例如:美國“民兵”洲際導彈的電子系統規定元器件的負荷率為0.2。
實際使用中的經驗數據為:
——半導體元器件負荷率應在0.3左右;
——電容器負荷率(工作電壓和額定電壓之比)最好在0.5左右,一般不要超過0.8;
——電阻器、電位器、負荷率≤0.5。
總之,對各種元器件的負荷率只要有可能,一般應保持在≤0.3。不得已時,通常也應≤0.5。
3?4簡化電路,減少元器件的數量,盡量集成化,認真選用高可靠性的元器件,是提高可靠性的最基本思路
電子系統可靠度
R=R1·R2·R3……RN(0≤R≤1)。
電子系統的失效率
λ=n1·λ1+n2·λ2+n3·λ3……nN·λN.(λ≥0)
顯然,元器件數量越多越不可靠。
假如每個元器件Ri=0.999,共有5000個元器件,則R=0.9995000=0.01,顯然極不可靠。
若元器件數量減到1800個,則R=0.9991800=0.19。說明如能做到元器件減少64%,可靠度將增加19倍。
因而應盡量采用集成化的器件。如一只集成電路可以代替成千上萬只半導體三極管和二極管等器件,從而極大地提高了可靠性。
還應注意到選用高可靠性的元器件類型和品質檔次的重要意義。例如功能相似的電容器,云母介質的失效率就要比玻璃或陶瓷介質的低30倍左右。同類的元器件,不同品質檔次,如軍品和民品,上等質量和下等質量,在同樣的功能和條件下,失效率也會差3~10倍,選用應慎之又慎。
可以說,在保證相同功能和使用環境的條件下,越簡化的電路,越少的元器件,系統就越可靠。
例如:某公司1000VA高品質交流參數穩壓電源,使用于GM環境條件(移動,車載,通風不理想,不便維修)。也能保證MTBF≥20萬h。主要原因就是電路簡單,元器件數量少。整臺電源只包括:
——特種變壓器1只
基本失效率為λ1=300×10-9/h。
——金屬化薄膜電容器2只
基本失效率為λ0=830×10-9/h。
電容器負荷率為0.8。所以,
λ2=(830/3.05)×10-9/h。
——焊接點20個
基本失效率為λ3=5.7×10-9/h。
因而:λΣ=λ1+2λ2+20λ3
=[300+544+114]×10-9/h
=958×10-9/h。
使用于GM環境條件,平均πE=4,
λΣP=λΣ·πE=3832×10-9/h。
平均無故障工作時間
MTBF=1/λΣP=(1/3832)×109/h
=26×104h=26萬h
≥20萬h。
年可靠度:P=1/eλΣP·8760=0.967=96.7%
故障率:F=1-P=3.3%
公司長期生產實踐的統計數字也證明,該類電源的MTBF≥20萬h。
當然,使用在其他環境條件,可靠性會更好。
3?5重視元器件的老化工作減少系統的早期失效率
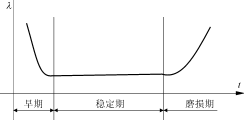
元器件、設備、系統的失效率在整個使用壽命中并非是恒定不變的常數,通常存在著如圖4所示的“浴盆曲線”。
(1)早期通常早期失效率會比穩定期的失效率高得多。造成失效的原因是元器件制造過程中的缺陷和裝機的差錯或不完善的連接點或元器件出廠時漏檢的不合格產品混入所致。因而一定要先使設備運行一個時期,進行老化,使早期失效問題暴露在生產廠老化期間。給用戶提供的是已進入穩定期的可靠產品。
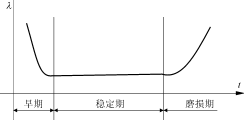
圖4失效率與時間的關系曲線
老化的時間,日本的民用產品(如電視機)一般不小于8h。而美國宇宙飛船規定每個元器件裝上飛船之前老化50h,裝上飛船以后,又老化250h,共300h。以淘汰有隱患的元器件,保證工作可靠性。實際工作中,對可靠性要求較高的設備老化時間確定在20~50h較為合適。
(2)穩定期此時失效率λ近于常數,用作正常使用期。也可根據失效率λ來預算設備的其他可靠性指標。通常,在較好的使用環境中,如果一旦出現故障能得到及時和正確的維修,則電子系統的穩定期應不短于6~8年。
(3)磨損期設備使用的壽命末期,由于元器件的材料老化變質,或設備的氧化腐蝕、機械磨損、疲勞等原因造成。失效率λ將逐步增加,進入不可靠的使用期。磨損期出現的具體時間,受各種因素影響,很不一致。設計合理,元器件質量選擇較嚴,環境條件不太惡劣的設備磨損期出現的時間會晚得多。
4結論
保證設備的可靠性是一個復雜的涉及廣泛知識領域的系統工程。只有給予充分的重視和認真采取各種技術措施,才會有滿意的成果。其基本點為:
(1)高可靠度的復雜系統,一定要采用并聯系統
的可靠性模型。系統內保有足夠冗余度的備份單元,可以進行自動或手動切換。如果功能上允許,冷備份單元切換,較熱備份單元切換,更能保證長期工作的可靠性。
(2)任何電子系統都不可能100%地可靠。設計
中應盡量采用便于離機維修的模塊式結構,并預先保留必要數量(通常為5%)的備件。以便盡量縮短平均維修時間MTTR。使有效度A近于100%。
(3)加強通風冷卻,改善使用環境是成倍提高可
靠性的最簡便和最經濟的方法。
(4)簡化電路,減少元器件的數量,減輕元器件的
負荷率,選用高可靠的元器件是保證系統高可靠的基礎。
(5)重視設備老化工作,減少系統早期失效率。
相信,通過精心設計,認真生產,嚴格質檢,及時維修,完全可以使電子系統(含電源設備)達到十分接近于100%的可靠度。滿足國防,科研,工業等各方面的需求,并進而走向世界。
 電子發燒友App
電子發燒友App































評論