壓敏電阻主要可用于直流電源、交流電源、低頻信號線路、帶饋電的天饋線路,壓敏電阻一般并聯在電路中使用,壓敏電阻也可以很簡單地串聯使用,但是將壓敏電阻接入電路的連接線要足夠粗。
2016-10-19 17:43:44 13289
13289 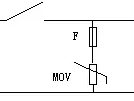
matlab2013b 用前饋控制的simulink仿真,有些模塊連接不上 在連接線上顯示 fim 請指點
2015-06-19 16:45:13
跟著人們對多媒體和3g手機的希望越來越高,對高畫質的視頻、音頻的播映、多媒體的數據流、更加明晰的顯現及更多文娛等等的要求,手機中的功用和使用的多元化,以及功率耗費的增加,電源辦理IC也就成了手機
2018-08-17 15:10:32
必須注意。盡可能減小線路電感圖1是用于評估電源轉換器的設置原理圖。我們要測試的是電源電路的行為,而不是測試板與實驗室電源之間或與輸出端負載之間的連接線路的影響。為降低這些連接線路的影響,應采取兩項
2019-12-16 09:58:00
原理圖中連接好的線路,轉換到PCB中的時候一定會有連接線嗎?比如說原理圖中的R3中間接了ADC0804,但是PCB中的R3一根連接線都沒有
2020-12-19 16:23:40
`如圖片所示,我明明把所有的網絡都聯通了,怎么在板外還有這樣的連接線?而且那些地方什么元件什么網絡都沒有,請壇子里哪位大俠指點啊!`
2015-07-28 10:07:51
在CAD繪圖過程中,如果想要連接兩條線段的話該如何操作呢?其實很簡答,接下來的CAD教程就和小編一起來了解一下浩辰CAD建筑軟件中CAD線段連接的相關操作技巧吧!CAD連接線段的操作步驟:浩辰CAD
2021-06-06 20:33:05
新手,剛買了一臺DLP4500,知不道用什么連接線才可以與電腦連接起來,求指教!
2019-05-27 17:36:43
FFC連接線 24P 間距1.0mm長8CM 同向
2023-03-25 00:41:51
FFC連接線 6P 間距1.0mm長10CM 同向
2023-03-25 00:41:51
HDMI連接線http://www.gooxian.com/ArticleDetails.aspx?ArticleId=504在2002年首次開發,經過過去十年的發展,HDMI線發展成一個能傳輸
2017-08-14 10:25:55
HDMI是建立在DVI基礎上的數字視頻線材,DVI線能傳輸數字視頻數據,而HDMI連接線則在此基礎上還能承載音頻。http://www.gooxian.com/ArticleDetails.aspx
2017-08-11 09:07:32
Labview流程圖中,有好幾種連接線。顏色各異,粗細也不一樣,請問這代表的是數據類型嗎?各種顏色各是什么類型的?我們老大說是這樣的,但我看著不像,請高手指點
2012-12-02 23:40:08
普通串口線2和3是交叉相連的,市場上也有不是交叉相連的DB9接口的連接線,當然從外觀上看樣子和交叉相連的普通串口線是一樣的,只能用萬用表測才能測出來。這兩種線我現在都有。交叉相連的用于串口通信,不交
2009-08-24 22:25:08
我看了許多仿真圖都沒有連接線,請問是怎樣連在一起的?
2015-07-19 20:26:36
買的潤和的Hi3559A開發板有沒有sensor連接線序圖?買了個imx334連上板子后連接線發燙,想看看是不是板子和相機的接線序列不對。
2022-03-02 15:04:36
`什么是橋架連接線,就是將分段的橋架連接起來的接地線,所以很多人也叫它橋架接地線。幾年前,人們還會用純銅線來搭接橋架,隨著市場競爭越來越激烈,價格戰也出現了白熱化,在人工成本不降反升的前提下,只能
2019-02-20 15:01:34
是兩個金屬體(機柜、橋架、線槽、鋼筋、金屬管等)之間的接地金屬連接體(導線、圓鋼、扁鋼、扁銅等)。指接地母線遇有障礙(如建筑物伸縮縫,沉降縫等)需跨越時相連接的連接線,或利用金屬構件,金屬管道作為接地線
2018-06-16 10:02:54
`各位大佬,請問一下這個連接線叫什么,哪里可以購買到?`
2019-09-09 19:14:01
如何快速產生 這條連接線表達錯誤
2019-09-03 01:39:43
如何用萬用表測LVDS連接線的針腳
2013-04-24 16:32:28
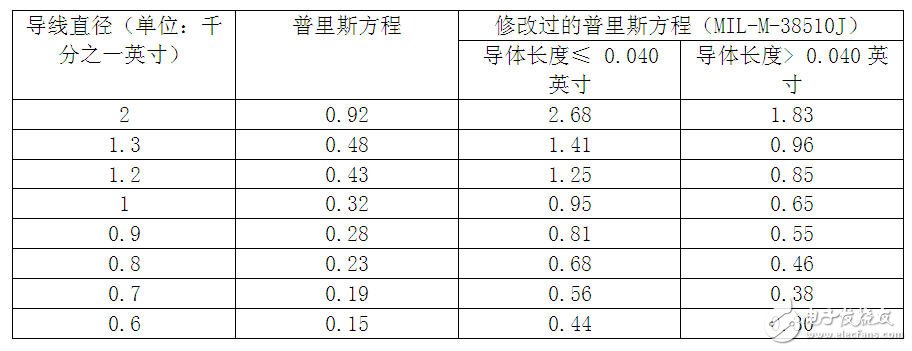
×規格- 10.8))導線電阻 在導線規格表中常會提供相關規格的一些參數值。通過這些參數值可以估計某一長度導線的電阻。而連接線電阻的計算比導線電阻的計算稍微復雜。每種金屬都有一個電阻系數(有時也稱為特征
2013-08-28 16:49:08
可以計算出連接線的橫截面面積:面積 = l/(10(10×規格- 10.8))導線電阻 在導線規格表中常會提供相關規格的一些參數值。通過這些參數值可以估計某一長度導線的電阻。而連接線電阻的計算比導線
2018-11-26 16:57:47
我畫好電路圖后導入網絡表卻沒有連接線,請問哪位高手知道請解釋一下只有幾條線連接了其它的沒有,我檢查過圖紙沒有地方錯啊難道要設置哪里嗎?請指點,怎么設置啊
2012-03-30 21:26:30
連接等。產品運用:跨接線,連接線是兩個金屬體(機柜、橋架、線槽、鋼筋、金屬管等)之間的接地金屬連接體(導線、圓鋼、扁鋼、扁銅等)。`
2019-02-26 11:48:08
1.未讀取發動機電控單元(ECU)記錄的故障碼之前不能拆除蓄電池連接線 因為在讀取故障代碼之前便貿然拆下蓄電池連接線或拔下電源保險絲,由于中斷ECU的電源,存儲在其隨機存儲器中的故障代碼便會自動
2012-05-19 11:26:10
1.未讀取發動機電控單元(ECU)記錄的故障碼之前不能拆除蓄電池連接線 因為在讀取故障代碼之前便貿然拆下蓄電池連接線或拔下電源保險絲,由于中斷ECU的電源,存儲在其隨機存儲器中的故障代碼便會自動
2012-05-19 11:28:43
`東莞市雅杰電子材料有限公司產品運用:跨接線,連接線是兩個金屬體(機柜、橋架、線槽、鋼筋、金屬管等)之間的接地金屬連接體(導線、圓鋼、扁鋼、扁銅等)。接地跨接線:防雷接地應該形成一個閉和回路后接
2019-02-26 11:52:31
請問大佬們有哪些可以耐高溫的連接線以及插座(產品都是2.54mm排針做的引腳),有沒有現成的連接線(2.54mm雙排座),或者代加工廠商推薦。
2017-04-20 17:16:03
`如圖片,有大佬認識這是什么運動控制卡的連接線嗎?目前有一根連接線,需要配一塊運動控制卡,緊急請教`
2019-09-19 15:51:19
`橋架跨接線是由銅編織帶作為導體,兩端用接線端子壓接的銅連接線,其主要作用就是防靜電接地連接。訂做廠家:東莞市卡諾電氣科技有限公司咨詢熱線:唐小姐***`
2018-05-18 18:35:38
top層 用的是正片鋪銅 焊盤與銅皮十字連接線大小已設好想調節個別焊盤十字花連接線寬度 發現無法刪除 但可以通過走線(設置走線寬度大小取代十字連線)連接 達到改變個別十字花連接線 不知這樣可否 經驗不足 請求指教 感激至極!!!
2014-06-12 15:27:59
電動三輪電機和控制器的連接線溫度很高是為什么?怎么解決呢?
2023-03-16 10:52:19
`東莞雅杰電子材料有限公司產品運用:跨接線,連接線是兩個金屬體(機柜、橋架、線槽、鋼筋、金屬管等)之間的接地金屬連接體(導線、圓鋼、扁鋼、扁銅等)。接地跨接線:防雷接地應該形成一個閉和回路后接地,在
2019-02-26 11:35:10
`東莞市雅杰電子材料有限公司產品運用:跨接線,連接線是兩個金屬體(機柜、橋架、線槽、鋼筋、金屬管等)之間的接地金屬連接體(導線、圓鋼、扁鋼、扁銅等)。銅編織帶/線采用銅圓絲或鍍錫銅圓絲編織而成的帶狀
2019-02-26 14:33:23
西門子伺服驅動與電機編碼器連接線最長能達到多少米?哪位大神做過長距離傳輸的請指導一下!!!!!!
2023-11-07 06:21:50
stm32f10x.h連接線的定義是什么?stm32f10x.h連接線的內存映射是什么?
2021-11-01 07:27:05
請問AD8342評價板上的黃色金屬接口對應什么型號的連接線?
謝謝~
2023-12-18 07:43:22
拖動器件不讓連接線跟著一起走,怎么設置呢?
2019-03-06 00:16:23
如何隱藏pcb里的連接線(飛線),有時候走線看上去很亂
2019-04-30 02:19:51
)之間的接地金屬連接體(導線、圓鋼、扁鋼、扁銅等)指接地母線遇有障礙(如建筑物伸縮縫,沉降縫等)需跨越時相連接的連接線,或利用金屬構件,金屬管道作為接地線時需要焊接的連接線。常見的接地跨線有伸縮(沉降)管道法蘭,吊車鋼軌接地跨接線等,計算工程量按“處”為單位。 `
2018-12-17 11:02:19
`按照目前不同級別的連接線及使用標準,確實在能夠有效調控的領域內獲得更多的應用。關鍵是對于安全的防護,畢竟現在已經在很多領域內都已經具備足夠的操作指標,尤其是在防水連接線的整體范圍內確實需要有更加
2017-04-10 16:56:31
、游船、工業設備、通信設備、探測設備等等,都需要用到防水線。 還廣泛應用于舞臺燈、水族、衛浴、開關電源、機電設備等需要防水連接等方面。 防水連接線也就是帶線的防水插頭,防水插頭也有帶線不帶線的,只是
2017-06-01 17:11:05
音頻連接線,簡稱音頻線;用來傳輸電聲信號或數據的線。廣義的來說有電信號與光信號兩大類。
2019-09-26 09:00:49
BVR黃綠接地線/配電箱接地線/純銅黃綠接地線連接線用于電纜橋架接地,配電箱接地,KBG管連接線,光伏電板連接,電器接地材質:BVR黃綠線(國標 2.5 /4/6平方)綠雙色光伏板電線2.5平方30厘米
2018-10-26 17:17:46
aterla下載電纜連接線 (帶PCB文件)
2009-01-16 09:18:05 17
17 在電腦的使用中往往會遇到各種各樣的連接線。這些連接線外觀上好像都差上多,但內部結構完全上同并且上能混用。如果在使用中這些連接線壞了,往往很多使用者都上知道應該
2009-12-01 11:54:56 33
33 電腦串口、并口連接線大全
在電腦的使用中往往會遇到各種各樣的連接線。這些連接線外觀上好像都差
2010-02-06 10:46:51 83
83 連接線轉接卡 計算機主機和
2009-12-28 13:59:47 793
793 連接線轉接卡的產品類型
2009-12-28 14:04:58 1023
1023 實現電路板連接線的規格化
導線的規格參數可以很容易地從各種資料中獲得,但如何用這些參數來計算印制板連接線的電阻呢?本文
2010-10-04 17:21:28 2551
2551 使用中往往會遇到各種各樣的連接線。這些連接線外觀上好像都差不多,但內部結構完全不同并且不能混用。
2012-04-01 14:26:43 2054
2054 為了將車載MP3連接到電腦,自制一“雙公頭USB連接線”
2012-06-03 12:07:31 63368
63368 
電子發燒友網: 為了能夠將車載MP3連接到電腦上,本文介紹了一種自制雙公頭USB連接線的方法,不僅材料簡單,制作也很簡單。您如果有兩個壞鼠標的話,不妨試試...
2012-07-06 09:58:46 0
0 電子發燒友網: 為了能夠將車載MP3連接到電腦上,本文介紹了一種自制雙公頭USB連接線的方法,不僅材料簡單,制作也很簡單。您如果有兩個壞鼠標的話,不妨試試... DIY材料必備: 兩
2012-07-06 09:51:54 13052
13052 目前主要有三種,HDMI連接線、VGA連接線以及DVI連接線。現在基本上都會選擇有HDMI接口(高清接口)的顯示器,那么選擇一條好的HDMI線就顯得非常的重要。
2019-07-02 16:46:36 4866
4866 顯示器應該選擇什么連接線呢?這是由顯卡顯示接口與顯示器顯示接口來決定的,但因為很多用戶不了解這些接口的知識,那么就無法選擇顯示器連接線。
2019-07-05 11:25:52 4114
4114 45cm優質彩色鱷魚夾試驗連接線可配合面包板、面包線制作電子積木,連接方便,是電子愛好者的必備線材。
2019-12-03 17:02:11 2941
2941 
Shiftout專用連接線 ,能將Shiftout Module、SPI LED、SPI LCD連接到Interface shield上。
2019-12-01 10:26:22 1150
1150 
IIC接口模塊專用連接線 ,能將IIC接口的模塊連接到Interface shield上。
2019-12-02 09:30:37 1159
1159 
進口優質連接線,長度30cm,一頭3芯PH2.0插頭,一頭3芯杜邦插頭。
2019-12-02 09:35:47 1011
1011 
TLC5940專用連接線 ,能將RGB LED Module連接到Interface shield上。
2019-12-02 09:36:45 1296
1296 
進口優質連接線,長度30cm,一頭3芯PH2.0插頭,一頭3芯杜邦插頭。
2019-12-04 14:18:28 1086
1086 
根據消息報道,聯力在CES 2020上展示了新款的Strimer Plus RGB 24pin電源連接線,可以呈現出涌動的RGB效果。
2020-01-17 15:45:22 3256
3256 顯示器連接線包括連接主機和顯示屏的數據線纜,連接電源的電源線纜。
2020-12-22 16:51:39 11427
11427 防水連接線的防水質量問題一直是關鍵,因為連接線的防水性能在市場上已經成為了電子產品的主要品質要求之一,所以在設計防水連接線時,需確保其防水性能符合規范要求,下面聚飛電子線束廠家為大家講解防水連接線
2021-01-10 10:33:42 2128
2128 大家都知道端子設計精密,輕微的碰觸就會導致變形,這種變形,輕則會導致裝配困難,嚴重的會引起電器性能不良。接下來介紹,專業的端子連接線加工廠是如何做到端子連接線防護的! 端子來料的時候大多數
2021-01-13 13:42:40 2683
2683 1.8米版的價格是949元;而雷靂4 Pro連接線3米版的售價則高達1169元。 很多網友估計都要吐槽了,一根連接線就要來收割韭菜了嗎? 這個節奏是蘋果推出的145元的擦屏布還遠遠不夠;現在要推超千元的連接線,就是不知道哪些人會買單,蘋果的品牌就這么好使啊。 根據蘋果公司的官網
2022-03-10 19:00:31 2027
2027 
電子連接線是非常普遍的電子產品,類型多樣,選擇連接線產品,康瑞連接器廠家建議大家從這幾點來看。
2023-01-31 14:56:14 1590
1590 每個連接線產品都需要具備堅固耐用的端子,端子的主要作用是通過端接導體來建立電連接,本文康瑞連接器廠家工程師主要為大家分享連接線與端子配對時的考慮問題。
2023-02-06 16:46:22 185
185 在當今的科技時代,可以說很多電子產品和電子行業都需要用到電子線束、連接線。平時我們看到一條條的連接線和電子線束大家知道是怎么生產出來的么?下面康瑞連接器廠家為大家講解連接線、電子線束等的生產流程。
2023-02-17 13:57:32 750
750 在日常生活中,端子連接線常用于我們的家用電器,像燈飾照明,智能家居,小家電等都離不開端子線的使用。端子線一般用于電器內部連接。端子連接線常見問題有哪些?今天就和康瑞連接器廠家一起來了解。
2023-03-09 15:58:05 614
614 由于汽車行業的特殊性,汽車連接線的制造工藝也比其他普通線束更特殊。
淺談汽車連接線
隨著電子控制技術的普遍使用,電氣元件和電線的數量將繼續增加,線束將變得更厚和更重。為此,國內領先的汽車
2023-03-24 10:40:48 642
642 M8航空插座防水連接線具有優異的防水性能,能夠在惡劣的環境下保障設備連接的可靠性。連接線接口采用M8標準接頭,大小合適,連接穩定可靠。連接線外層采用聚氨酯材料制作,具有良好的耐腐蝕性和耐磨性,能夠
2023-04-17 10:42:02 1038
1038 
【電蜂優選】FAKRA連接線的作用主要是保證汽車的高壓互聯系統,即在內部電路被阻斷或隔離的地方搭建一座橋梁,讓電流通過。
2023-03-20 09:36:06 1968
1968 
HSL連接線是一種常用的電子連接器件,廣泛應用于計算機、通信、家電等電子設備中。
2023-05-06 10:44:19 342
342 
在選擇LVDS連接線時,需要根據實際需求選擇合適的規格和參數。例如,根據設備的工作環境、電流、電壓等參數選擇合適的LVDS連接線。
2023-05-29 09:28:38 379
379 
隨著電動汽車和混合動力汽車等新能源汽車的普及,LVDS連接線的使用也越來越頻繁。LVDS連接線作為汽車中重要的電氣接口之一,其性能和質量直接影響到車輛的安全性和可靠性。
2023-05-29 09:36:01 296
296 
LVDS連接線接插周期是指LVDS連接線插入和拔出設備的時間間隔。LVDS連接線的接插周期一般由設備的使用頻率和LVDS連接線的設計壽命決定。
2023-05-30 10:47:09 309
309 
在選用LVDS連接線時,需要考慮環境因素,包括溫度、濕度、振動、污染等。一般來說,高溫、高濕、高污染的環境會對LVDS連接線造成較大的影響,因此在選用LVDS連接線時需要考慮其耐環境性能。
2023-05-31 10:08:37 269
269 
需要檢查高壓連接線的外觀是否完整。檢查高壓連接線是否有損壞、變形或破損的情況。如果高壓連接線存在損壞或變形,可能會導致網絡傳輸不穩定或無法傳輸數據。此外,還需要檢查高壓連接線的金屬接觸件是否干凈,如果有灰塵或污垢,可能會導致接觸不良,影響網絡傳輸速度和穩定性。
2023-07-11 17:49:04 266
266 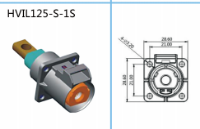
端子連接線是一種常見的電氣連接方式,用于連接電線或導線的末端,并實現電氣連通性。接頭是用于連接兩根或多根電線末端的裝置,它能夠確保連接的可靠性和安全性。
2023-07-12 10:33:30 2242
2242 高壓連接線插針端子由插針和端子組成,通常用于連接電路板和其他電子元器件。插針是高壓連接線插針端子的核心部分,它是一種金屬針,用于插入電路板或其他設備上的插座孔。
2023-07-17 18:00:01 621
621 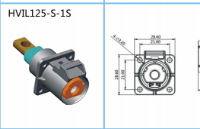
高壓連接線的主要功能是傳輸電流和信號,因此,電氣性能是高壓連接線材料選擇的首要因素。高壓連接線材料的電阻、電容、電感等電氣性能都會對電流和信號的傳輸產生影響。
2023-07-19 11:34:24 446
446 
高壓連接線需要防靜電。靜電對高壓連接線的危害在于它能夠瞬間放電,產生高電壓,產生強電磁場,使連接器產生誤動作,損壞元件,導致產品質量問題。
2023-07-20 17:22:03 714
714 
高壓連接線通常用于連接高壓電器設備,例如變壓器、斷路器、開關設備等。為確保高壓連接線的安全性和可靠性,需要進行適當的保養。
2023-07-21 11:31:42 1025
1025 
高壓連接線的可分離性在許多應用場景中都非常有用。例如,在航空航天領域,高壓連接線經常需要安裝在狹小的空間中,插拔高壓連接線時需要小心避免插針或插孔受到損壞。
2023-07-26 09:53:42 363
363 
連接線老化是電子設備電氣系統故障的常見因素之一。在使用過程中,惡劣的作業環境與作業條件往往會使連接線加速老化,其中常見的老化的因素包括機械力損害、絕緣受潮、腐蝕、超負荷使用等因素。 機械力損害主要
2023-08-03 16:54:01 357
357 
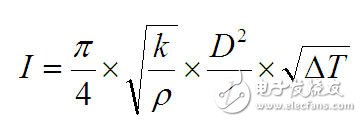
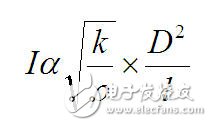
 電子發燒友App
電子發燒友App









































評論