1、回路電流法的原理
一個(gè)聯(lián)通圖,支路數(shù) b ,節(jié)點(diǎn)數(shù) n ,樹支數(shù) ( n - 1 ) ,連支數(shù) b - ( n - 1 );
選定一個(gè)樹,加上一個(gè)連支,就構(gòu)成一個(gè)回路,指定回路電流為 i l1,也稱為連支電流。對(duì)此回路應(yīng)用 KVL ,得一 KVL 方程;
加上第二個(gè)連支,就構(gòu)成第二個(gè)回路,指定回路電流為 i l2,對(duì)此回路應(yīng)用 KVL ,又得一 KVL 方程;
…………
最后得到:(b - n + 1) 個(gè)回路電流變量,和同樣多的 KVL 方程;連立求解得各回路/連支電流;再疊加求出各支路電流。
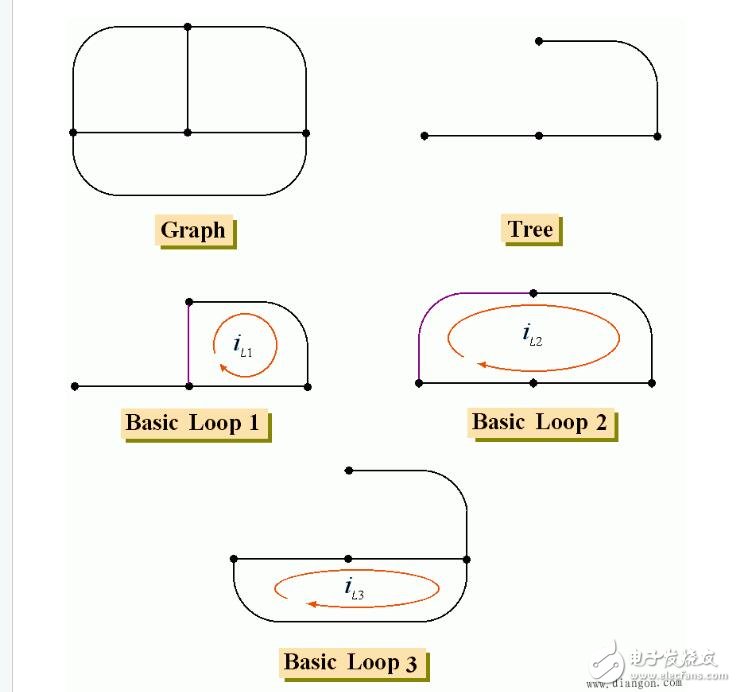
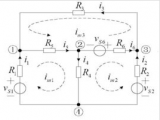
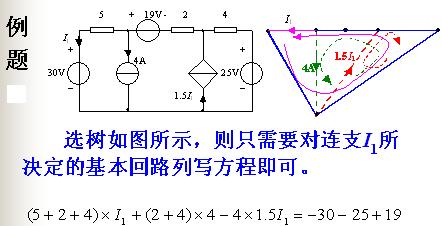
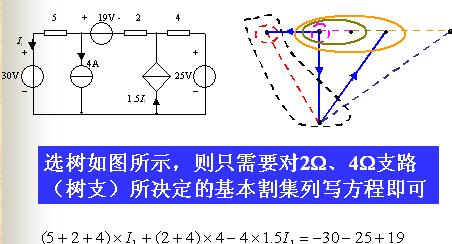
如果象下圖粗線所示選取樹,則基本回路就是三個(gè)網(wǎng)孔。這說明回路電流法比網(wǎng)孔電流法更普遍。
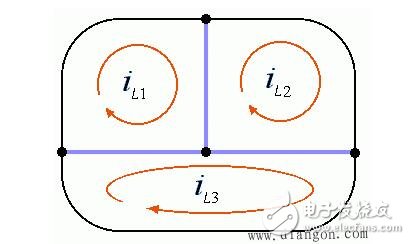
2、回路電流法
以基本回路中的回路電流為未知量列寫電路方程分析電路的方法。當(dāng)取網(wǎng)孔電流為未知量時(shí),稱網(wǎng)孔法。
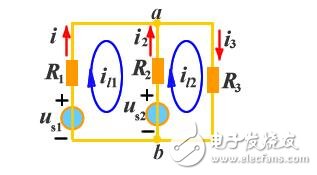
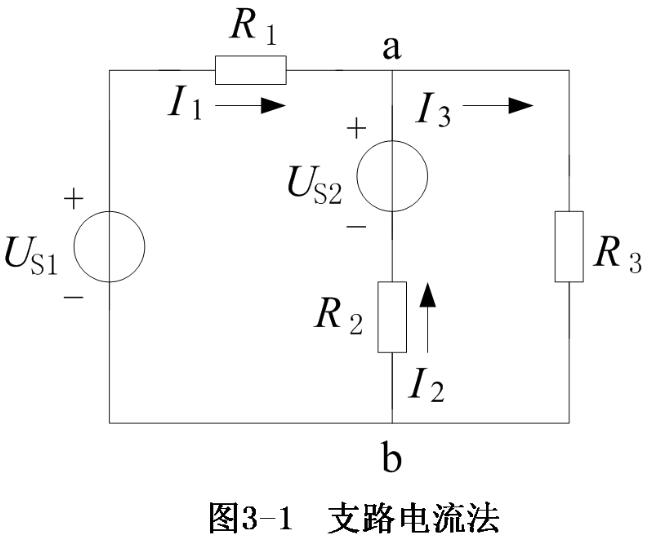
1)支路電流與回路電流的關(guān)系
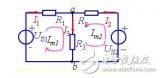
上圖所示電路有兩個(gè)獨(dú)立回路,選兩個(gè)網(wǎng)孔為獨(dú)立回路,設(shè)網(wǎng)孔電流沿順時(shí)針方向流動(dòng),如圖所示。可以清楚的看出,當(dāng)某支路只屬于某一回路(或網(wǎng)孔),那么該支路電流就等于該回路(網(wǎng)孔)電流,如果某支路屬于兩個(gè)回路(或網(wǎng)孔)所共有,則該支路電流就等于流經(jīng)該支路兩回路(網(wǎng)孔)電流的代數(shù)和。如上圖電路中:
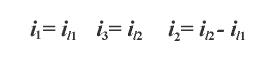
2)回路電流法列寫的方程
回路電流在獨(dú)立回路中是閉合的,對(duì)每個(gè)相關(guān)節(jié)點(diǎn)回路電流流進(jìn)一次,必流出一次,所以回路電流自動(dòng)滿足KCL。因此回路電流法是對(duì)基本回路列寫KVL方程,方程數(shù)為:b-(n-1)
與支路電流法相比,方程數(shù)減少n-1個(gè)。
3、回路電流法方程的列寫
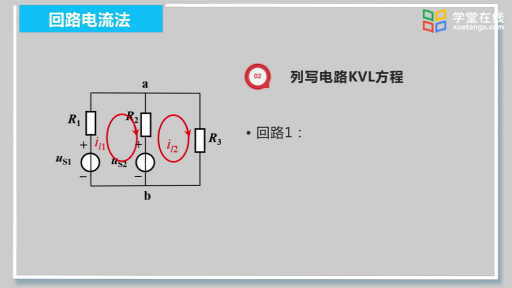
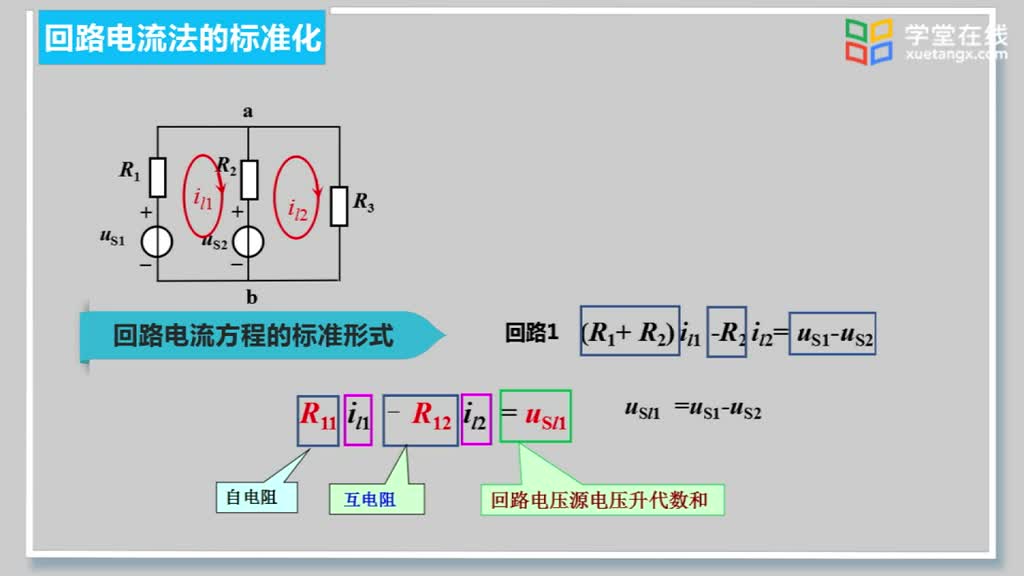
應(yīng)用回路法分析電路的關(guān)鍵是如何簡(jiǎn)便、正確地列寫出以回路電流為變量的回路電壓方程。以上圖電路為例列寫網(wǎng)孔的KVL方程,并從中歸納總結(jié)出簡(jiǎn)便列寫回路KV方程的方法。
按網(wǎng)孔列寫 KVL 方程如下:
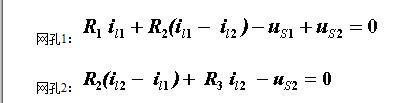
將以上方程按未知量順序排列整理得:
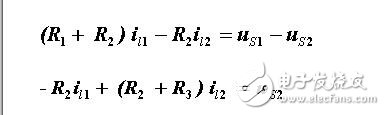
觀察方程可以看出如下規(guī)律:
第一個(gè)等式中,il1前的系數(shù) ![]() 是網(wǎng)孔1中所有電阻之和,稱它為網(wǎng)孔1的自電阻,用R11表示;il2前的系數(shù)
是網(wǎng)孔1中所有電阻之和,稱它為網(wǎng)孔1的自電阻,用R11表示;il2前的系數(shù)![]() 是網(wǎng)孔1和網(wǎng)孔2公共支路上的電阻,稱它為兩個(gè)網(wǎng)孔的互電阻,用R12表示,由于流過R2的兩個(gè)網(wǎng)孔電流方向相反,故R2前為負(fù)號(hào);等式右端
是網(wǎng)孔1和網(wǎng)孔2公共支路上的電阻,稱它為兩個(gè)網(wǎng)孔的互電阻,用R12表示,由于流過R2的兩個(gè)網(wǎng)孔電流方向相反,故R2前為負(fù)號(hào);等式右端![]() 表示網(wǎng)孔1中電壓源的代數(shù)和,用uS11表示,uS11中各電壓源的取號(hào)法則是,電壓源的電壓降落分向與回路電流方向一致的取負(fù)號(hào),反之取正號(hào)。用同樣的方法可以得出等式2中的自電阻、互電阻和等效電壓源分別為:
表示網(wǎng)孔1中電壓源的代數(shù)和,用uS11表示,uS11中各電壓源的取號(hào)法則是,電壓源的電壓降落分向與回路電流方向一致的取負(fù)號(hào),反之取正號(hào)。用同樣的方法可以得出等式2中的自電阻、互電阻和等效電壓源分別為:
自電阻![]() 互電阻
互電阻![]() 等效電壓源
等效電壓源![]()
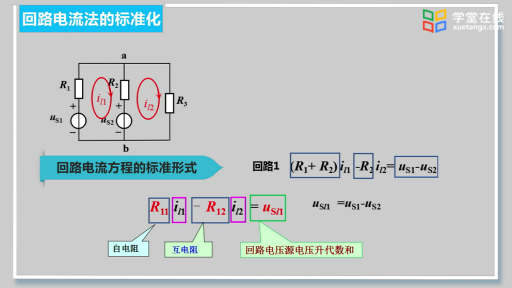
由此得回路(網(wǎng)孔)電流方程的標(biāo)準(zhǔn)形式:
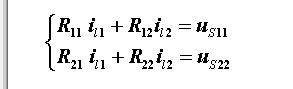
結(jié)論:對(duì)于具有l(wèi)=b-(n -1) 個(gè)基本回路的電路,回路(網(wǎng)孔)電流方程的標(biāo)準(zhǔn)形式:
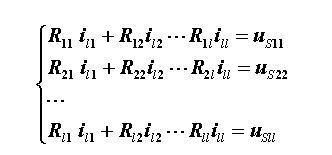
其中: 自電阻Rkk為正;
互電阻 Rjk=Rkj可正可負(fù),當(dāng)流過互電阻的兩個(gè)回路電流方向相同是為正,反之為負(fù);
等效電壓源uSkk中的電壓源電壓方向與該回路電流方向一致時(shí),取負(fù)號(hào);反之取正號(hào)。
注:當(dāng)電路不含受控源時(shí),回路電流方程的系數(shù)矩陣為對(duì)稱陣。
回路法的一般步驟:
(1) 選定l=b-(n -1)個(gè)基本回路,并確定其繞行方向;
(2) 對(duì)l個(gè)基本回路,以回路電流為未知量,列寫 KVL 方程;
(3) 求解上述方程,得到l個(gè)回路電流;
(4) 求各支路電流(用回路電流表示 ) ;
(5) 其它分析。
注:電路中含有理想電流源和受控源時(shí),回路方程的列寫參見例題。
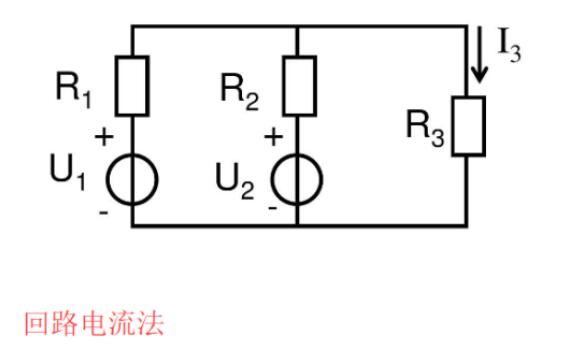
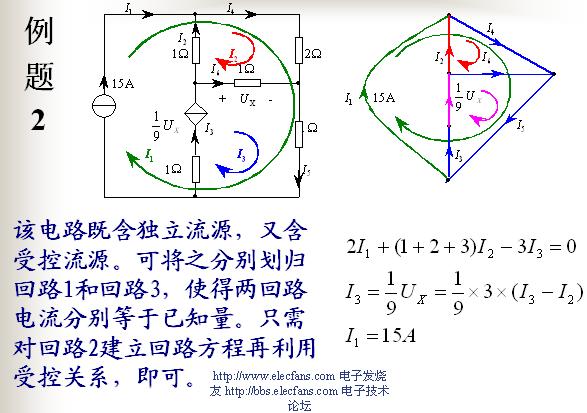
例題 列寫如下電路的回路電流方程,說明如何求解電流 i.
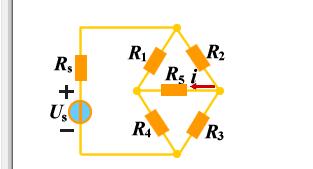
解1:
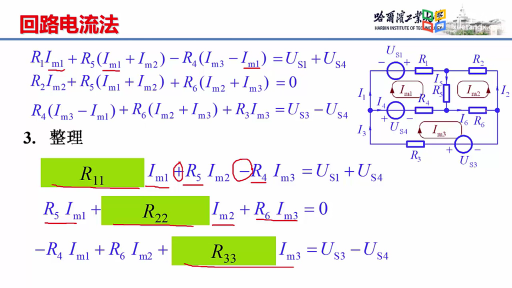
獨(dú)立回路有三個(gè)。選網(wǎng)孔為獨(dú)立回路如圖所示,回路方程為:

從以上方程中解出網(wǎng)孔電流1和網(wǎng)孔電流2,則電流![]()
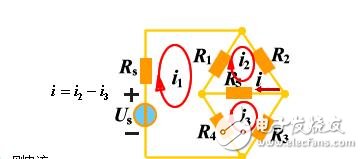
選網(wǎng)孔為獨(dú)立回路
注:本題結(jié)果說明:
(1)不含受控源的線性網(wǎng)絡(luò),回路方程的系數(shù)矩陣為對(duì)稱陣,滿足 Rjk = Rkj。
(2)當(dāng)網(wǎng)孔電流均取順時(shí)針或逆時(shí)針方向時(shí),Rjk均為負(fù)。
解2:
為了減少計(jì)算量,可以只讓一個(gè)回路電流經(jīng)過R5支路如圖所示。此時(shí)回路方程為:
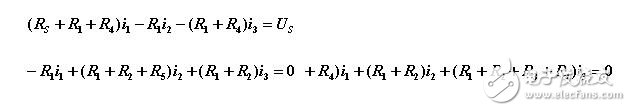
從以上方程中解出網(wǎng)孔電流2,則電流 ![]()
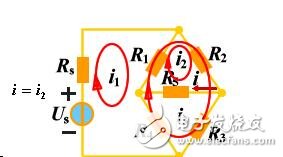
一個(gè)回路電流經(jīng)過R5支路
注:解法2的特點(diǎn)是計(jì)算量減少了,但互有電阻的識(shí)別難度加大,易遺漏互有電阻。本題也說明獨(dú)立回路的選取有多種方式,如何選取要根據(jù)所求解的問題具體分析。
 電子發(fā)燒友App
電子發(fā)燒友App




















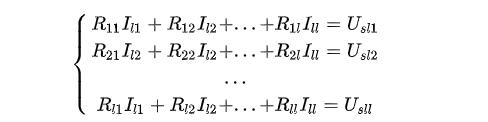











評(píng)論