什么是二進制計數器,二進制計數器原理是什么?
什么是二進制計數器,二進制計數器原理是什么?
計數器是數字系統中用得較多的基本邏輯器件。它不僅能記錄輸入時鐘脈沖的個數,還可以實現分頻、定時、產生節拍脈沖和脈沖序列等。例如,計算機中的時序發生器、分頻器、指令計數器等都要使用計數器。
計數器的種類很多。按時鐘脈沖輸入方式的不同,可分為同步計數器和異步計數器;按進位體制的不同,可分為二進制計數器和非二進制計數器;按計數過程中數字增減趨勢的不同,可分為加計數器、減計數器和可逆計數器。
二進制異步計數器:
1.二進制異步加計數器
電路結構
以三位二進制異步加法計數器為例,如圖8.4.1所示。該電路由3個上升沿觸發的D觸發器組成,具有以下特點:每個D觸發器輸入端接該觸發器Q 端信號,因而Q n+1=Q n,即各D觸發器均處于計數狀態;計數脈沖加到最低位觸發器的C端,每個觸發器的Q 端信號接到相鄰高位的C端。
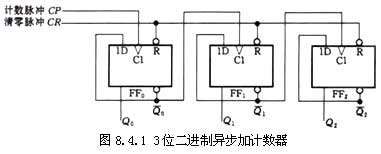
(2)原理分析:
假設各觸發器均處于0態,根據電路結構特點以及D觸發器工作特性,不難得到其狀態圖和時序圖,它們分別如圖8.4.2和圖8.4.3所示。其中虛線是考慮觸發器的傳輸延遲時間tpd后的波形。

由狀態圖可以清楚地看到,從初始狀態000(由清零脈沖所置)開始,每輸入一個計數脈沖,計數器的狀態按二進制遞增(加1),輸入第8個計數脈沖后,計數器又回到000狀態。因此它是23進制加計數器,也稱模八(M=8)加計數器。
從時序圖可以清楚地看到Q0,Q1,Q2的周期分別是計數脈沖(CP)周期的2倍,4倍、8倍,也就是說Q0,Q1,Q2,分別對CP波形進行了二分頻,四分頻,八分頻,因而計數器也可作為分頻器。
需要說明的是,由圖8.4.3中的虛線波形可知,在考慮各觸發器的傳輸延遲時間tpd時,對于一個n 位的二進制異步計數器來說,從一個計數脈沖(設為上升沿起作用)到來,到n 個觸發器都翻轉穩定,需要經歷的最長時間是ntpd ,為保證計數器的狀態能正確反應計數脈沖的個數,下一個計數脈沖(上升沿)必須在ntpd 后到來,因此計數脈沖的最小周期Tmin=ntpd 。
2.二進制異步減計數器:
圖8.4.4是3位二進制異步減計數器的邏輯圖和狀態圖。從初態000開始,在第一個計數脈沖作用后,觸發器FF0由0翻轉為1(Q0的借位信號),此上升沿使FF1也由0翻轉為1(Q1的借位信號),這個上升沿又使FF2 由0翻轉為1,即計數器由000變成了111狀態。在這一過程中,Q0向Q1進行了借位,Q1向Q2進行了借位。此后,每輸入1個計數脈沖,計數器的狀態按二進制遞減(減1)。輸入第8個計數脈沖后,計數器又回到000狀態,完成一次循環。因此,該計數器是23進制(模8)異步減計數器,它同樣具有分頻作用。

綜上所述,可對二進制異步計數器歸納出以下兩點:
(1)n位二進制異步計數器由n個處于計數工作狀態(對于D 觸發器,使Di=Qin;對于JK 觸發器,使Ji=Ki=1) 的觸發器組成。各觸發器之間的連接方式由加、減計數方式及觸發器的觸發方式決定。對于加計數器,若用上升沿觸發的觸發器組成,則應將低位觸發器的Q 端與相鄰高一位觸發器的時鐘脈沖輸入端相連(即進位信號應從觸發器的Q 端引出);若用下降沿觸發的觸發器組成,則應將低位觸發器的Q 端與相鄰高一位觸發器的時鐘脈沖輸入端連接。對于減計數器,各觸發器的連接方式則相反。
(2)在二進制異步計數器中,高位觸發器的狀態翻轉必須在低一位觸發器產生進位信號(加計數)或借位信號(減計數)之后才能實現。故又稱這種類型的計數器為串行計數器。也正因為如此,異步計數器的工作速度較低。
8.4.2 二進制同步計數器
為了提高計數速度,可采用同步計數器,其特點是,計數脈沖同時接于各位觸發器的時鐘脈沖輸入端,當計數脈沖到來時,各觸發器同時被觸發,應該翻轉的觸發器是同時翻轉的,沒有各級延遲時間的積累問題。同步計數器也可稱為并行計數器。
1.二進制同步加計數器
圖8.4.5是用JK觸發器(但已令J=K)組成的4位二進制(M=16)同步加計數器。
由圖可見,各位觸發器的時鐘脈沖輸入端接同一計數脈沖CP ,各觸發器的驅動方程分別為J0=K0=1,J1=K1=Q0、J2=K2=Q0Q1、 J3=K3=Q0Q1Q2 。
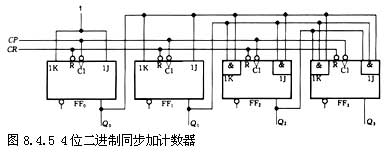
根據同步時序電路的分析方法,可得到該電路的狀態表,如表8.4.1所示。設從初態0000開始,因為J0=K0=1,所以每輸入一個計數脈沖CP,最低位觸發器FF0就翻轉一次,其他位的觸發器FFi僅在 Ji=Ki=Qi-1Qi-2……Q0=1的條件下,在CP 下降沿到來時才翻轉。
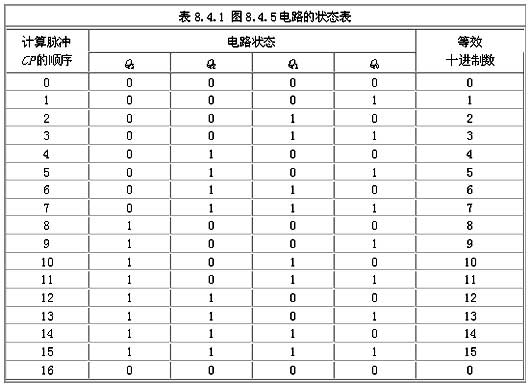
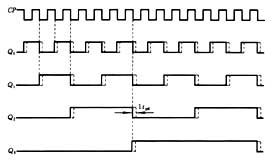
圖8.4.6是圖8.4.5電路的時序圖,其中虛線是考慮觸發器的傳輸延遲時間tpd 后的波形。由此圖可知,在同步計數器中,由于計數脈沖CP 同時作用于各個觸發器,所有觸發器的翻轉是同時進行的,都比計數脈沖CP 的作用時間滯后一個tpd ,因此其工作速度一般要比異步計數器高。
應當指出的是,同步計數器的電路結構較異步計數器復雜,需要增加一些輸入控制電路,因而其工作速度也要受這些控制電路的傳輸延遲時間的限制。如果將圖8.4.5電路中觸發器FF1、FF2和FF3的驅動信號分別改為
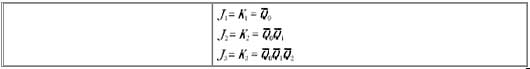
即可構成4位二進制同步減計數器.
2.二進制同步可逆計數器:
實際應用中,有時要求一個計數器即能作加計數又能作減計數。同時兼有加和減兩種計數功能的計數器稱為可逆計數器。
4位二進制同步可逆計數器如圖8.4.7所示,它是在前面介紹的4位二進制同步加和減計數器的基礎上,增加一控制電路構成的。由圖可知,各觸發器的驅動方程分別為
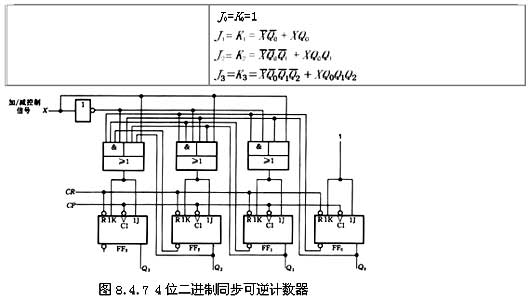
當加/減控制信號X=1時,FF1-FF3中的各J、K 端分別與低位各觸發器的Q 端接通,進行加計數;當X=0時,各J、K 端分別與低位各觸發器的Q 端接通,進行減計數,實現了可逆計數器的功能
由于雙穩態觸發器有“1“和”0“兩個狀態,所以一個觸發器可以表示移位二進制數。如果要表示n位二進制數,就得用n個觸發器。
??? 下表是四位二進制加法計數器得狀態表,用四個雙穩態觸發器,它們具有計數功能:
??? 1.異步二進制加法計數器
| 計數脈沖數 | 二進制數 | 十進制數 | |||
| Q3 | Q2 | Q1 | Q0 | ||
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 1 | 0 | 2 |
| 3 | 0 | 0 | 1 | 1 | 3 |
| 4 | 0 | 1 | 0 | 0 | 4 |
| 5 | 0 | 1 | 0 | 1 | 5 |
| 6 | 0 | 1 | 1 | 0 | 6 |
| 7 | 0 | 1 | 1 | 1 | 7 |
| 8 | 1 | 0 | 0 | 0 | 8 |
| 9 | 1 | 0 | 0 | 1 | 9 |
| 10 | 1 | 0 | 1 | 0 | 10 |
| 11 | 1 | 0 | 1 | 1 | 11 |
| 12 | 1 | 1 | 0 | 0 | 12 |
| 13 | 1 | 1 | 0 | 1 | 13 |
| 14 | 1 | 1 | 1 | 0 | 14 |
| 15 | 1 | 1 | 1 | 1 | 15 |
| 16 | 0 | 0 | 0 | 0 | 0 |
??? 由上表可見,每來一個計數脈沖,最低位觸發器翻轉一次;而高位觸發器是在相鄰得低位觸發器從“1“變位”0“進位時翻轉。因此,可用四個主從型JK觸發器來組成四位異步二進制加法計數器,如圖22.3.所示。每個觸發器的J,K端懸空,相當于”1“,故具有計數功能。觸發器的進位脈沖從Q端輸出送到相鄰高位觸發器的C端,這符合主從型觸發器在輸入正脈沖的下降沿觸發的特點。圖22.3.2是它的工作波形圖。由于計數脈沖不是同時加到各位觸發器的C端,而只加到最低位觸發器,其他各位觸發器則由相鄰低位觸發器輸出的進位脈沖來觸發,因此它們狀態的變化有先有后,是異步的,稱為異步加法計數器。
??? 2.同步二進制加法計數器
???? 如果計數器還是用四個主從型JK觸發器組成,根據上表可得出各位觸發器的J,K端的邏輯關系式:
???? ![]()
???? ![]()
???? ![]()
???? ![]()
??? 由上述邏輯關系式可得出上圖所示的四位同步二進制加法計數器的邏輯圖。由于計數脈沖同時加到各位觸發器的C端,它們的狀態變換和計數脈沖同步。
非常好我支持^.^
(102) 21.3%
不好我反對
(378) 78.7%
相關閱讀:
- [電子說] STM32基礎知識:定時器的定時計數功能 2023-10-24
- [電子說] 脈沖定時器時間未到而在此觸發IN端則會重新計時是否正確?為什么? 2023-10-24
- [電子說] 請問異步FIFO的溢出操作時怎么樣判斷的? 2023-10-18
- [電子說] 嵌入式狀態機編程-QP狀態機框架基本知識介紹 2023-10-18
- [電子說] 什么是奇校驗和偶校驗?常見的奇偶校驗方式有哪些? 2023-10-17
- [電子說] IPv6地址如何劃分?這篇文章看完必懂! 2023-10-17
- [電子說] 數字電路中的計數器詳解 2023-10-17
- [電子說] 開放二進制翻譯聯盟,推動RISC-V實現跨架構應用運行 2023-10-17
( 發表人:admin )
