越是基本而關鍵的概念，越容易誤解滿天飛。像“可靠性”這種被不斷提及的名詞，如果仔細分辨就會發現里面充斥著各種似是而非的誤解和誤用。

一、持久性、可用性，傻傻分不清

我們一般所說的“可靠性”，其實是個比較模糊的概念，里面包含持久性和可用性兩個層面的意思。

打開AWS S3的介紹頁面（https://aws.amazon.com/cn/s3/details/），會看到這樣一句話：

“設計目的是在指定年度內為對象提供99.999999999% 的持久性和 99.99% 的可用性。”

這是一句很嚴謹的表述，如果你已經完全理解這句話的意思，就可以直接跳過本節往下看了。

但如果你似懂非懂還看著“持久性”這個詞不懷好意的怪笑，說明你不僅歪腦筋太多，而且當初數據庫基礎知識沒學好，這里的持久性概念，就是從數據庫的持久性概念借鑒來的。

持久性和可用性的含義，可以用下面這個圖來理解。

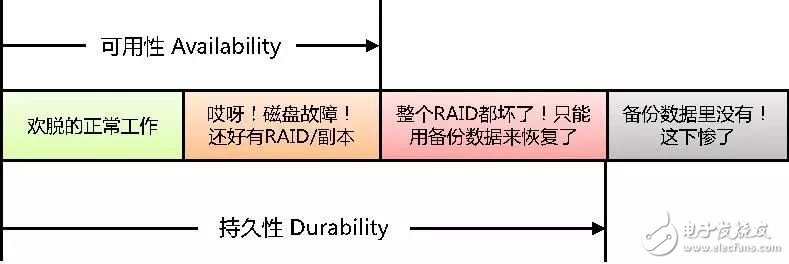
這個圖只是簡要的說明含義，實際系統中還有集群、容災等等各種環節，為了不分散焦點，無關本質的部分都略去不提。

簡單的說，數據可訪問就叫available——可用（這個翻譯很靠譜）。而數據暫時不可訪問，但是過段時間費些力氣能找回來，這樣的狀態已經不能叫available，但仍然屬于durable——持久（這個翻譯實在讓人抓狂，可是既然從早年數據庫領域就一直這么翻譯，現在已經成了固定用法，手動無奈）。只有數據徹底丟失，永遠找不回來的狀態，才超出durable的范圍。

可見，持久性比可用性更基礎，前者是后者的必要非充分條件。從數值描述上，持久性≥可用性。

另外，討論持久性和可用性時，需要限定邊界條件。孤立系統給出的量化指標，僅指裸奔時的表現，實際使用中還要看外面披著什么樣的使用方式。

比如AWS S3給出的那個承諾，持久性99.999999999%的含義，就是每年100000000000個對象中，可能會有1個對象丟失。這當然是個貌似很可靠的系統，假設你租來1百億個對象，想等著看到其中一個崩潰的話，可能要等10年。

可是且慢，Stack Overflow上曾有個頑皮的提問者，他說如果往AWS S3上存1百億個文件，是不是10年之內就可能出現文件丟失？

鑒于S3主要用于長期數據歸檔，且在全球范圍用量之大，這個提問并不算抬杠。也就是說，霸道如AWS的11個9持久性，也未必足以支撐浩瀚的數據海洋直到地老天荒。

當然這個提問者并不是真的發現了什么死結，后面的應答者很快就告訴他，只要在存文件的時候，增加一些校驗容錯機制，就能在S3對象崩掉幾個的時候仍然保持文件的完好無損。

對搞存儲的人來說，這個道理實在太容易理解了，就是在S3對象上做RAID嘛。這個模式可以推而廣之，但凡你對某個系統裸奔的可靠性不夠放心，就想辦法在上面“做RAID”即可，只要小心別用RAID-0擴大故障概率就行。

總之，理解了持久性、可用性這些概念，并知道哪些受限于設備，哪些掌握于自身，以后再看到那種一味強調幾個9的產品宣傳，就不至于被輕易忽悠。

二、時間邊界和故障規律

一般談論持久性和可用性，都需要或隱或顯的在百分數前面加個“年度”的限定。比如99%可用性，是指每年宕機時間不超過3.65天，即87.6小時。而99.9%可用性，就意味著每年宕機時間不超過8.76小時。人們常提的5個9高可用，即99.999%可用性，折算下來每年宕機時間才僅有5.256分鐘。

那么一個霸氣側漏的每年5個9高可用系統，在100年時間里可用性是多少呢？理論上似乎是仍然足夠威風的99.9%可用性（精確計算結果應該是略小于99.90005%一丟丟），可是這顯然不太合常理。再強壯的硅基物種，在機房里負重蹲上100年，肯定早就徹底散架了。

所以持久性和可用性的另外一個隱含限定——正常壽命之內。可惜對硅基物種正常壽命的界定，也是真假信息混雜。

以最常出故障的磁盤設備為例，每個磁盤型號都有一個MTBF指標（Mean Time Between Failure，平均無故障時間），來聲明其可靠性。具體的定義和解釋隨處可以查到，我就不廢話多說。

關于MTBF，我只有一句奉勸：

不要相信！不要相信！永遠不要相信！重要的事情說三遍。

作為標榜品質的主要規格指標，磁盤的MTBF已經徹底淪落純粹吹牛手段，數值從起初還算靠譜的幾萬小時，一路漲到極度夸張的幾百萬小時。

100萬小時=114年！

你要是真相信有磁盤可以用這么久的話，本文后面的部分也就沒必要看下去了。

所幸早在2007年，谷歌的幾位大牛就氣不過這種不負責任的胡說，用一篇名為《Failure Trends in a Large Disk Drive Population》的論文怒懟硬盤廠商。論文中統計了數萬顆磁盤的運維數據，發現實際環境中企業級磁盤和桌面級磁盤的故障概率非常接近，幾乎無差別。而廠商卻對兩種磁盤的MTBF標注差別明顯，甚至相差數倍。無論哪種盤，實際統計的AFR（年故障率）都遠高于MTBF的推算值若干數量級。

順便提一句，論文還指出磁盤實際AFR會高達3~8%，遠高于磁盤廠商根據返廠報修統計的0.4~1.2%每年。這中間的差額部分去了哪里，大家自行腦補吧。人艱不拆。

谷歌論文的統計對象，都是使用5年以內的磁盤。磁盤的原廠保修期一般也都是5年。這個壽命選擇來源于磁盤故障率的U型分布規律。

一般磁盤故障多發生在新上線3個月之內，或是臨近保修期結束前后，中間的階段相對比較消停。

新磁盤的故障，主要由制造過程的疏漏或錯誤造成。比如盤體密封不嚴，就會在上線工作后很快發生故障。這屬于硅基物種個體的先天缺陷導致的夭折。這類問題在經過一段時間負載后，很快就會全部暴露。

接下來，系統中剩下一群健康的青壯年磁盤，故障率自然會明顯下降。然而磁盤這種每分鐘要旋轉成千上萬次的物種，在歡脫的旋轉了幾萬小時之后，還是會鐵杵磨成繡花針，最終迎來衰老期。于是故障率又開始上升。

需要注意，磁盤的損耗速度與工作環境和負載有密切的關系。在悠閑舒適的環境中可以順利撐到5年的磁盤，換到負載繁重殘酷壓榨的環境里肯定要折壽。

從谷歌那篇論文里可以窺見，谷歌的數據中心一定是個殘酷壓榨磁盤的血汗工廠，因為里面的磁盤在2年左右就已經開始明顯衰老。貼張論文中的圖示，大家感受一下。

說了這么多，總結起來就是硅基物種跟我們這些碳基物種一樣，都有生老病死的全過程。討論硅基物種的可靠性，就如同討論我們碳基物種的健康度，不僅個體間有差異，而且每個個體的情況也隨時間和環境的變化而變化。

三、可靠性的量化計算

對可靠性的量化計算，絕對是各種錯誤頻生的重災區。如果在網上搜索這方面的計算方法，包括來自產品廠商、大學研究機構、社區論壇自由人士等各方面給出的種種計算公式和計算邏輯，80%以上都存在錯誤和漏洞。

有實際運維經驗的機房背鍋俠們，見多了這種貌似有理實則計算結果很扯的各類公式之后，都會對系統可靠性心生迷之不可知，繼而拋棄多年的理工科信念，毅然走上迷信的道路。

為了挽救迷途的運維工程師，重振數理化的威望，我們還是認真看看可靠性到底怎么計算吧。

對于簡單系統，相信理工科畢業的同學們還不至于被搞暈。

比如串行系統（RAID-0就是典型）中，所有單元都健康時系統才健康，所以系統健康概率計算方法就是每個單元健康概率的相乘。類似的，并行系統（比如多副本）中，所有單元都故障時系統才故障，所以系統故障概率是所有單元故障概率的乘積，而健康概率就是1減去故障概率。

腦力熱身完成，我們現在考慮一個稍微復雜一些的系統。

假設一個n節點的分布式存儲系統，每個節點中m顆磁盤，系統中采用k副本數據保護，副本都是跨節點保存，每顆磁盤的健康概率是p，那么系統的總體健康概率是多少呢？

好吧，我承認，難度跳躍比較大，從熱身的基本概念直接跳到這里的確少了些鋪墊。那我們至少先琢磨一下，這些條件是否足夠推算出系統的可靠性，是否還需要增加哪些限定條件。

敲黑板！重點來了！

大部分網上的錯誤計算邏輯，其實都忽視了同一個因素——時間。

我在前一節提到過，如果一個單元或系統，在1年里的可靠性是99%，那么它在1天里的可靠性應該是99.997%，在10年里的可靠性又變成了90.4%。不統一時間跨度之前，不能量化計算。就像各種理財產品一樣，有的3個月賺2%，有的5年賺20%，要想比較哪個收益率高，首先必須把收益換算為年化收益率。可靠性也是一樣，在計算過程中，時刻需要注意“年化”處理。

我們再看剛剛題目中n、m、k、p幾個條件，除了p需要考慮年化之外，似乎其他幾個條件都跟時間沒有直接關系，我們應該可以開始推算了。

先別急，我們還需要考慮另外一個問題——什么狀態是故障狀態？

一定會有人不假思索脫口而出，多盤同時故障，多到k副本全都壞了，就是故障狀態。可是，哪里有嚴格意義的“同時”呢？所有磁盤在同一月或同一年里全都壞過一遍，算不算“同時”呢？

我相信大多數明白人嘴里這么說的時候，心里想的其實就是多盤故障的時間點過于密集，以至于k副本全壞光之前，都來不及修復出一份好數據。這才是我們常說的“多盤同時故障”實際所指的真實含義。

基于這樣的認識，我們知道在判定系統是否故障時，其實隱含著一個時間因素——數據修復所需要的時間窗口，也稱為降級（Downgrade）時間窗口。

這個時間窗口是從健康狀態下第一顆磁盤故障算起，直到修復回健康狀態為止。其中一般包含備件更換時間t和數據重建時間τ，總降級窗口為t+τ。

現在的很多分布式存儲為了縮短這個降級窗口，可以不等更換壞盤，直接在現有空閑空間進行重建。這種情況下t=0。數據修復重建無論如何都需要時間開銷，所以τ總不會為零。

我們現在知道剛才那個系統中，必須再附加t和τ兩個因素，才能進行可靠性計算。

到此鋪墊結束，公式出場。系統年化健康概率H的計算公式如下：

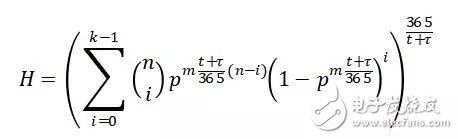
公式中t和τ的單位為天。

我還得承認，推演這個公式的過程中，沒有考慮故障的U型分布，而是簡單的用平均分布代替。至于原因嘛，我當然不會承認自己懶，也不會賣萌說等著大家來完善云云。我只是覺得未來的海量系統不會再像現在這樣分批次規劃建設，而是滾動式持續建設。那樣的話，系統中不同批次的設備混在一起，各年齡段都有，這個U型分布問題也就自然會被熨平。

暫時懶（kan）得（bu）看（dong）公式的同學也不要發飆，我列這個公式出來主要是想證明理工科信念還是要堅持，不能因為網上哪些邏輯有漏洞的錯誤就顛覆輕易放棄自己的信仰。只要考慮的因素周全一些，即便復雜系統里，也可以量化計算健康概率。

有興趣的同學可以試試用這個公式描畫一下H（n）、H（m）、H（t+τ）曲線，看看各個變量如何影響系統健康概率H的變化。相信你會有很多符合實際經驗，又頗感新鮮意外的感受。

我自己也做了一些延伸的變量曲線圖，這里就不貼出來了。有緣的話，等到4月14日深圳GOPS大會上跟大家分享。

這次GOPS大會上，我還要介紹一項徹底推翻可靠性構筑邏輯的新技術——磁盤故障預測。沒地方打廣告，就只能借自己的文章廣告一下了。