題目描述
給出 n 代表生成括號的對數(shù),請你寫出一個函數(shù),使其能夠生成所有可能的并且有效的括號組合。
例如,給出 n = 3,生成結(jié)果為:
[ "((()))", "(()())", "(())()", "()(())", "()()()" ] 題目解析
方法一:回溯算法(深度優(yōu)先遍歷)
如果完成一件事情有很多種方法,并且每一種方法分成若干步驟,那多半就可以使用“回溯”算法完成。
“回溯”算法的基本思想是“嘗試搜索”,一條路如果走不通(不能得到想要的結(jié)果),就回到上一個“路口”,嘗試走另一條路。
因此,“回溯”算法的時間復雜度一般不低。如果能提前分析出,走這一條路并不能得到想要的結(jié)果,可以跳過這個分支,這一步操作叫“剪枝”。
做“回溯”算法問題的基本套路是:
1、使用題目中給出的示例,畫樹形結(jié)構(gòu)圖,以便分析出遞歸結(jié)構(gòu);
一般來說,樹形圖不用畫完,就能夠分析出遞歸結(jié)構(gòu)和解題思路。
2、分析一個結(jié)點可以產(chǎn)生枝葉的條件、遞歸到哪里終止、是否可以剪枝、符合題意的結(jié)果在什么地方出現(xiàn)(可能在葉子結(jié)點,也可能在中間的結(jié)點);
3、完成以上兩步以后,就要編寫代碼實現(xiàn)上述分析的過程,使用代碼在畫出的樹形結(jié)構(gòu)上搜索符合題意的結(jié)果。
在樹形結(jié)構(gòu)上搜索結(jié)果集,使用的方法是執(zhí)行一次“深度優(yōu)先遍歷”。在遍歷的過程中,可能需要使用“狀態(tài)變量”。
(“廣度優(yōu)先遍歷”當然也是可以的,請參考方法二。)
我們以 n = 2 為例,畫樹形結(jié)構(gòu)圖。
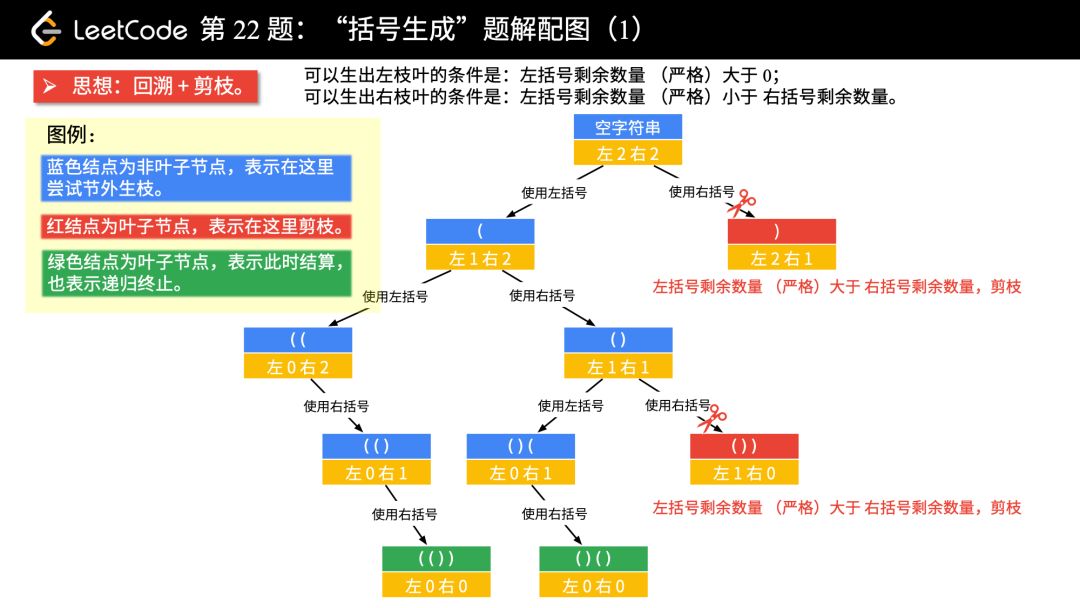
題解配圖(1)
畫圖以后,可以分析出的結(jié)論:
左右都有可以使用的括號數(shù)量,即嚴格大于 0 的時候,才產(chǎn)生分支;
左邊不受右邊的限制,它只受自己的約束;
右邊除了自己的限制以外,還收到左邊的限制,即:右邊剩余可以使用的括號數(shù)量一定得在嚴格大于左邊剩余的數(shù)量的時候,才可以“節(jié)外生枝”;
在左邊和右邊剩余的括號數(shù)都等于 0 的時候結(jié)算。
參考代碼如下:
publicclassSolution{ publicList
如果我們不用減法,使用加法,即 left 表示“左括號還有幾個沒有用掉”,right 表示“右括號還有幾個沒有用掉”,可以畫出另一棵遞歸樹。
題解配圖(2)
參考代碼如下:
publicclassSolution{ //方法 2:用加法 publicList
方法二:廣度優(yōu)先遍歷
還是上面的題解配圖(1),使用廣度優(yōu)先遍歷,結(jié)果集都在最后一層,即葉子結(jié)點處得到所有的結(jié)果集,編寫代碼如下。
publicclassSolution{ classNode{ /** *當前得到的字符串 */ privateStringres; /** *剩余左括號數(shù)量 */ privateintleft; /** *剩余右括號數(shù)量 */ privateintright; publicNode(Stringres,intleft,intright){ this.res=res; this.left=left; this.right=right; } @Override publicStringtoString(){ return"Node{"+ "res='"+res+'''+ ",left="+left+ ",right="+right+ '}'; } } publicList
方法三:動態(tài)規(guī)劃
第 1 步:定義狀態(tài) dp[i]
使用 i 對括號能夠生成的組合。
注意:每一個狀態(tài)都是列表的形式。
第 2 步:狀態(tài)轉(zhuǎn)移方程:
i 對括號的一個組合,在 i - 1 對括號的基礎上得到;
i 對括號的一個組合,一定以左括號 "(" 開始(不一定以 ")" 結(jié)尾),為此,我們可以枚舉右括號 ")" 的位置,得到所有的組合;
枚舉的方式就是枚舉左括號 "(" 和右括號 ")" 中間可能的合法的括號對數(shù),而剩下的合法的括號對數(shù)在與第一個左括號 "(" 配對的右括號 ")" 的后面,這就用到了以前的狀態(tài)。
狀態(tài)轉(zhuǎn)移方程是:
dp[i] = "(" + dp[可能的括號對數(shù)] + ")" + dp[剩下的括號對數(shù)]
“可能的括號對數(shù)” 與 “剩下的括號對數(shù)” 之和得為 i,故“可能的括號對數(shù)” j 可以從 0 開始,最多不能超過 i, 即 i - 1;
“剩下的括號對數(shù)” + j = i - 1,故 “剩下的括號對數(shù)” = i - j - 1。
整理得:
dp[i] = "(" + dp[j] + ")" + dp[i- j - 1] , j = 0, 1, ..., i - 1
第 3 步:思考初始狀態(tài)和輸出:
初始狀態(tài):因為我們需要 0 對括號這種狀態(tài),因此狀態(tài)數(shù)組 dp 從 0 開始,0 個括號當然就是 [""]。
1、自底向上:從小規(guī)模問題開始,逐漸得到大規(guī)模問題的解集;
2、無后效性:后面的結(jié)果的得到,不會影響到前面的結(jié)果。
publicclassSolution{ //把結(jié)果集保存在動態(tài)規(guī)劃的數(shù)組里 publicList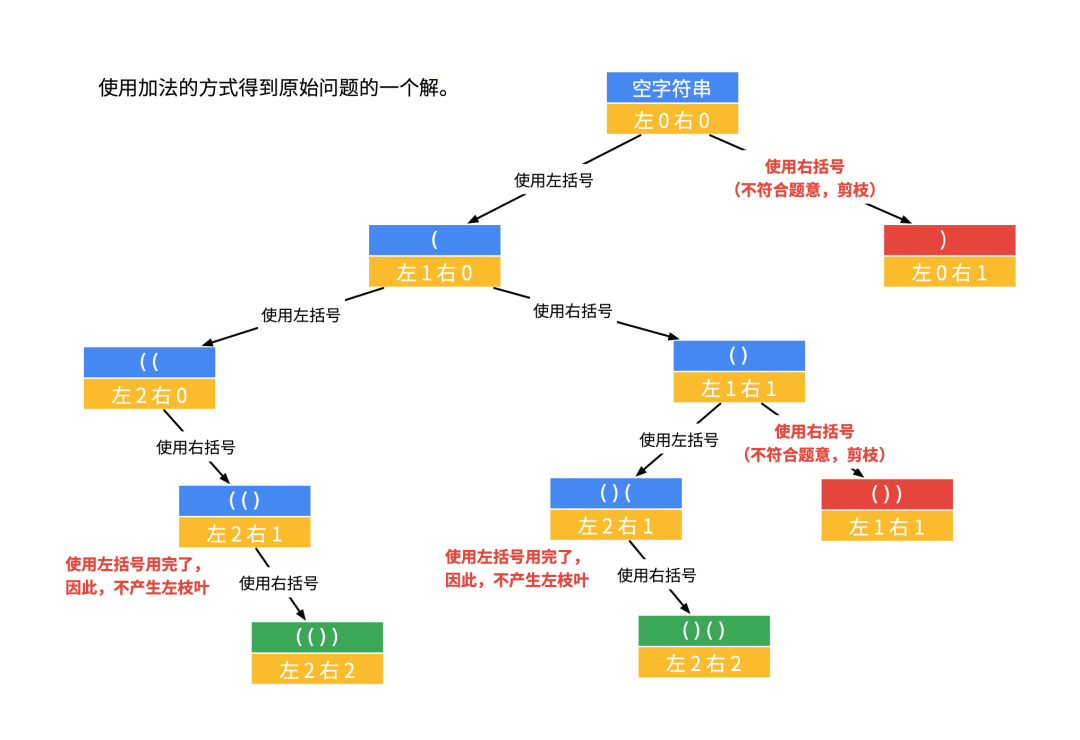
輸出:dp[n] 。
這個方法暫且就叫它動態(tài)規(guī)劃,這么用也是很神奇的,它有下面兩個特點:
-
算法
+關(guān)注
關(guān)注
23文章
4710瀏覽量
95392 -
遞歸
+關(guān)注
關(guān)注
0文章
29瀏覽量
9186
原文標題:超詳細!詳解一道高頻算法題:括號生成
文章出處:【微信號:TheAlgorithm,微信公眾號:算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
聚徽制造業(yè)專屬工業(yè)觸摸屏:精準控制每一道工序,提升生產(chǎn)精度
超高頻四通道RFID讀寫器在倉儲物流中的應用
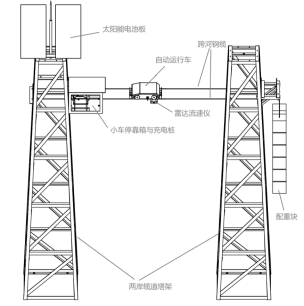
水文監(jiān)測中的雙軌纜道小車和鉛魚纜道小車
成品電池綜合測試儀:電池品質(zhì)的最后一道把關(guān)人
SVPWM的原理及法則推導和控制算法詳解
EDA2俠客島難題挑戰(zhàn)·2025已正式開啟
富士通如何解鎖生成式AI紅利 從人才進化到業(yè)務賦能
硬件工程師面試常考的一道題,講講運算放大器的增益帶寬積






 詳解一道高頻算法題:括號生成
詳解一道高頻算法題:括號生成












評論