“傅里葉”這個名字,我相信對很多人來說并不陌生。尤其是理工科的童鞋,對這三個字應該是如雷貫耳。
一直以來,在我們的大學專業課本中,“傅里葉”都保持著極高的出鏡率。圍繞這三個字的一系列名詞,例如傅里葉變換、傅里葉積分、傅里葉級數,傅里葉分析等等,曾經讓無數人苦不堪言、生不如死,甚至形成了長期的心理陰影。

然后,作為一位250年前的古人,至今還能在我們的教材中擁有如此重要的地位,也足以說明他的實力。
傅里葉究竟是一個什么樣的人?他經歷了一個怎樣的人生?他的這些成就,究竟是如何取得的?
今天的文章,我們就來找尋一下答案——
傅里葉(也有譯作傅立葉),全名是讓·巴普蒂斯·約瑟夫·傅里葉(Baron Jean Baptiste Joseph Fourier),法國著名數學家、物理學家。
傅里葉
1768年3月21日,他生于法國中部奧塞爾的一個平民家庭,他的父親是一個裁縫,母親是一個普通的家庭婦女。
傅里葉的童年并不算幸福。9歲時,雙親亡故,他變成一個孤兒,被當地的一個主教收養。
1780年,他被教會送入鎮上的軍校就讀,表現出對數學的特殊愛好。他曾經希望參加炮兵或工程兵,但因家庭地位低貧而遭到拒絕。
后來,他希望到巴黎更優越的環境中去從事數學研究。可是,法國大革命爆發,中斷了他的計劃。無奈之下,他于1789年回到家鄉奧塞爾的母校執教。
在大革命期間,傅里葉以熱心地方事務而知名,而且是一個非常有正義感的人。他替當時恐怖行為的受害者申辯,結果因此被捕入獄。出獄后,他短暫就讀于巴黎師范學校,再次表現出驚人的數學才華。
1795年,當巴黎綜合工科學校成立時,傅里葉被任命為助教,協助J.L.Lagrange(也就是拉格朗日,相信大家一定不會陌生)和G.Monge(蒙日,也是超級大牛),從事數學教學工作。這一年,他再次因政治原因被捕,后經同事營救獲釋。
拉格朗日 蒙日
1798年,蒙日選派他跟隨拿破侖遠征埃及。
在埃及開羅,他擔任埃及研究院的秘書,并從事許多外交活動。這一期間,他仍不斷地進行個人的業余研究,即數學物理方面的研究。
1801年,傅里葉回到法國。他希望繼續執教于巴黎綜合工科學校,但因拿破侖賞識他的行政才能,任命他為伊澤爾地區首府格勒諾布爾的高級官員。
由于政聲卓著,1808年,拿破侖授予他男爵稱號。
此后,幾經宦海浮沉,1815年,傅里葉終于在拿破侖百日王朝的尾期辭去爵位和官職,毅然返回巴黎以圖全力投入學術研究。但是,失業、貧困以及政治名聲的落潮,使得傅里葉進入了一生中最艱難的時期。
好在昔日同事和學生對他施以援手,為他謀得統計局主管之職,才算維持住了生活。統計局的工作并不繁重,傅里葉得以繼續從事研究。
1816年,傅里葉被提名為法國科學院的成員。一開始,路易十八因為懷疑他與拿破侖的關系,拒絕了他的提名。后來,事情得到澄清,傅里葉于1817年就職科學院,其聲譽隨之迅速上升。
傅里葉的任職得到了當時年事已高的 P.S.M.de Laplace(也就是拉普拉斯)的支持,卻不斷受到 S.D.Poisson(泊松)的反對。事實上,后來兩人之間的恩恩怨怨一直就沒停歇過。
拉普拉斯 泊松
1822年,傅里葉被選為科學院的終身秘書,這是極有權力的職位。
1827年,他又被選為法蘭西學院院士,還被英國皇家學會選為外國會員。此時,他的個人榮譽達到了巔峰。
傅里葉一生為人正直,他曾對許多年輕的數學家和科學家給予無私的支持和真摯的鼓勵,從而得到他們的忠誠愛戴,并成為他們的至交好友。
在他幫助過的科學家中,有知名的 H.C.奧斯特(Oersted)、P.G.狄利克雷(Dirichlet)、N.H.阿貝爾(Abel)和 J.C.F.斯圖姆(Sturm)等人。
有一件令人遺憾的事,就是傅里葉收到伽羅瓦(Galois)的關于群論的論文時,他已病情嚴重而未閱,以致論文手稿失去下落。
傅里葉極度癡迷熱學,他甚至認為熱能包治百病。于是,在一個夏天,他關上了家中的門窗,穿上厚厚的衣服,坐在火爐邊,結果,他被活活熱死了。。。死了。。。了。。。
1830年5月16日,傅里葉卒于法國巴黎。
我們回顧一下傅里葉的科學成就。
他的成就主要在于他對熱傳導問題的研究,以及他為推進這一方面的研究所引入的數學方法。
早在遠征埃及時,他就對熱傳導問題產生了濃厚的興趣。后來在格勒諾布爾任職期間,他進行了大量的科學研究。
1807年,他向科學院呈交了一篇很長的論文,題為“熱的傳播”(Mémoire sur la propagation de la chaleur),內容是關于不連結的物質和特殊形狀的連續體(矩形的、環狀的、球狀的、柱狀的、棱柱形的)中的熱擴散(即熱傳導)問題。在論文的審閱人中,拉普拉斯、蒙日和 S.F.拉克魯瓦(Lacroix)都是贊成接受這篇論文的,但是拉格朗日提出了強烈的反對。
傅里葉在論文中運用正弦曲線來描述溫度分布,并提出一個很有爭議性的結論:任何連續周期信號可以由一組適當的正弦曲線組合而成。(這句話是不是很耳熟?高數課聽過,信號與系統課聽過,數字信號處理課也聽過。)
但是拉格朗日堅持認為傅里葉的方法無法表示帶有棱角的信號,如在方波中出現非連續變化斜率。(不懂?放心,我也不懂 )
最終,法國科學學會屈服于拉格朗日的威望,拒絕了傅里葉的工作。不過,在審查委員會給傅里葉的回信中,還是鼓勵他繼續鉆研,并將研究結果嚴密化。
究竟兩位大牛誰對誰錯呢?
正弦曲線無法組合成一個帶有棱角的信號,這句話拉格朗日是對的。但是,我們可以用正弦曲線來非常逼近地表示它,逼近到兩種表示方法不存在能量差別。基于此,傅里葉是對的。(某老師解釋的,我表示繼續不懂)
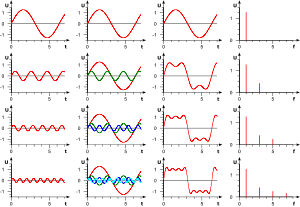
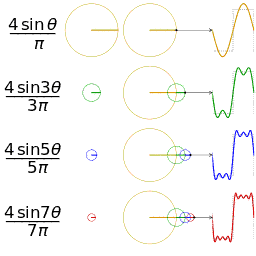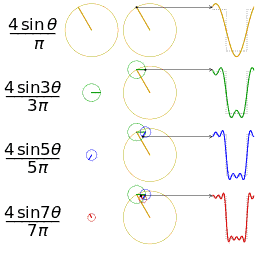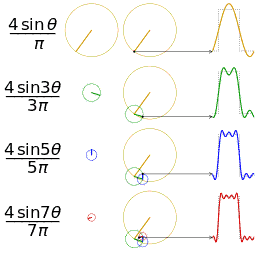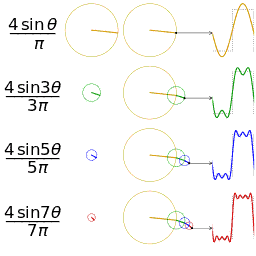
為了推動對熱擴散問題的研究,科學院于1810年懸賞征求論文。傅里葉對其1807年的文章加以修改,并再次提交,題目是“熱在固體中的運動理論”(Theorie du mouvement de chaleur clansles corps solides)。
這篇論文在競爭中獲勝,傅里葉獲得科學院頒發的獎金。但是評委——可能是由于拉格朗日的堅持——仍從文章的嚴格性和普遍性上給予了批評,以致這篇論文又未能正式發表。
這下子傅里葉徹底炸了。他認為這是一種無理的非難,他決心將這篇論文的數學部分擴充成為一本書(他本來還打算把物理部分出書,可惜后來沒有完成)。
1822年,傅立葉終于出版了專著《熱的解析理論》。
這部經典著作將歐拉、伯努利等人在一些特殊情形下應用的三角級數方法發展成內容豐富的一般理論,三角級數后來就以傅里葉的名字命名(傅里葉級數)。后來為了處理無窮區域的熱傳導問題又導出了“傅里葉積分”,這一切都極大地推動了偏微分方程邊值問題的研究。
然而傅里葉的工作意義遠不止此,它迫使人們對函數概念作修正、推廣,特別是引起了對不連續函數的探討;三角級數收斂性問題更刺激了集合論的誕生。
《熱的解析理論》影響了整個19世紀分析嚴格化的進程,在數學史,乃至科學史上公認是一部劃時代的經典性著作。
實際上,傅里葉變換遠不止數學和物理學上的價值,它幾乎存在于生活和科學的各個領域——研究不同的潛水器結構與水流的相互作用,試圖預測即將到來的地震,識別距離遙遠的星系的組成部分,尋找熱量大爆炸殘余物中的新物理成分,從x射線衍射模式揭示蛋白質的結構,為NASA分析數字信號,研究樂器的聲學原理,改進水循環的模型,尋找脈沖星(自轉的中子星),用核磁共振研究分子結構。甚至,傅里葉變換已經被用于通過破譯油畫中的化學物質,來識別假冒的杰克遜·波洛克繪畫。
-
傅里葉
+關注
關注
0文章
60瀏覽量
20798
原文標題:傅里葉的坎坷人生
文章出處:【微信號:mwrfnet,微信公眾號:微波射頻網】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
VirtualLab:光柵的優化與分析
VirtualLab 應用:薄元近似(TEA)與傅里葉模態法(FMM)的光柵建模
漫畫傅里葉解析-[日]涉谷道雄
VirtualLab Fusion應用:非近軸衍射分束器的設計與優化
VirtualLab Fusion應用:光波導應用中的光柵分析
VirtualLab Fusion案例:單分子顯微鏡高NA成像系統的建模
VirtualLab Fusion案例:高NA傅里葉單分子成像顯微鏡
低壓配電中產生的諧波應該如何治理?
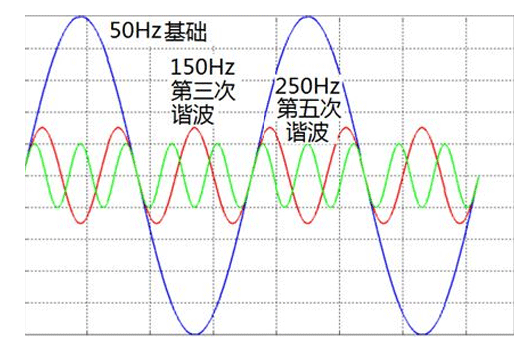





 傅里葉公式的由來
傅里葉公式的由來











評論