一.LDPC編碼介紹

1.為什么要用LDPC編碼，LDPC編碼相對其他編碼的好處

LDPC(低密度奇偶檢驗)碼是由稀疏校驗矩陣定義的線性分組碼，具有能夠逼近香農極限的優良特性，其描述簡單，具有較大的靈活性和較低的差錯誤碼特性，可實現并行操作，譯碼復雜度低，適合硬件實現，吞吐量大，極具高速譯碼的潛力，在碼長較長的情況下，仍然可以有效譯碼。

目前常用的信道編碼體制有BCH碼、RS碼、卷積碼、Turbo碼和LDPC碼等。其中BCH碼和RS碼都屬于線性分組碼的范疇，在較短和中等碼長下具有良好的糾錯性能；卷積碼在編碼過程中引入了寄存器，增加了碼元之間的相關性，在相同復雜度下可以獲得比線性分組碼更高的編碼增益；Turbo碼采用并行級聯遞歸的編碼器結構，其分量采用系統的卷積碼，能夠在長碼時逼近香農極限，同時譯碼復雜度也可以接收，但是它的譯碼復雜性仍然較大，且碼長較長時，由于交織器的存在具有較大的時延。

相比之下LPDC具有以下特性：

(1)譯碼的復雜度很低，運算量不會因為碼長的增加而急劇增加；

(2)采用迭代譯碼算法，可以實現并行操作，具有高速的譯碼能力；

(3)吞吐量大，從而改善系統的傳輸效率，并且便于硬件實現；

(4)譯碼復雜度與碼長成線性關系，克服了分組碼在長碼時所面臨的巨大譯碼計算復雜度的問題，使長編碼分組的應用成為可能。

二.LDPC編碼基礎
1. LDPC編碼的定義及矩陣表示
LDPC碼是一類具有稀疏矩陣的線性分組碼，在線性分組碼中，任意兩個碼字的和仍屬于這個分組碼，輸出的碼字只和輸入的信息位有關，即每個消息是獨立編碼的。

假設信源輸出一系列的二進制0和1，這些二進制塊分成固定長的消息塊，每個消息塊記作M，由k比特信息組成,其中M=[m0,m1,…m(k-1)]。然后根據一定的編碼方式產生一個n維向量，這個向量就叫做m的碼字，假設信息M對應的碼字位C，其中C=[c0,c1,…c(n-1)]，則可以找到k個線性無關的碼字g0,g1,…,g(k-1)，使得：

C= m0*g0+m1*g1+……+m(k-1)*g(k-1)

在C中，信息位不變，校驗位附加在信息為之后，寫成矩陣的形式就是：

C= M*G

G是k行n列的矩陣，又稱為生成矩陣。

另外，可以由n-k個n維線性無關向量h0,h1,…h(n-k-1)生成C⊥(表示與C對應的零空間)。因此對于任意的i，hi*CT=0寫成矩陣的形式就是H*CT=0。

H為(n-k)行n列的矩陣，通常被稱為校驗矩陣,用來判斷碼字是否合法。

2. LDPC碼的Tanner圖
LDPC編碼可以用Tanner圖來唯一確定，其和校驗矩陣是完全等價的。Tanner圖的頂點稱為節點，分為變量節點和校驗節點，每個變量節點與每個碼字比特相對應，它對應校驗矩陣的每一行，每個校驗節點與每個校驗方程相對應，它對應校驗矩陣的每一列，變量節點和校驗節點之間的連線稱為沿，也代表校驗矩陣中的1。例如校驗矩陣H如下：

圖1

用Tanner圖來表示H矩陣如下：

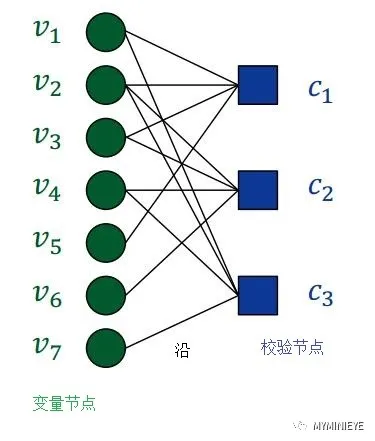
圖2

在上圖中，從節點v1出發，經節點c1,v2,c3，再回到v1，稱為一個環，環的周長為該環所包含的邊數，周長較短的環影響譯碼的性能，短環的存在會使得譯碼重復迭代，影響譯碼效率，使譯碼收斂速度變慢，在構造LDPC編碼時應盡量避免出現短環。

3.eIRA編碼算法
對LDPC碼的編碼可以采用線性分組碼的通用編碼方法，但通用編碼方法的編碼復雜度與碼長的平方成正比，編碼時延較大，實用性不強。eIRA(extended Irregular Repeat Accumulate，擴展的非規則重復累積碼)編碼算法，利用校驗矩陣的稀疏性進行有效編碼，使編碼復雜度與碼長成線性關系。

eIRA編碼算法需要構造具有如下形式的校驗矩陣

H=[H1 H2]

其中，H1是一個mXk維稀疏矩陣，H2是一個階梯狀下三角形矩陣，H2的形式如下：

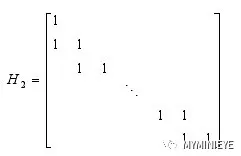
圖3

系統碼的生成矩陣形式為G=[I P]，其中I是單位矩陣 P=H1^TH2-T，H2^-T的形式為：

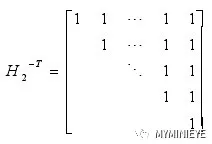
圖4

H2^-T可以看成一個累加器，也稱差分編碼器。因此，eIRA 編碼算法分兩步進行，首先將待編碼的信息矢量 m 乘以稀疏矩陣H1T，得到中間結果S，然后將中間結果S進行重復累加，得到校驗比特，最后將信息比特和校驗比特合并起來就得到最終的碼字。

三.LPDC編碼實現
1.LDPC編碼過程
LDPC編碼器的任務是將K個信息比特M=[m0,m1,…,m(k-1)]通過編碼得到(N-K)個奇偶校驗比特P=[p0,p1,…,p(n-k-1)]，最后得到的碼字是將信息比特與校驗比特合并，即得到碼長為N的碼字[i0,i1,…i(k-1),p0,p1,…,p(n-k-1)]。假設LDPC的碼長位16200，碼率為1/2，其中Nldpc = 16200,Kldpc =7200,Qldpc=25。

具體計算步驟如下：

(1)初始化p0=p1=p2=…=p(n-k-1)=0

(2)在表格中第一行指定的校驗位地址處累加信息位i0,如下圖所示，這一步的操作為編碼的信息矢量i乘以稀疏矩陣H1^T，一共有20行，即360*20 = 7200。

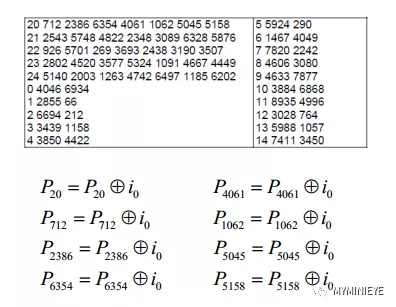
圖5

對于接下來的359個信息位，im,m=1,2,…,359。在{x+(m mod 360) * Qldpc } mod(Nldpc-Kldpc)指定的校驗位地址累加信息位im，其中x表示信息為i0對應的校驗位地址。

(3)對于信息i1，校驗位的地址需要根據 i0的地址來求，例如第一個校驗位地址,{20+(1 mod 360) * 25 } mod (9000) = 45，第二個校驗位{712+(1 mod 360) * 25} mod (9000) = 737，求出所有的校驗位地址，然后進行信息累加，如下：

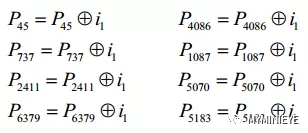
圖6

(4)對于第361個信息位i360，在表中的第二行指定了累加器對應的校驗位地址。和步驟3相同的處理方式，接下來的359個信息位對應的校驗位地址為{x+(m mod 360) * Qldpc} mod (Nldpc-Kldpc)，其中x表示i360對應的校驗位地址。

(5)以同樣的方式處理每一組信息位，給出每一組對應的校驗位地址。

(6)從i=1開始，按照下面的公式完成迭代計算

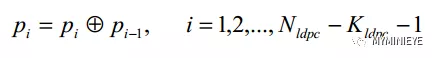
圖7

2.matlab實現
在matlab中，有專門的函數來實現ldpc編碼，但是在實現編碼之前，需要我們產生一個我們需要的校驗矩陣H。這里以Nldpc = 16200 ,碼率1/2為例，介紹校驗矩陣H的產生過程。

(1)按照上述LDPC編碼中提到的，把校驗位起始的地址存儲起來，用于計算

其他的校驗位。

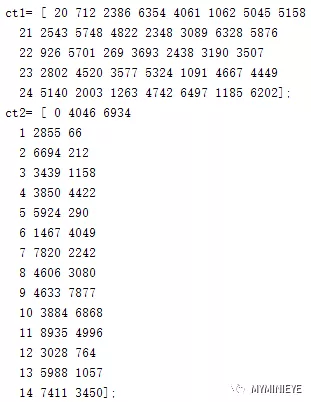
圖8

把數據分成兩組是因為數據的列數不一樣，把相同列數的歸到同一組里，這樣更方便計算。

(2)根據公式，第一行，計算剩余359個校驗位地址，其他行也做同樣的操作，如下代碼表示計算ct1所表示的校驗位，ct2校驗位的計算同ct1。

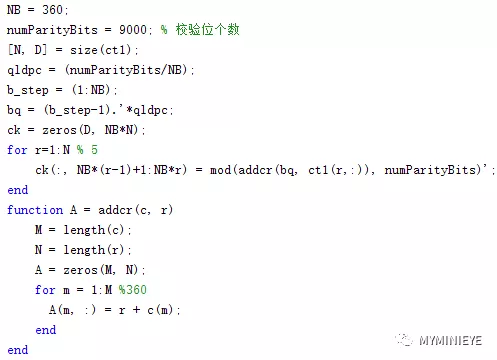
圖9

(3)計算完所有的校驗位之后，按照如下操作產生校驗矩陣

圖10

(4)用產生的校驗矩陣，計算LDPC編碼，這里使用comm.LDPCEncoder函數來實現，在較早的matlab版本中是fec.ldpcenc函數。

圖11

3.FPGA實現
FGPA不可能一次性存儲那么多的數據，并且也不現實，需要根據實時的計算產生校驗位。通過上述的分析可知，LDPC碼的編碼具有周期為360的并行結構，如果把長度為K的信息比特分成r=K/360組，長度為N-K的校驗比特分成s=(N-K)/360如下所示

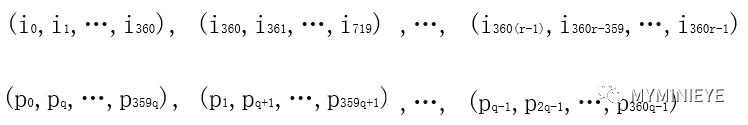
圖12

由每個信息比特對應的校驗比特公式pj=pj⊕im，其中j={x+(m mod 360)*q} mod(N-K)，x是第im個信息比特所對應的校驗比特地址。可知,每一組信息比特均參與了同一組校驗比特校驗的過程。

考慮到碼的周期性，我們可以同時進行M=360次并行處理，增加編碼效率，可以寫成以下迭代公式:

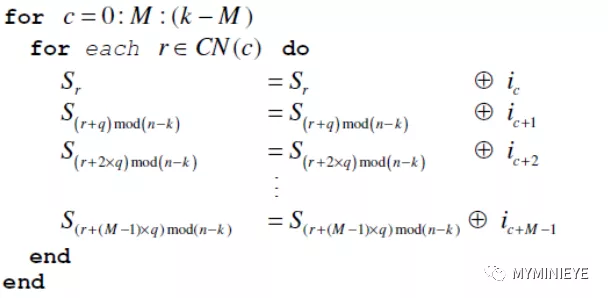
圖13

其中符號‘r’和‘c’表示校驗矩陣 H 的行和列，和信息節點連接的所有檢驗節點的集合定義為CN(c)。兩個迭代循環，每次計算M個信息位，按照下面的矩陣形式存儲Sr

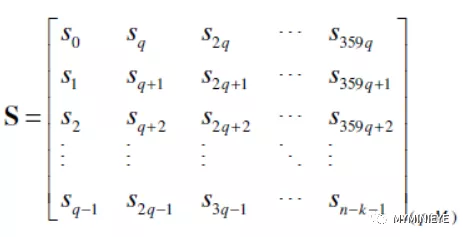
圖14

從公式中可以看到，并行更新的M個Sr處于矩陣的同一行，但是輸出的順序并不是我們想要的順序，不是從行的第一位到最后一位，因此需要對輸入的信息位做循環移位，以保證S矩陣的結構。

一旦得到Sr就可以得到pr

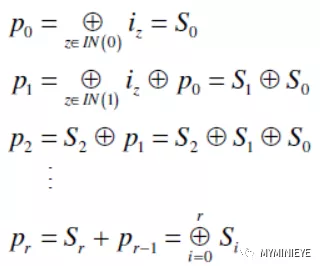
圖15

計算S矩陣所有列的累加和，可以的到下面的向量

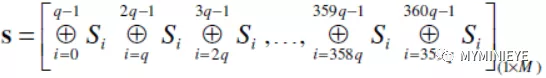
圖16

然后按照下面的公式計算s’

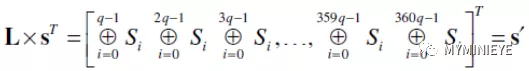
圖17

其中，L位MXM的下三角矩陣，然后將s’邏輯右移一位，得到

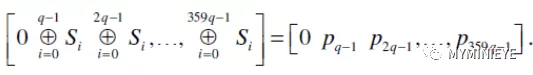
圖18

最后按照下面的公式，每次計算Mbit校驗位

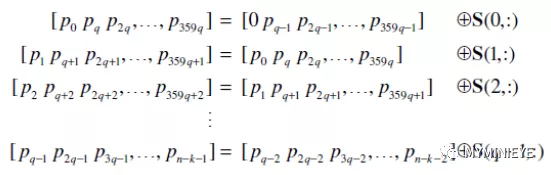
圖19

根據以上的公式推導，提出以下的實現結構，有三個主要部分組成：第一部分計算Sr的值，第二部分就算S矩陣中列的累加和，第三部分計算校驗位。編碼器的系統結構主要包括編碼配置模塊(Ldpc_contrl)，信息位分組計數模塊(data_recv)，基地址產生模塊(Bom_addr)，數據地址計算模塊(ADDER_GEN)，校驗位計算模塊(iterator)，整個系統結構如下圖所示：

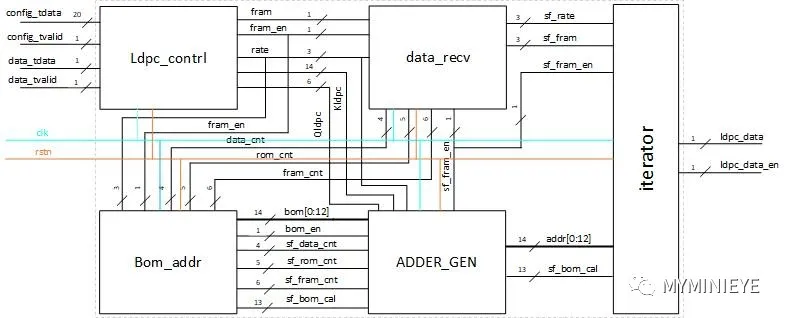
圖20

3.1編碼配置

在配置模塊中提供了1/4，1/2，3/5，2/3，3/4，4/5，5/6七種碼率，為了實現編碼方式的可配置，利用寄存器保存不同碼率下的參數，主要包括Qldpc,Kldpc，可以在整個系統結構中看到。首先檢測配置使能信號，然后加載配置數據，保存參數。其中fram和fram_en是輸入信息位和使能延遲輸出，考慮到最壞的情況下，配置信號和數據同時到來，需要先配置，才能進行數據的處理，所以對數據要延遲幾個時鐘周期。

3.2 信息位分組計數

模塊的主要作用是對輸入的信息比特進行序號標記，采用三個計數器，其中data_cnt為 0~14 表示15個數據 rom_cnt 為 0~23，24組表示共24*15=360個數據，0表示初始數據，fram_cnt，360bit的組數統計。如對應1/2碼率，輸入數據為7200bit，則數據可分為：20*360 = 20*15*24 =7200，下圖為信息位分組計數模塊主要信號的時序圖，延遲的是因為在計算校驗位地址的時候會花費時間，為了后邊計算校驗位時信息位能夠和校驗地址對齊。

圖21

3.3 基地址產生

基地址產生模塊根據輸入的碼率選擇存在rom中的基地址，選擇基地址的讀取位置由輸入的碼率和輸入序號共同確定，輸入碼率確定及地址的起始位置，序號fram_cnt確定基地址的偏移。以1/2碼率為例，rom中初始地址為63，當fram為0時表示第一行，讀取的基地址如下：

圖22

仿真時鐘周期為20ns，地址輸出相對信息位使能延遲了16個時鐘周期，其中移位輸出的計數器分別延時了兩個時鐘周期。延遲是為了在校驗位計算的時候，地址能夠和信息位對齊。

3.4 數據地址計算

地址計算模塊需要根據公式{x+(m mod360) * Qldpc } mod (Nldpc-Kldpc)，計算每個信息位所對應的校驗位。但是這個公式所用的取模以及乘法運算不適合在FPGA中運算，會占用很多的DSP資源，而且也是不必要的。以1/2碼率為例，可以轉化為如下的加減運算。

圖23

result = Amod B ，當A小于B時result等于A本身，當A大于B時result等于A-B，通過這個模塊計算出每個信息位所對應的的校驗位。

圖24

其中data_in_bom為初始地址，data_in_addr為計算的校驗位地址。

3.5校驗比特計算

校驗比特計算需要完成兩個部分，第一部分為信息位的輸出，第二部分為校驗位的輸出。因為在硬件中為實時處理。以1/2碼率為例，發送的16200bit碼字，包括7200bit信息位，9000bit校驗位，兩個部分分時段進行。系統采用13個并行度計算校驗位，其中的一個的時序如下：

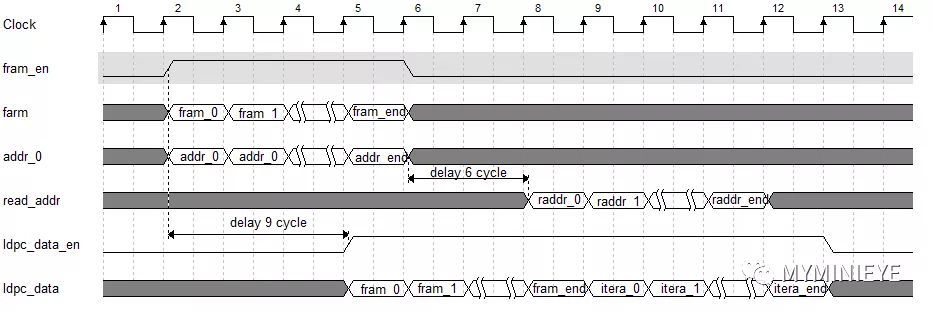
圖25

雙口ram設置為read first，數據相對于地址有三個時鐘的延遲。上述中所涉及的延遲均在調試中根據運算所需時鐘數進行的延遲。采用13個并行度計算校驗位，其中的一個的結構如下，addr_ena和addr_flag均由read_addr控制。

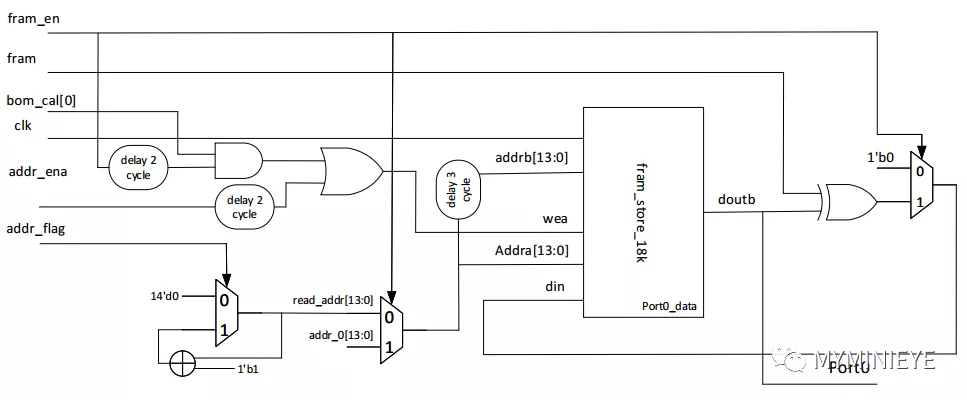
圖26

最后把每個13個并行度的數據相加，然后與上一位的值異或，得到最終的輸出。

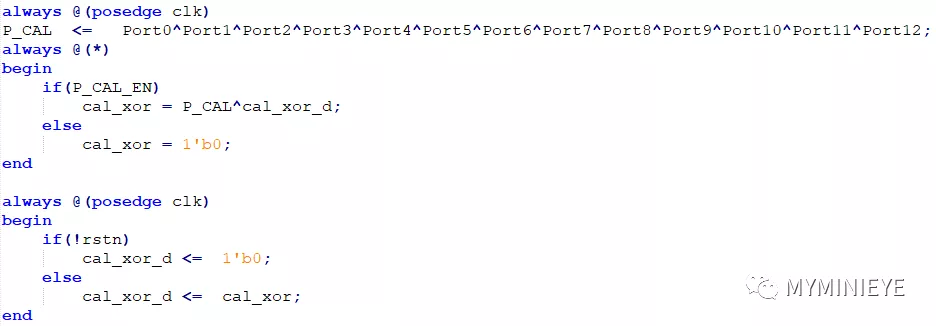
圖27

通過modelsim把結果輸出和matlab計算的結果進行比較，可以看到我們使用FPGA實現的結果和用matlab做出的結果是一樣的。

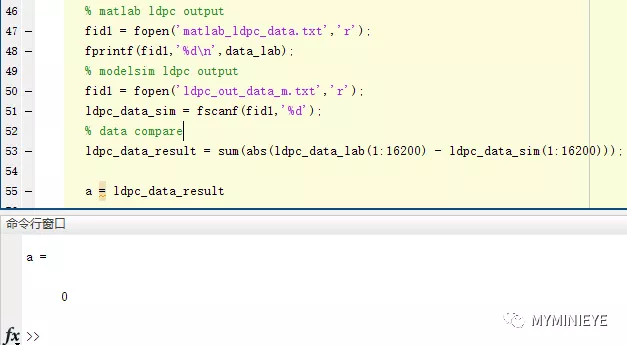
圖28