LeetCode初級算法--設計問題02:最小棧
一、引子
這是由LeetCode官方推出的的經典面試題目清單~
這個模塊對應的是探索的初級算法~旨在幫助入門算法。我們第一遍刷的是leetcode推薦的題目。
二、題目
設計一個支持 push,pop,top 操作,并能在常數時間內檢索到最小元素的棧。
- push(x) -- 將元素 x 推入棧中。
- pop() -- 刪除棧頂的元素。
- top() -- 獲取棧頂元素。
- getMin() -- 檢索棧中的最小元素。
示例:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
1、思路
第一種方法:
用列表模擬棧,push、pop、top和getMin分別對應list.append()、list.pop()、list[-1]和min()操作
第二種方法:
引入minStack列表存放最小值
2、編程實現
第一種方法:
class MinStack(object):
def __init__(self):
"""
initialize your data structure here.
"""
self.l = []
def push(self, x):
"""
:type x: int
:rtype: None
"""
if x is None:
pass
else:
self.l.append(x)
def pop(self):
"""
:rtype: None
"""
if self.l is None:
return 'error'
else:
self.l.pop(-1)
def top(self):
"""
:rtype: int
"""
if self.l is None:
return 'error'
else:
return self.l[-1]
def getMin(self):
"""
:rtype: int
"""
if self.l is None:
return 'error'
else:
return min(self.l)
# Your MinStack object will be instantiated and called as such:
# obj = MinStack()
# obj.push(x)
# obj.pop()
# param_3 = obj.top()
# param_4 = obj.getMin()
第二種方法:
class MinStack(object):
def __init__(self):
"""
initialize your data structure here.
"""
self.stack = [] #存放所有元素
self.minStack = []#存放每一次壓入數據時,棧中的最小值(如果壓入數據的值大于棧中的最小值就不需要重復壓入最小值,小于或者等于棧中最小值則需要壓入)
def push(self, x):
"""
:type x: int
:rtype: void
"""
self.stack.append(x)
if not self.minStack or self.minStack[-1]>=x:
self.minStack.append(x)
def pop(self): #移除棧頂元素時,判斷是否移除棧中最小值
"""
:rtype: void
"""
if self.minStack[-1]==self.stack[-1]:
del self.minStack[-1]
self.stack.pop()
def top(self):
"""
:rtype: int
"""
return self.stack[-1]
def getMin(self):
"""
:rtype: int
"""
return self.minStack[-1]
本文由博客一文多發平臺 OpenWrite 發布!
審核編輯 黃昊宇
聲明:本文內容及配圖由入駐作者撰寫或者入駐合作網站授權轉載。文章觀點僅代表作者本人,不代表電子發燒友網立場。文章及其配圖僅供工程師學習之用,如有內容侵權或者其他違規問題,請聯系本站處理。
舉報投訴
-
人工智能
+關注
關注
1804文章
48705瀏覽量
246473 -
機器學習
+關注
關注
66文章
8492瀏覽量
134087 -
深度學習
+關注
關注
73文章
5554瀏覽量
122479 -
leetcode
+關注
關注
0文章
20瀏覽量
2429
發布評論請先 登錄
相關推薦
熱點推薦
基于APM32F407如何制作I2C EEPROM(AT24C02型號)的MDK-Keil下載算法
基于APM32F407如何制作I2C EEPROM(AT24C02型號)的Keil下載算法,這樣在我們下載代碼時可以一鍵把數據燒錄到EEPROM中。
深入淺出解析低功耗藍牙協議棧
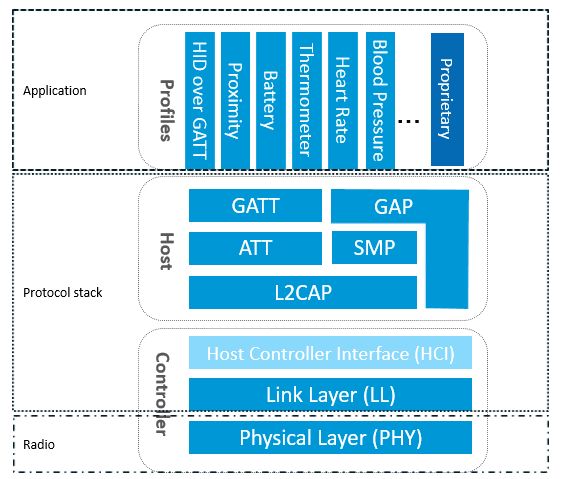
Bluetooth LE協議棧為什么要分層?怎么理解Bluetooth LE“連接”?如果Bluetooth LE協議只有ATT層沒有GATT層會發生什么? 一、協議棧框架 一般而言,我們把某個
自動駕駛全棧自研可行嗎?
隨著自動駕駛加速落地,全棧自研模式在高階智能駕駛技術領域逐漸成為共識,這種模式指的是整車廠從底層硬件、軟件算法到系統集成全面自主開發,而非依賴于第三方供應商或Tier 0.5模式(車企與供應商
曙光云開啟全棧智能時代
近日,“全棧可信 云中生智”曙光云戰略發布會召開。曙光云從首創“城市云”進化到實現“全棧智能云”,打造“云智、云安、云算、云數”四位一體能力體系,深度賦能千行百業數智化轉型升級。
常見的lvs負載均衡算法
常見的lvs負載均衡算法包括輪詢(RR)、加權輪詢(WRR)、最小連接(LC)、加權最小連接(WLC)、基于局部性的最少鏈接(LBLC)、帶復制的LBLC(LBLCR)、目標地址散列(DH)、源地址
λ-IO:存儲計算下的IO棧設計
動機和背景? ? 存儲計算存儲資源的充分利用。IO棧是管理存儲器的的基本組件,包括設備驅動、塊接口層、文件系統,目前一些用戶空間IO庫(如SPDK)有效降低了延遲,但是io棧仍然不可或缺。這是因為1

TPS62A02和TPS62A02A降壓轉換器評估模塊用戶指南
電子發燒友網站提供《TPS62A02和TPS62A02A降壓轉換器評估模塊用戶指南.pdf》資料免費下載
發表于 11-21 14:40
?0次下載

RVBacktrace RISC-V極簡棧回溯組件
RVBacktrace組件簡介一個極簡的RISC-V棧回溯組件。功能在需要的地方調用組件提供的唯一API,開始當前環境的棧回溯支持輸出addr2line需要的命令,使用addr2line進行棧回溯支持結合反匯編,棧回溯信息圖表化

Linux網絡協議棧的實現
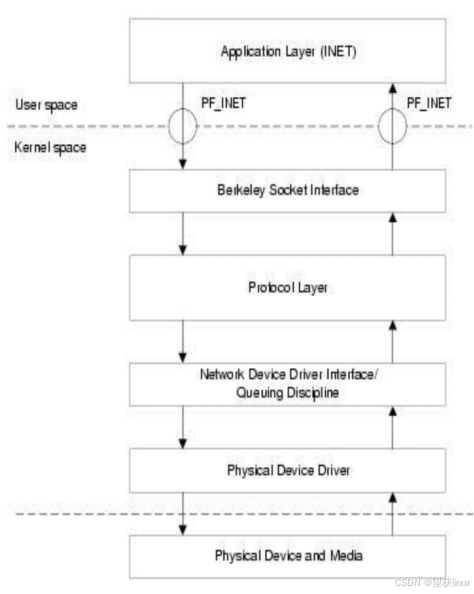
網絡協議棧是操作系統核心的一個重要組成部分,負責管理網絡通信中的數據包處理。在 Linux 操作系統中,網絡協議棧(Network Stack)負責實現 TCP/IP 協議簇,處理應用程序發起的網絡
神經網絡優化算法有哪些
神經網絡優化算法是深度學習領域中的核心技術之一,旨在通過調整網絡中的參數(如權重和偏差)來最小化損失函數,從而提高模型的性能和效率。本文將詳細探討神經網絡優化算法的基本原理、主要方法、變體、以及在實際應用中的注意事項和最新進展。





 LeetCode初級算法-設計問題02:最小棧
LeetCode初級算法-設計問題02:最小棧











評論