隨著深度學習的成功,基于圖神經網絡(GNN)的方法[8,12,30]已經證明了它們在分類節點標簽方面的有效性。大多數GNN模型采用消息傳遞策略[7]:每個節點從其鄰域聚合特征,然后將具有非線性激活的分層映射函數應用于聚合信息。這樣,GNN可以在其模型中利用圖結構和節點特征信息。然而,這些神經模型的預測缺乏透明性,人們難以理解[36],而這對于與安全和道德相關的關鍵決策應用至關重要[5]。此外,圖拓撲、節點特征和映射矩陣的耦合導致復雜的預測機制,無法充分利用數據中的先驗知識。
例如,已有研究表明,標簽傳播法采用上述同質性假設來表示的基于結構的先驗,在圖卷積網絡(GCN)[12]中沒有充分使用[15,31]。作為證據,最近的研究提出通過添加正則化[31]或操縱圖過濾器[15,25]將標簽傳播機制納入GCN。他們的實驗結果表明,通過強調這種基于結構的先驗知識可以改善GCN。然而,這些方法具有三個主要缺點:
(1)其模型的主體仍然是GNN,并阻止它們進行更可解釋的預測;
(2)它們是單一模型而不是框架,因此與其他高級GNN架構不兼容;
(3)他們忽略了另一個重要的先驗知識,即基于特征的先驗知識,這意味著節點的標簽完全由其自身的特征確定。為了解決這些問題,我們提出了一個有效的知識蒸餾框架,以將任意預訓練的GNN教師模型的知識注入精心設計的學生模型中。學生模型是通過兩個簡單的預測機制構建的,即標簽傳播和特征轉換,它們自然分別保留了基于結構和基于特征的先驗知識。具體來說,我們將學生模型設計為參數化標簽傳播和基于特征的2層感知機(MLP)的可訓練組合。另一方面,已有研究表明,教師模型的知識在于其軟預測[9]。通過模擬教師模型預測的軟標簽,我們的學生模型能夠進一步利用預訓練的GNN中的知識。
因此,學習的學生模型具有更可解釋的預測過程,并且可以利用GNN和基于結構/特征的先驗知識。我們的框架概述如圖1所示。
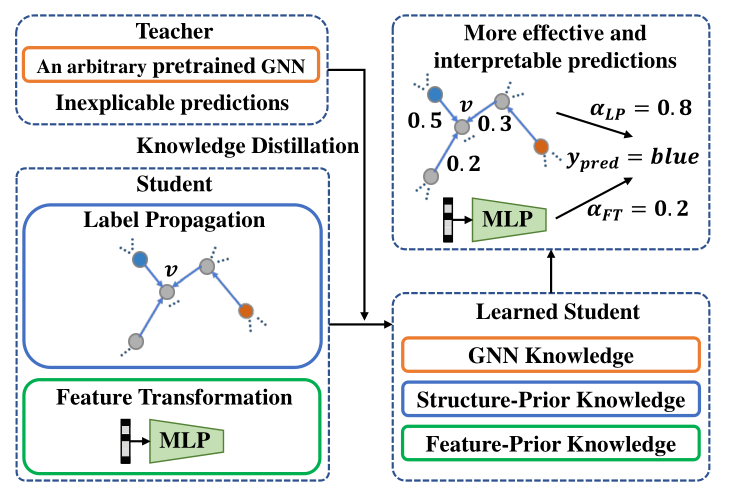
圖1:我們的知識蒸餾框架的示意圖。學生模型的兩種簡單預測機制可確保充分利用基于結構/功能的先驗知識。
在知識蒸餾過程中,將提取GNN教師中的知識并將其注入學生。因此,學生可以超越其相應的老師,得到更有效和可解釋的預測。我們在五個公共基準數據集上進行了實驗,并采用了幾種流行的GNN模型,包括GCN[12]、GAT[30]、SAGE[8]、APPNP[13]、SGC[33]和最新的深層GCN模型GCNII[4]作為教師模型。實驗結果表明,就分類精度而言,學生模型的表現優于其相應的教師模型1.4%-4.7%。
值得注意的是,我們也將框架應用于GLP[15],它通過操縱圖過濾器來統一GCN和標簽傳播。結果,我們仍然可以獲得1.5%-2.3%的相對改進,這表明了我們框架的潛在兼容性。此外,我們通過探究參數化標簽傳播與特征轉換之間的可學習平衡參數以及標簽傳播中每個節點的可學習置信度得分,來研究學生模型的可解釋性。總而言之,改進是一致,并且更重要的是,它具有更好的可解釋性。本文的貢獻總結如下:
我們提出了一個有效的知識蒸餾框架,以提取任意預訓練的GNN模型的知識,并將其注入學生模型,以實現更有效和可解釋的預測。
我們將學生模型設計為參數化標簽傳播和基于特征的兩層MLP的可訓練組合。因此,學生模型有一個更可解釋的預測過程,并自然地保留了基于結構/特征的先驗。因此,學習的學生模型可以同時利用GNN和先驗知識。
五個基準數據集和七個GNN教師模型上的實驗結果表明了我們的框架有效性。對學生模型中學習權重的廣泛研究也說明了我們方法的可解釋性。
2 方法
在本節中,我們將從形式化半監督節點分類問題開始,并介紹符號。然后,我們將展示我們的知識蒸餾框架,以提取GNN的知識。然后,我們將提出學生模型的體系結構,該模型是參數化標簽傳播和基于特征的兩層MLP的可訓練組合。最后,我們將討論學生模型的可解釋性和框架的計算復雜性。
2.1 半監督節點分類
我們首先概述節點分類問題。給定一個連通圖和一個標記點集,其中師節點集,是邊集,節點分類的目標是為每個節點無標記點集中的節點預測標簽。每個節點擁有標簽,其中是所有可能的標簽集合。此外,圖數據通常擁有節點特征,并且可以利用特征來提升分類準確率。每行矩陣的每行表示節點的維特征向量。
2.2 知識蒸餾框架
基于GNN的節點分類方法往往是一個黑盒,輸入圖結構、標記點集和節點特征,輸出分類器。分類器將預測無標記點的標簽為的概率,其中。對于標記節點,如果的標簽為,那么,其余標簽。簡化起見,我們使用表示所有標簽的概率分布。在本文中,我們框架里的教師模型可以使用任意GNN,例如GCN[12]或GAT[30]。我們稱教師模型里的預訓練分類器為。另一方面,我們使用表示學生模型,是參數,表示學生模型對節點v的預測概率分布。在知識蒸餾[9]的框架中,訓練學生模型使其最小化與預訓練教師模型的軟標簽預測,使得教師模型里的潛在知識被提取并注入學生模型中。因此,優化目標是對齊學生模型和與訓練教師模型的輸出,可以形式化為:
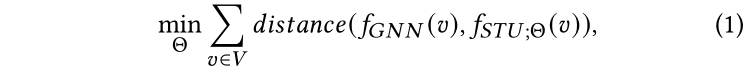
其中度量兩個預測概率分布之間的距離。特別地,本文使用歐氏距離。(注:我們還嘗試最小化KL散度或最大化交叉熵。但是我們發現歐幾里得距離的效果最好,并且在數值上更穩定。)
2.3 學生模型架構
我們假設節點的標簽預測遵循兩種簡單的機制:(1)從其相鄰節點傳播標簽;(2)從其自身特征進行轉換。因此,如圖2所示,我們將學生模型設計為這兩種機制的組合,即參數化標簽傳播(PLP)模塊和特征轉換(FT)模塊,它們可以自然地分別保留基于結構的先驗知識和基于特征的先驗知識。蒸餾后,學生將通過更易于解釋的預測機制從GNN和先驗知識中受益。
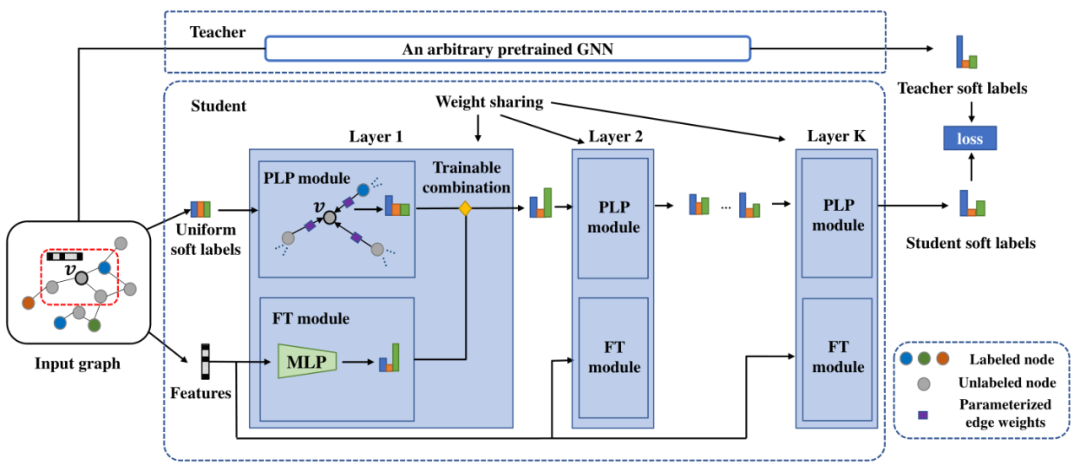
圖2:我們建議的學生模型的架構圖。以中心節點為例,學生模型從節點的原始特征和統一的標簽分布作為軟標簽開始,然后在每一層,將的軟標簽預測更新為來自的鄰居的參數化標簽傳播(PLP)和的特征變換(FT)的可訓練組合。最終,將使學生與經過訓練的教師的軟標簽預測之間的距離最小化。在本小節中,我們將首先簡要回顧傳統的標簽傳播算法。然后,我們將介紹我們的PLP和FT模塊及其可訓練的組合。
2.3.1 標簽傳播
標簽傳播(LP)[40]是基于圖的經典半監督學習模型。該模型僅遵循以下假設:由邊連接(或占據相同流形)的節點極有可能共享相同的標簽。基于此假設,標簽將從標記的節點傳播到未標記的節點以進行預測。正式地,我們使用表示LP的最終預測,使用表示k輪迭代后的LP預測。在這個工作中,如果是標記節點,我們將對節點的預測初始化為一個獨熱編碼向量。否則,我們將為每個未標記的節點設置均勻分布,這表明所有類的概率在開始時都是相同的。初始化可以形式化為:
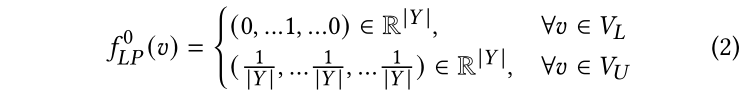
其中,是節點在第次迭代中的預測概率分布。在第k+1次迭代時,LP將按照如下方式更新無標記節點的預測:
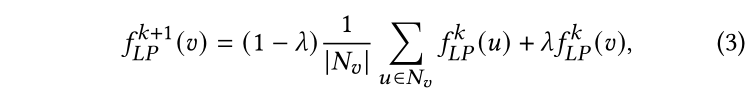
其中,時節點的鄰居集合,是控制節點更新平滑度的超參。注意LP沒有需要訓練的參數,因此以端到端的方式不能擬合教師模型的輸出。因此,我們通過引入更多參數來提升LP的表達能力。
2.3.2 參數化標簽傳播模塊
現在,我們將通過在LP中進一步參數化邊緣權重來介紹我們的參數化標簽傳播(PLP)模塊。如等式3所示,LP模型在傳播過程中平等對待節點的所有鄰居。但是,我們假設不同鄰居對一個節點的重要性應該不同,這決定了節點之間的傳播強度。更具體地說,我們假設某些節點的標簽預測比其他節點更“自信”。例如,一個節點的預測標簽與其大多數鄰居相似。這樣的節點將更有可能將其標簽傳播給鄰居,并使它們保持不變。形式化來說,我們將給每個節點v設置一個置信度分數。在傳播過程中,所有節點的鄰居和自身將把他們的標簽傳播給。基于置信值越大,邊緣權值越大的直覺,我們為重寫了等式3中的預測更新函數如下:
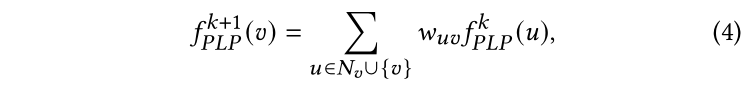
其中是節點和節點的邊權,通過下面的函數計算:
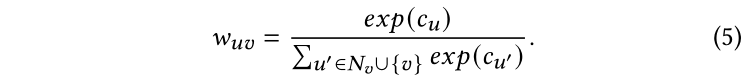
與LP相似,按照等式2初始化,在傳播過程中,每個標記點的仍然保持獨熱真實編碼向量。注意,作為可選項,我們可以進一步參數化置信度分數用于歸納設置:
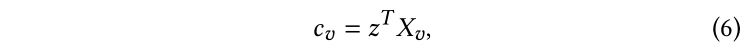
其中,是一個可學習參數,將節點的特征映射為置信度分數。
2.3.3 特征轉換模塊
注意,通過邊緣傳播標簽的PLP模塊強調了基于結構的先驗知識。因此,我們還引入了特征變換(FT)模塊作為補充預測機制。FT模塊僅通過查看節點的原始特征來預測標簽。形式化來說,用表示FT模塊的預測,我們使用兩層MLP后接一個softmax函數來將特征轉換為軟標簽預測:
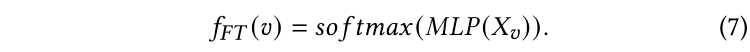
注:雖然單層邏輯回歸更具可解釋性,但我們發現兩層邏輯回歸對于提高學生的模型能力是必要的。
2.3.4 可訓練組合
現在我們將結合PLP和FT模塊作為我們的完整學生模型。細節上,我們將為每個節點學習一個可訓練參數,來平衡PLP和FT之間的預測。換句話說,FT和PLP的預測將在每個傳播步驟合并。我們將合并后的完整模型命名為CPF,等式4中的每個無標記節點的預測更新公式可以重新寫做:
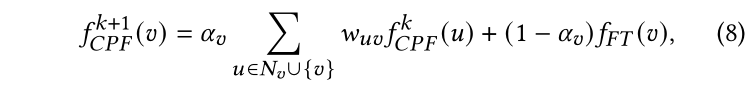
其中邊權和初始化與PLP模塊一致。根據是否按照等式6參數化置信度分數,模型有兩個變體,分別是歸納模型CPF-ind和轉導模型CPF-tra。
2.4 整體算法與細節
假設我們的學生模型一共有K層,等式1中的蒸餾目標可以進一步寫為:
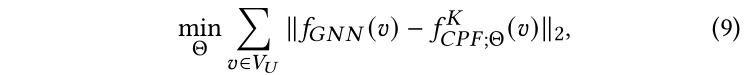
其中,是范數,參數集合包括PLP和FT之間的平衡參數,PLP模塊內部的置信度參數(或歸納設置下的參數),以及FT模塊中MLP的參數。還有一個重要的超參數:傳播層數。
2.5 對模型可解釋性與計算復雜性的討論
在本小節中,我們將討論學習的學生模型的可解釋性和算法的復雜性。經過知識蒸餾后,我們的學生模型CPF會將特定節點的標簽作為標簽傳播和基于特征的MLP的預測之間的加權平均值進行預測。平衡參數指示基于結構的LP還是基于特征的MLP對于節點的預測更重要。LP機制幾乎是透明的,我們可以輕松地找出節點在每個迭代中受哪個鄰居影響的程度。另一方面,對基于特征的MLP的理解可以通過現有工作[21]或直接查看不同特征的梯度來獲得。因此,學習過的學生模型比GNN教師具有更好的解釋性。算法每次迭代(算法1的第3行到第13行)的時間復雜度和空間復雜度都是,這和數據集的規模線性相關。事實上,操作可以簡單寫成矩陣形式,對于真實數據集的訓練過程,使用單GPU可以在幾秒內完成。因此,我們提出的知識蒸餾框架的時間、空間效率都很高。
3 實驗
在本節中,我們將從介紹實驗中使用的數據集和教師模型開始。然后,我們將詳細介紹教師模型和學生變體的實驗設置。之后,我們將給出評估半監督節點分類的定量結果。我們還在不同數量的傳播層和訓練比率下進行實驗,以說明算法的魯棒性。最后,我們將提供定性案例研究和可視化效果,以更好地理解我們的學生模型CPF中的學習參數。
3.1 數據集
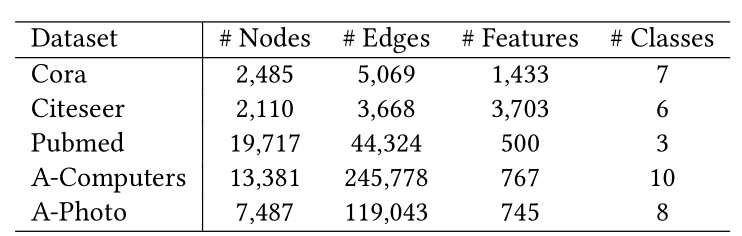
表1:數據集統計信息我們使用五個公共基準數據集進行實驗,數據集的統計數據如表1所示。如以前的文獻[14,24,27]所做的那樣,我們僅考慮最大的連通分量,并將邊視為無向邊。根據先前工作[24]中的實驗設置,我們從每個類別中隨機抽取20個節點作為標記節點,30個用于驗證節點,所有其他節點用于測試。
3.2 教師模型及其設置
為了進行全面比較,我們在我們的知識蒸餾框架中考慮了七個GNN模型作為教師模型;對于每個數據集和教師模型,我們測試下列學生變體:
PLP: 只考慮參數化標簽傳播機制的學生變體;
FT:只考慮特征轉換機制的學生變體;
CPF-ind:歸納設置下的完整模型;
CPF-tra:轉導設置下的完整模型。
3.3 分類結果分析

表2:GCN[12]和GAT[30]作為教師模型的分類準確率

表3:APPNP[13]和SGAE[8]作為教師模型的分類準確率

表4:SGC[33]和GCNII[4]作為教師模型的分類準確率
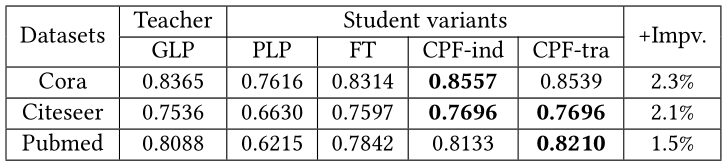
表5:GLP[15]作為教師模型的分類準確率五個數據集、七個GNN教師模型、四個學生變體模型上的實驗結果在表格2,3,4,5中展示。
3.4 不同傳播層數的分析
在本小節中,我們將研究關鍵超參數對學生模型CPF的體系結構(即傳播層數)的影響。實際上,流行的GNN模型(例如GCN和GAT)對層數非常敏感。較大數量的層將導致過平滑的問題,并嚴重損害模型性能。因此,我們在Cora數據集上進行了實驗,以進一步分析該超參數。
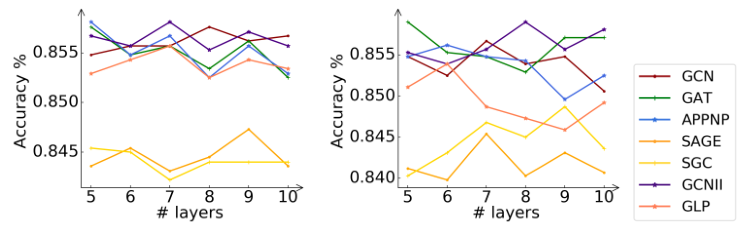
圖3:Cora數據集上具有不同數量傳播層的CPF-ind和CPF-tra的分類精度。圖例表示指導學生的老師模式。
3.5 不同訓練比例的分析
為了進一步證明該框架的有效性,我們在不同的訓練比例下進行了額外的實驗。具體來說,我們以Cora數據集為例,將每個類的標記節點數量從5個變化到50個。實驗結果如圖4所示。
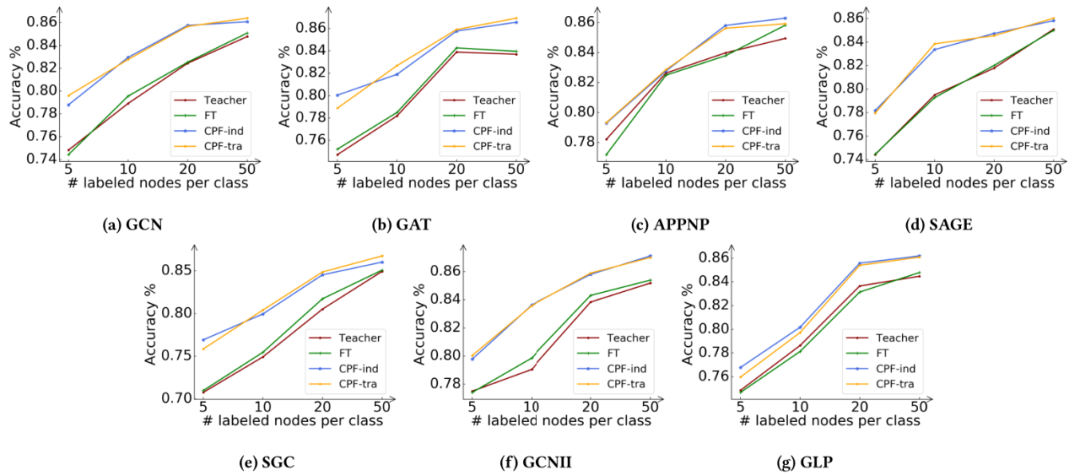
圖4:Cora數據集上不同數量的標記節點下的分類精度。子標題指示相應的教師模型。
3.6 可解釋性分析
現在,我們將分析學習的學生模型CPF的可解釋性。具體來說,我們將探究PLP和FT之間的學習平衡參數以及每個節點的置信度得分。我們的目標是找出哪種節點具有最大或最小的和。在本小節中,我們將使用由GCN和GAT教師模型指導的CPF-ind學生模型在Cora數據集上進行展示。
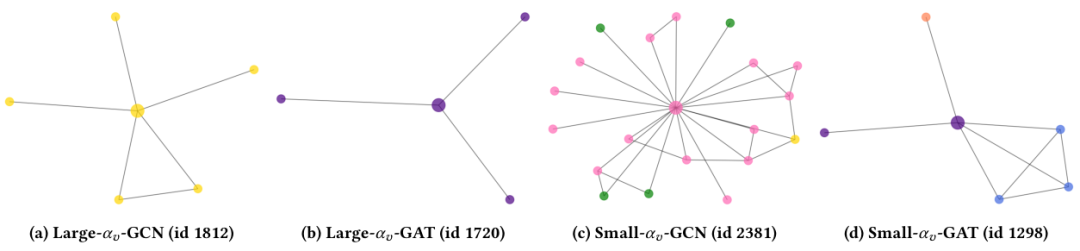
圖5:用于可解釋性分析的平衡參數案例研究。此處的子標題表示該節點是按GCN/GAT作為教師模型,按大或小值選擇的。
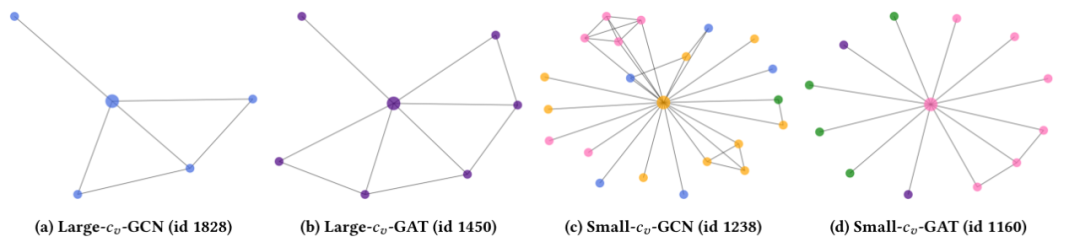
圖6:用于可解釋性分析的置信度得分案例研究。此處的子標題表示該節點是按GCN/GAT作為教師模型,按大或小值選擇的。
4 結論
在本文中,我們提出了一種有效的知識蒸餾框架,可以提取任意預訓練的GNN(教師模型)的知識并將其注入精心設計的學生模型中。學生模型CPF被建立為兩個簡單預測機制的可訓練組合:標簽傳播和特征轉換,二者分別強調基于結構的先驗知識和基于特征的先驗知識。蒸餾后,學習的學生可以利用先驗知識和GNN知識,從而超越GNN老師。在五個基準數據集上的實驗結果表明,我們的框架可以通過更可解釋的預測過程來一致,顯著地改善所有七個GNN教師模型的分類精度。
在不同數量的訓練比率和傳播層數上進行的附加實驗證明了我們算法的魯棒性。我們還提供了案例研究,以了解學生架構中學習到的平衡參數和置信度得分。在未來的工作中,除了半監督節點分類之外,我們還將探索將我們的框架用于其他基于圖的應用。例如,無監督節點聚類任務會很有趣,因為標簽傳播模式在沒有標簽的情況下不能應用。另一個方向是改進我們的框架,鼓勵教師和學生模型互相學習,以取得更好的成績。
原文標題:【WWW2021】圖神經網絡的知識提取與超越:一個有效的知識蒸餾框架
文章出處:【微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉載請注明出處。
責任編輯:haq
-
神經網絡
+關注
關注
42文章
4812瀏覽量
103195 -
深度學習
+關注
關注
73文章
5557瀏覽量
122645
原文標題:【WWW2021】圖神經網絡的知識提取與超越:一個有效的知識蒸餾框架
文章出處:【微信號:zenRRan,微信公眾號:深度學習自然語言處理】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄





 圖神經網絡的知識蒸餾框架介紹
圖神經網絡的知識蒸餾框架介紹











評論