在某些情況下，神經(jīng)網(wǎng)絡(luò)之類模型的表現(xiàn)可能會勝過更簡單的模型，但很多情況下事情并不是這樣的。

打個比方：假設(shè)你需要購買某種交通工具來跑運輸，如果你經(jīng)常需要長距離運輸大型物品，那么， 購買卡車是很劃算的投資；但如果你只是要去本地超市買點牛奶，那么買一輛卡車就太浪費了。一輛汽車（如果你關(guān)心氣候變化的話，甚至可以買一輛自行車）也足以完成上述任務(wù)。

深度學(xué)習(xí)的使用場景也開始遇到這種問題了：我們假設(shè)它們的性能優(yōu)于簡單模型，然后把相關(guān)數(shù)據(jù)一股腦兒地塞給它們。此外，我們在應(yīng)用這些模型時往往并沒有對相關(guān)數(shù)據(jù)有適當(dāng)?shù)睦斫猓槐热缯f我們沒有意識到，如果對數(shù)據(jù)有直觀的了解，就不必進行深度學(xué)習(xí)。

任何模型被裝在黑匣子里來分析數(shù)據(jù)時，總是會存在危險，深度學(xué)習(xí)家族的模型也不例外。

時間序列分析我最常用的是時間序列分析，因此我們來考慮一個這方面的例子。

假設(shè)一家酒店希望預(yù)測其在整個客戶群中收取的平均每日費用（或每天的平均費用）——ADR。每位客戶的平均每日費用是每周開銷的平均值。

LSTM 模型的配置如下：

model = tf.keras.Sequential（）

model.add（LSTM（4， input_shape=（1， lookback）））

model.add（Dense（1））

model.compile（loss=‘mean_squared_error’， optimizer=‘a(chǎn)dam’）

history=model.fit（X_train， Y_train， validation_split=0.2， epochs=100， batch_size=1， verbose=2）

下面是預(yù)測與實際的每周 ADR：

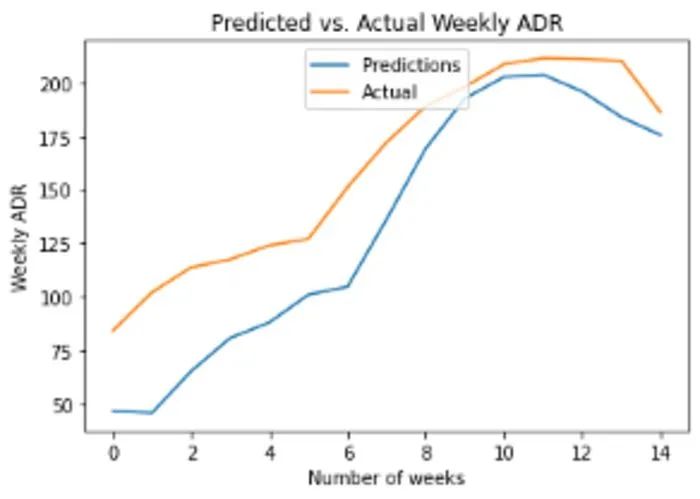
獲得的 RMSE 為 31，均值 160。RMSE（均方根誤差）的大小是平均 ADR 大小的 20％。誤差并不算高，但不得不承認(rèn)，神經(jīng)網(wǎng)絡(luò)的目的是盡可能獲得比其他模型更高的準(zhǔn)確度，所以這個結(jié)果還是有些令人失望。

此外，這個 LSTM 模型是一個一步預(yù)測——意味著如果沒有可用的時間 t 之前的所有數(shù)據(jù)，該模型就無法進行長期預(yù)測。

也就是說，我們是不是太急著對數(shù)據(jù)應(yīng)用 LSTM 模型了呢？

我們先回到出發(fā)點，首先對數(shù)據(jù)做一個全面的分析。

下面是 ADR 波動的 7 周移動平均值：

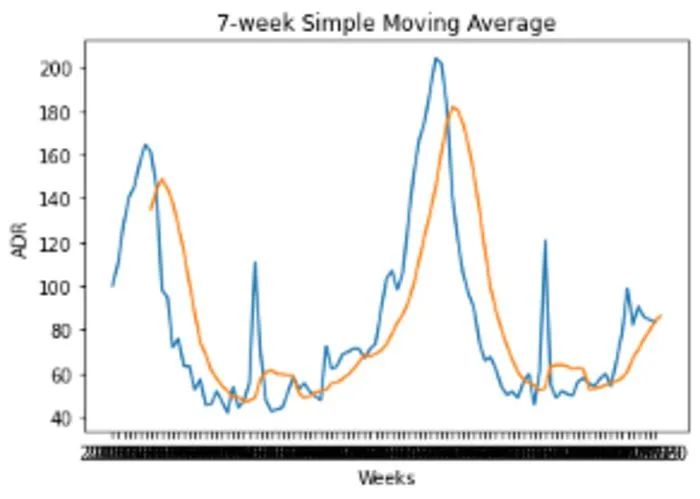
當(dāng)數(shù)據(jù)通過 7 周的移動平均值進行平滑處理后，我們可以清楚地看到季節(jié)性模式的證據(jù)。

我們來仔細(xì)看看數(shù)據(jù)的自相關(guān)函數(shù)。

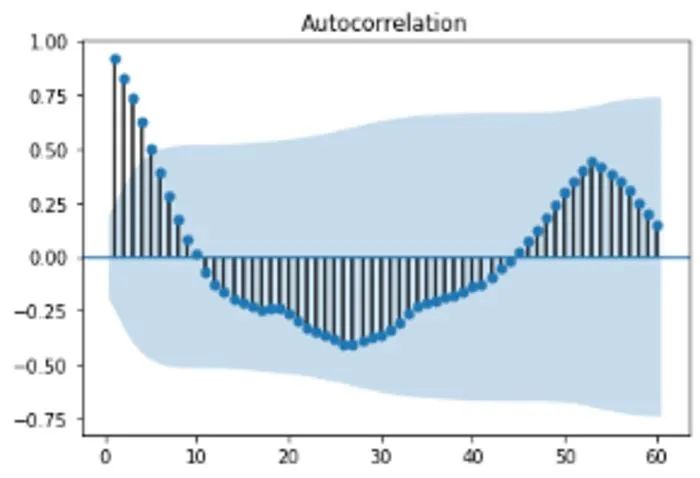
我們可以看到，峰值相關(guān)性（在一系列負(fù)相關(guān)性之后）滯后 52，表明數(shù)據(jù)中存在年度季節(jié)屬性。

有了這一信息后，我們可以使用 pmdarima 配置 ARIMA 模型來預(yù)測 ADR 波動的最后 15 周，并自動選擇 p、d、q 坐標(biāo)以最小化赤池量信息準(zhǔn)則。

》》》 Arima_model=pm.auto_arima（train_df， start_p=0， start_q=0， max_p=10， max_q=10， start_P=0， start_Q=0， max_P=10， max_Q=10， m=52， stepwise=True， seasonal=True， information_criterion=‘a(chǎn)ic’， trace=True， d=1， D=1， error_action=‘warn’， suppress_warnings=True， random_state = 20， n_fits=30）Performing stepwise search to minimize aic

ARIMA（0，1，0）（0，1，0）［52］ ： AIC=422.399， Time=0.27 sec

ARIMA（1，1，0）（1，1，0）［52］ ： AIC=inf， Time=16.12 sec

ARIMA（0，1，1）（0，1，1）［52］ ： AIC=inf， Time=19.08 sec

ARIMA（0，1，0）（1，1，0）［52］ ： AIC=inf， Time=14.55 sec

ARIMA（0，1，0）（0，1，1）［52］ ： AIC=inf， Time=11.94 sec

ARIMA（0，1，0）（1，1，1）［52］ ： AIC=inf， Time=16.47 sec

ARIMA（1，1，0）（0，1，0）［52］ ： AIC=414.708， Time=0.56 sec

ARIMA（1，1，0）（0，1，1）［52］ ： AIC=inf， Time=15.98 sec

ARIMA（1，1，0）（1，1，1）［52］ ： AIC=inf， Time=20.41 sec

ARIMA（2，1，0）（0，1，0）［52］ ： AIC=413.878， Time=1.01 sec

ARIMA（2，1，0）（1，1，0）［52］ ： AIC=inf， Time=22.19 sec

ARIMA（2，1，0）（0，1，1）［52］ ： AIC=inf， Time=25.80 sec

ARIMA（2，1，0）（1，1，1）［52］ ： AIC=inf， Time=28.23 sec

ARIMA（3，1，0）（0，1，0）［52］ ： AIC=414.514， Time=1.13 sec

ARIMA（2，1，1）（0，1，0）［52］ ： AIC=415.165， Time=2.18 sec

ARIMA（1，1，1）（0，1，0）［52］ ： AIC=413.365， Time=1.11 sec

ARIMA（1，1，1）（1，1，0）［52］ ： AIC=415.351， Time=24.93 sec

ARIMA（1，1，1）（0，1，1）［52］ ： AIC=inf， Time=21.92 sec

ARIMA（1，1，1）（1，1，1）［52］ ： AIC=inf， Time=30.36 sec

ARIMA（0，1，1）（0，1，0）［52］ ： AIC=411.433， Time=0.59 sec

ARIMA（0，1，1）（1，1，0）［52］ ： AIC=413.422， Time=11.57 sec

ARIMA（0，1，1）（1，1，1）［52］ ： AIC=inf， Time=23.39 sec

ARIMA（0，1，2）（0，1，0）［52］ ： AIC=413.343， Time=0.82 sec

ARIMA（1，1，2）（0，1，0）［52］ ： AIC=415.196， Time=1.63 sec

ARIMA（0，1，1）（0，1，0）［52］ intercept ： AIC=413.377， Time=1.04 sec

Best model： ARIMA（0，1，1）（0，1，0）［52］

Total fit time： 313.326 seconds

根據(jù)上面的輸出，ARIMA（0，1，1）（0，1，0）［52］ 是 AIC 的最佳擬合模型。使用這個模型，對于 160 的平均 ADR，可獲得 10 的 RMSE。

這比 LSTM 實現(xiàn)的 RMSE 要低得多（這是一件好事），僅占均值大小的 6％多。

對數(shù)據(jù)進行適當(dāng)?shù)姆治龊螅藗儠J(rèn)識到，數(shù)據(jù)中存在的年度季節(jié)屬性可以讓時間序列更具可預(yù)測性，而使用深度學(xué)習(xí)模型來嘗試預(yù)測這種屬性在很大程度上是多余的。

回歸分析：預(yù)測客戶 ADR 值我們換個角度來討論上述問題。

現(xiàn)在我們不再嘗試預(yù)測平均每周 ADR，而是嘗試預(yù)測每個客戶的 ADR 值。

為此我們使用兩個基于回歸的模型：

線性 SVM（支持向量機）

基于回歸的神經(jīng)網(wǎng)絡(luò)

兩種模型均使用以下特征來預(yù)測每個客戶的 ADR 值：

IsCanceled：客戶是否取消預(yù)訂

country：客戶的原籍國

marketsegment：客戶的細(xì)分市場

deposittype：客戶是否已支付訂金

customertype：客戶類型

rcps：所需的停車位

arrivaldateweekno：到達(dá)的星期數(shù)

我們使用平均絕對誤差作為效果指標(biāo)，來對比兩個模型相對于平均值獲得的 MAE。

線性支持向量機這里定義了 epsilon 為 0.5 的 LinearSVR，并使用訓(xùn)練數(shù)據(jù)進行了訓(xùn)練：

svm_reg_05 = LinearSVR（epsilon=0.5）

svm_reg_05.fit（X_train， y_train）

現(xiàn)在使用測試集中的特征值進行預(yù)測：

》》》 svm_reg_05.predict（atest）array（［ 81.7431138 ， 107.46098525， 107.46098525， 。..， 94.50144931，

94.202052 ， 94.50144931］）

這是相對于均值的均值絕對誤差：

》》》 mean_absolute_error（btest， bpred）

30.332614341027753》》》 np.mean（btest）

105.30446539770578

MAE 是均值大小的 28％。讓我們看看基于回歸的神經(jīng)網(wǎng)絡(luò)是否可以做得更好。

基于回歸的神經(jīng)網(wǎng)絡(luò)神經(jīng)網(wǎng)絡(luò)的定義如下：

model = Sequential（）

model.add（Dense（8， input_dim=8， kernel_initializer=‘normal’， activation=‘elu’））

model.add（Dense（2670， activation=‘elu’））

model.add（Dense（1， activation=‘linear’））

model.summary（）

使用的批大小是 150，用 30 個 epoch 訓(xùn)練模型：

model.compile（loss=‘mse’， optimizer=‘a(chǎn)dam’， metrics=［‘mse’，‘mae’］）

history=model.fit（xtrain_scale， ytrain_scale， epochs=30， batch_size=150， verbose=1， validation_split=0.2）

predictions = model.predict（xval_scale）

現(xiàn)在將測試集的特征輸入到模型中，以下是 MAE 和平均值：

》》》 mean_absolute_error（btest， bpred）

28.908454264679218》》》 np.mean（btest）

105.30446539770578

我們看到，MAE 僅僅比使用 SVM 所獲得的 MAE 低一點。因此，當(dāng)線性 SVM 模型顯示出幾乎相同的準(zhǔn)確度時，很難證明使用神經(jīng)網(wǎng)絡(luò)來預(yù)測客戶 ADR 是合適的選項。

無論如何，用于“解釋”ADR 的特征選擇之類的因素比模型本身有著更大的相關(guān)性。俗話說，“進垃圾，出垃圾”。如果特征選取很爛，模型輸出也會很差。

在上面這個例子里，盡管兩個回歸模型都顯示出一定程度的預(yù)測能力，但很可能要么 1）選擇數(shù)據(jù)集中的其他特征可以進一步提高準(zhǔn)確性，要么 2）ADR 的變量太多，對數(shù)據(jù)集中特征的影響太大。例如，數(shù)據(jù)集沒有告訴我們關(guān)于每個客戶收入水平的任何信息，這些因素將極大地影響他們每天的平均支出。

結(jié)論

在上面的兩個示例中我們已經(jīng)看到，使用“更輕”的模型已經(jīng)能夠匹配（或超過）深度學(xué)習(xí)模型所實現(xiàn)的準(zhǔn)確性。

在某些情況下，數(shù)據(jù)可能非常復(fù)雜，需要“從頭開始”在數(shù)據(jù)中使用算法學(xué)習(xí)模式，但這往往是例外，而不是規(guī)則。

對于任何數(shù)據(jù)科學(xué)問題，關(guān)鍵是首先要了解我們正在使用的數(shù)據(jù)，模型的選擇往往是次要的。

可以在此處找到上述示例的數(shù)據(jù)集和 Jupyter 筆記本。
編輯：lyn